
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7 Приклади розв’язання типових задачСодержание книги
Поиск на нашем сайте
Приклад 1 Проаналізувати структурні зміни за наведеними даними (дані умовні) про розподіл споживчих витрат населення регіону за окремі періоди і в цілому за весь час:Структура споживчих витрат населення регіону
Розв’язання: Зміну структури споживчих витрат населення регіону можна дослідити за допомогою лінійного коефіцієнта “абсолютних” структурних зрушень (формула 4.7.3), квадратичного коефіцієнта “абсолютних” структурних зрушень (формула 4.7.4), квадратичного коефіцієнта відносних структурних зрушень (формула 4.7.5) та лінійного коефіцієнта “абсолютних” структурних зрушень за n періодів (формула 4.7.6). Для визначення цих показників зробимо допоміжні розрахунки у табличній формі (див. наступну сторінку). Для розрахунку лінійного коефіцієнта “абсолютних” структурних зрушень (формула 4.7.3) за перший (із 2004 по 2005 рік) і за другий (із 2005 по 2006 рік) періоди використовуємо підсумки стовпчиків 2 і 5 розрахункової таблиці:
За наступний рік “абсолютні” структурні зрушення зменшилися, тобто структура споживчих витрат почала стабілізуватися. Аналогічних висновків можна дійти і за розрахунком квадратичного коефіцієнта “абсолютних” структурних зрушень (розрахунки за формулою 4.7.4 із використанням підсумків стовпчиків 3 і 6 розрахункової таблиці):
Визначимо величину квадратичного коефіцієнта відносних структурних зрушень (формула 4.7.5), використовуючи підсумки стовпчиків 4 і 7 розрахункової таблиці:
Для узагальнюючої оцінки структурних зрушень у досліджуваній сукупності в цілому за весь час використовуємо лінійний коефіцієнт “абсолютних” структурних зрушень за n періодів (формула 4.7.6 із підсумками з стовпчика 8 розрахункової таблиці).
Тема 8 Приклади розв’язання типових задач Приклад 2 Провести порівняльний аналізи динаміки заощаджень населення в двох регіонах країни за умовними даними, наведеними в таблиці:
Розв’язання: При необхідності порівняння характеристик паралельних рядів динаміки явищ, що одночасно розвиваються у часі, попередньо проводять приведення їх до однієї основи, для чого переводять абсолютні показники рівнів кожного ряду у відносні, прийнявши рівень якогось одного періоду за одиницю або за сто (за суттю при цьому розраховуються для кожного ряду базисні коефіцієнти або темпи росту). Представимо результати розрахунку в таблиці. (Для регіону Б зроблені аналогічні розрахунки).
Отримані значення темпів росту свідчать про те, що при взятому за основу рівні 2001 року темпи зростання грошових заощаджень значно вищі в регіоні Б, ніж у регіоні А. Але не завжди результати такі очевидні. Порівняльний аналіз в цілому за весь період часу можна зробити, визначивши середньо річні темпи зростання або приросту по кожному регіону і порівнявши їх, тобто визначити коефіцієнт випередження. Визначаємо для кожного регіону середньо річні темпи зростання, використовуючи формули 4.8.14 і 4.8.15 : регіон А - аналогічний розрахунок виконуємо для регіону Б
В середньому за рік у регіоні А грошові заощадження населення зростали на 2,4 %, а у регіоні Б – на 4,1 %. Розраховуємо коефіцієнт випередження, як співвідношення темпів приросту (або темпів росту)
Тема 9 Приклади розв’язання типових задач Приклад 1
Динаміка виробництва продукції на підприємстві характеризується умовними даними, наведеними в таблиці.
Визначити тенденцію розвитку та встановити її характер, використавши різні методи. Зробити висновки та прогнозні розрахунки на кінець року. Розв’язання
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.125.137 (0.008 с.) |

 проц. пункти;
проц. пункти;  проц. пункти.Таким чином, із 2004 по 2005 рік питома вага окремих видів споживчих витрат населення в середньому змінювалася на 5,6 проц. пункти.
проц. пункти.Таким чином, із 2004 по 2005 рік питома вага окремих видів споживчих витрат населення в середньому змінювалася на 5,6 проц. пункти. проц. пункти;
проц. пункти;  проц. пункти.
проц. пункти. ;
;  .Як свідчать ці розрахунки, за перший рік питома вага кожного виду витрат в середньому змінилася майже на ¼ своєї величини, тоді як за наступний рік – тільки на 1/9.
.Як свідчать ці розрахунки, за перший рік питома вага кожного виду витрат в середньому змінилася майже на ¼ своєї величини, тоді як за наступний рік – тільки на 1/9.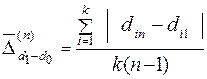 =
=  3,1 проц. пункти.Таким чином, за весь час середньорічна зміна частки споживчих витрат населення регіону за всіма видами витрат становила 3,1 процентних пункти.
3,1 проц. пункти.Таким чином, за весь час середньорічна зміна частки споживчих витрат населення регіону за всіма видами витрат становила 3,1 процентних пункти.
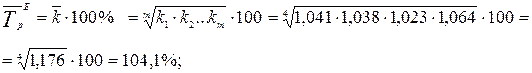
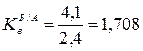 .Таким чином, грошові заощадження населення за період із 2001 по 2006 р. у регіоні Б порівняно із регіоном А зросли у 1,708 рази.
.Таким чином, грошові заощадження населення за період із 2001 по 2006 р. у регіоні Б порівняно із регіоном А зросли у 1,708 рази.


