
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
І. Елементи лінійної алгебриСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклади розв’язання СЛР методом Гаусса
Приклад 1. Розв’язати систему
Розв’язання. Внесемо елементи всіх трьох рівнянь в перші три рядки обчислювальної таблиці 2. Провідний елемент Провідні елементи виділено рамками. Пояснемо деякі результати. В інших клітинах маємо:
Таблиця 2
Аналогічно заповнений рядок 5.
Для рядка 6 маємо у відповідних клітинах:
За даними рядів 1, 4, 6 записуємо трикутну систему
Зворотний хід. Із (Р3) Із (Р2) Із (Р1) Перевірка. Підставимо
Відповідь. Система (11) має єдиний розв’язок:
Приклад 2. Знайти розв’язок системи:
Складаємо обчислювальну таблицю. Таблиця 3
Таблиця 3 заповнюється за викладеною методикою. В 9-му рядку ми отримали нулі. Тепер за даними таблиці 3 запишемо систему рівнянь, в які входять провідні елементи. Сюди включимо формально рівняння з елементами 9-го рядка, отримуємо:
Останнє рівняння вигляду
Далі зворотним ходом знаходимо:
Остаточно:
Рекомендується самостійно переконатись, що співвідношення (16) перетворюють СЛР(13) в тотожності, і отже, є розв’язком цієї системи при довільному значенні Так, наприклад, при При
Прийнято називати розв’язок базисним, якщо при цьому вільні невідомі дорівнюють нулю. Таким чином, система розв’язків (16) дає нескінченну множину розв’язків, якщо вільне невідоме Приклад 3. Знайти розв’язок системи:
Розв’язання. Складаємо обчислювальну таблицю.
Таблиця 4
За результатами таблиці 4 записуємо трикутну систему:
Останнє рівняння із системи (18), Зауваження 1. У викладеній схемі Гаусса ми зупинялись на випадках, коли елементи СЛР цілі числа. Якщо ж ці елементи виражаються десятковими дробами, то в основному поступають так: 1) вибирають серед всіх коефіцієнтів рівняння найбільший за абсолютною величиною (максимальний); 2) ставлять на першому місці в усіх рівняннях доданки з тим невідомим, де міститься цей коефіцієнт; 3)рівняння з максимальним коефіцієнтом переставляють на перше місце; 4)ділять перше рівняння почленно на максимальний коефіцієнт, в результаті провідний елемент стає рівним 1. Дальше застосовують правило прямокутника.
Зауваження 2. На практиці в схемі Гаусса користуються наближеними числами, внаслідок чого виникає похибка, тому ми отримуємо наближені розв’язки
Відхили дають можливість оцінити точність отриманих розв’язків, крім того, можуть використовуватись для знаходження більш точних розв’язків.
Дослідження СЛР за методом Гаусса Із розглянутих прикладів1–3 ми бачимо, що користуючись методом (схемою) Гаусса можна зустрітись із такими випадками: 1) СЛР зводиться до трикутної форми, провiдні елементи якої відмінні від нуля,тоді вона має єдиний розв’язок (приклад 1); 2) СЛР зводиться до трапецієподібної форми, провiдні елементи якої відмінні від нуля,тоді вона має нескінченну множину розв’язків (приклад 2);
3) В СЛР при елементарних перетвореннях з’являється співвідношення
Розв’язати систему лінійних рівнянь
Вправи Обчислити визначники:
Розв’язати рівняння:
Розв’язати подані системи рівнянь та виконати перевірку:
Відповіді:
Методична порада. Якщо ваш час на розв’язання і перевірку (без допомоги калькулятора) однієї системи вигляду 10 – 15 становить більше 5 хвилин, то пропонуємо самостійно скласти і розв’язати ще декілька подібних систем (при змінних – одноцифрові коефіцієнти з різними знаками). Навики обчислення без калькулятора допоможуть вам легше і швидше вивчити наступний матеріал.
1.3. Визначники 3-го порядку. Означення. Оновні властивості
Означення: Визначником 3-го порядку називається число, отримане з дев’яти заданих чисел, розміщених у вигляді квадратної таблиці, обчислене за правилом:
Елементи визначника 3-го порядка розміщені в трьох рядках і трьох стовпцях. Якщо ввести позначення загального елемента Із (1) видно, що кожний член визначника містить по одному і тільки по одному елементу з кожного рядка і кожного стовпця. Обчислювати визначник можна за допомогою правила трикутників, яке зобразимо схематично:
Члени визначника із елементів головної діагоналі, а також члени із елементів, що знаходяться у вершинах трикутників, що мають по одній стороні, паралельній головній діагоналі (ліва схема), беруться із знаком «+», а члени визначника із елементів побічної діагоналі, а також із елементів, що знаходяться у вершинах трикутників, які мають сторони, паралельні побічній діагоналі (права схема) беруться із знаком «-». Розглянемо основні властивості визначників 3-го порядку. 1. Величина визначника не зміниться при заміні відповідних рядків стовпцями (така заміна називається транспонуванням).
2. Знак визначника зміниться на протилежний, якщо в ньому поміняти місцями два його рядки (стовпці). Властивості 1, 2 рекомендується перевірити самостійно згідно з формулою (1). 3. Визначник дорівнює нулю, якщо в ньому однаковими є відповідні елементи двох рядків (стовпців). Дійсно, нехай, наприклад, у визначнику однакові елементи І-го і ІІ-го стовпців:
Помінявши місцями рівні стовпці, ми за властивістю 2 отримаємо новий визначник 4. Визначник дорівнює нулю, якщо всі елементи одного рядка (стовпця) є нулями. Це твердження випливає з того, що кожний член визначника за формулою (1) містить по одному і тільки по одному елементу із кожного рядка і кожного стовпця. В даному випадку по одному елементу з рядка (стовпця), що містить нулі. 5. Спільний множник елементів одного рядка (стовпця) можна винести за знак визначника.
Наприклад,
Перевірити безпосереднім обчислюванням за (1). 6. Якщо елементи одного рядка (стовпця) визначника пропорційні відповідним елементам другого рядка (стовпця), то такий визначник дорівнює нулю. Дійсно, за властивістю 5 коефіцієнт прапорційності можна винести за знак визначника, а тоді скористатись властивістю 3. 7. Якщо кожний з елементів рядка (стовпця) визначника є сумою двох доданків, то цей визначник можна подати у вигляді суми відповідних визначників, наприклад,
Для перевірки досить записати в розгорнутому вигляді за (1) визначник, що в лівій частині рівності, тоді окремо згрупувати члени, що містять елементи 8. Значення визначника не зміниться, якщо до елемента одного рядка (стовпця) додати відповідні елементи другого рядка (стовпця), помножені на одне й теж число. Наприклад,
Ця рівність випливає із властивостей 6 і 7. Приклади 1. Обчислити визначник
2. Перевірити першу властивість визначника
За допомогою властивостей знайти значення визначників
Відповіді. 1) -63. 2) -44. 3) 35. 4) -35. 5) 17. 6) 21. Приклад Для визначника
а) Знайти алгебраїчні доповнення всіх його елементів. б) Перевірити теорему про розклад для всіх трьох стовпців. в) Перевірити теорему про анулювання для алгебраїчних доповнень елементів І-го рядка та відповідних елементів ІІ-го рядка, а тоді для елементів ІІІ-го рядка. Розв’язання а)
б)
в)
Вправи Відповіді
12. 13. 17.
Приклад. Перевірка.
Відповідь: Приклади. За формулами Крамера розв’язати системи рівнянь, у відповідь записати суму коренів.
Відповіді: 1. 8; 2. –2; 3. –6; 4. –2.
Визначники вищих порядків
Розглянемо записаний спочатку формально визначник 4-го порядку:
Викреслюючи в
Нехай введено поняття визначника
можна зобразити, як розклад за елементами першого стовпця:
де Зауваження. Всі властивості 1-8, а також теореми розглянуті для визначників 3-го порядку поширюються і на визначники вищих порядків. Приклад. Обчислити визначник
Розв'язання. Спочатку за допомогою властивості 8 із 1.3 перетворимо в нулі елементи 1-го стовпця, які належать до 2-го 3-го і 4-го рядків. Для цього додамо відповідні елементи 1-го і 2-го рядків. На місці елемента а 21 отримаємо 0 (1+(-1)), а 22=-2+3=1, а 23=(-1)+(-1)=-2, а 24=3+(-1)=2. Щоб отримати 0 в 3-му рядку 1-го стовпця, домножимо на (-3) елементи 1-го рядка і додамо до відповідних елементів 3-го рядка: а 31=1•(-3)+3=0, а 32=(-2)(-3)+(-8)=-2, а 33=(-1)(-3)+7=10, а 34=3•(-3)+7=-2. Домножимо елементи 1-го рядка на (-2) і додамо до відповідних елементів 4-го рядка. Маємо а 41=1•(-2)+2=0, а 42=(-2)•(-2)+1=5, а 43=(-1)(-2)+(-10)=-8, а 44=3(-2)+17=11. Початковий визначник ∆ внаслідок зроблених перетворень має вигляд:
Далі розкладаємо останній визначник за елементами 1-го стовпця. Оскільки а11=1, а решта елементів 1-го стовпця нулі, то отримаємо один визначник 3-го порядку, до якого теж в подальшому застосуємо аналогічні перетворення. В результаті запишемо:
Зауваження. Виконані перетворення в нулі елементів 1-го стовпця, що відносились до 2-го – 4-го рядків, є по суті застосуванням правила прямокутника(див. в 1.1) при перетворенні 2-го – 4-го рядків початкового визначника з провідним елементом 1(1-й рядок, 1-й стовпець). Приклади. Обчислити визначники.
Відповіді. 1. 3; 2. 28; 3. 12; 4. 84.
Прямокутника Приклади Обчислити визначники:
Відповіді:
Лінійні дії над матрицями
Іноді в роботі з таблицями (матрицями) прикладів типу 1–3 із 1.8., доводиться виконувати над ними певні операції. Так, якщо в прикладі 1 потрібно підрахувати заплановий розмір стипендій за семестр (6 місяців), то очевидно необхідно кожний елемент цієї матриці помножити на 6. Виникає необхідність множити матрицю на число. Якщо в умовах прикладу 2 ми маємо відомості 3-х місяців одного квартала, то можна скласти зведену відомість за квартал, додаючи розміщені у відповідних графах дані стосовно кожного робітника. Приходимо до дії додавання матриць. Якщо в умовах прикладу 3, 1.8. позначити через
Отже з прикладів бачимо, що цілком природно виникає необхідність дій множення матриці на число і додавання матриць. Означення 1. Добутком числа
Матриця (–1) Дія додавання вводиться тільки для матриць одного і того ж розміру. Означення 2. Сумою двох матриць
Якщо ж Дії додавання, віднімання і множення матриць на число називаються лінійними діями над матрицями. Можна перевірити, що вони мають такі властивості:
Тут позначено через 0 – нульову матрицю і Вправа. Перевірити властивості 1–8 для матриць
і чисел Приклад. Задані матриці
Знайти 1) Розв’язання. 1)
2) Множення матриць
Множення матриць розглянемо, починаючи з відомого вже прикладу 3, при підрахунку грошових затрат на виконання робіт по проходці в шахті (метро, тунелі). Нехай в рядках матриці
записані результати роботи за добу кожної із трьох змін: по виїмці породи (перший стовпець) і по кріпленню пройденої виробки (другий стовпець). Як вже згадувалось, при заданій площі поперечного перетину проходки результати робіт можуть вимірюватись в пройденних погонних метрах. Замовнику необхідно знати, яку суму грошей прийдеться виділяти на оплату праці робітників, а яку – на капітальні витрати. Існують норми розцінок на зарплату і капітальні витрати, які представимо у вигляді матриці розцінок
де перший стовпець Загальні затрати на зарплату для кожної із змін дорівнюють сумі добутків пройдених кількостей метрів по обох видах робіт на відповідні норми розцінок. Позначимо через
Отримаємо таблицю затрат
Ці дані запишемо у вигляді нової матриці затрат
Для множення матриці Означення 1. Добутком матриці
Із структури елементів Приклад 1. Знайти добуток матриць Розв’язання. Матриця
Приклад 2. Переконатись, що для даних матриць
Звернути увагу, що в даному випадку Приклад 3. Переконатись, що для даних матриць
Звернути увагу, що добуток двох ненульових матриць може давати нульову матрицю, і, крім того, Означення 2. Матриці Приклад 4.
Легко перевірити, що довільна квадратна і одинична матриці комутативні, і при цьому Приклад 5. Перевірити останню рівність, якщо
Можна показати, що множення матриць має такі властивості:
Тут мається на увазі, що всі записані добутки матриць існують. Приклад 6. Перевірити властивості 1-4, якщо число
Розглянемо поняття степеня квадратної матриці. Означення 3. Квадратом матриці Аналогічно вводиться Приклад 7. Для матриць
довести, що Означення 4. Якщо
де Приклад 8. Для матриці
Знайти Обчислити степені квадратних матриць: 9. 12. Перемножити прямокутні матриці: 15. 17. Знайти
Відповіді.
10. |


 . Рядки 4 і 5 заповнюємо згідно з перетворенням за правилом прямокутника елементів 2-го і 3-го рядків.
. Рядки 4 і 5 заповнюємо згідно з перетворенням за правилом прямокутника елементів 2-го і 3-го рядків.





 5
5




 стане провідним елементом,
стане провідним елементом,
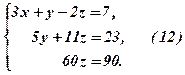

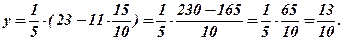
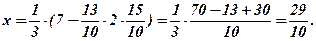
 в СЛР(11), одержимо:
в СЛР(11), одержимо:
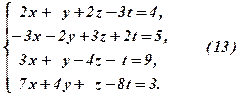



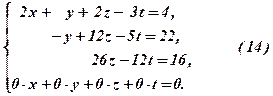
 відкидаємо. Система (14) має трапецієподібну форму. Запишемо її в трикутній формі, для чого перенесемо в праві частини доданки з невідомим
відкидаємо. Система (14) має трапецієподібну форму. Запишемо її в трикутній формі, для чого перенесемо в праві частини доданки з невідомим 



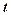 , яке називають вільним невідомим, а
, яке називають вільним невідомим, а  прийнято називати базисними невідомими.
прийнято називати базисними невідомими. розв’язком буде:
розв’язком буде: 


 -2
-2


 , розв’язку немає, отже і вся система (18), а, значить, і еквівалентна їй система (17) теж розв’язку немає, тобто несумісна.
, розв’язку немає, отже і вся система (18), а, значить, і еквівалентна їй система (17) теж розв’язку немає, тобто несумісна. . Це, наприклад, для системи трьох рівнянь з трьома невідомими. Різниця між лівою частиною рівняння при
. Це, наприклад, для системи трьох рівнянь з трьома невідомими. Різниця між лівою частиною рівняння при 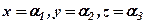 і правою частиною називається відхилом, позначається:
і правою частиною називається відхилом, позначається:
 де
де  . В цьому випадку СЛР розв’язків немає, вона несумісна (приклад 3).
. В цьому випадку СЛР розв’язків немає, вона несумісна (приклад 3).


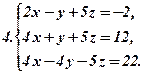












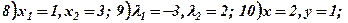



 Приклад. За допомогою формули (1) обчислити визначник
Приклад. За допомогою формули (1) обчислити визначник
 .
. , то перший індекс означає номер рядка, а другий з індексів - номер стовпця. Розрізняють головну (елементи
, то перший індекс означає номер рядка, а другий з індексів - номер стовпця. Розрізняють головну (елементи  ) і побічну (елементи
) і побічну (елементи  ) діагоналі визначника. Доданки в правій частині (1) називаються членами визначника.
) діагоналі визначника. Доданки в правій частині (1) називаються членами визначника.



 . З іншого боку новий визначник збігається з початковим оскільки рівні відповіді елементи, тобто
. З іншого боку новий визначник збігається з початковим оскільки рівні відповіді елементи, тобто  . З цих рівностей маємо:
. З цих рівностей маємо:  . Такий же результат можна отримати безпосереднім обчисленням.
. Такий же результат можна отримати безпосереднім обчисленням.

 . Кожна з отриманих груп доданків буде відповідно першим і другим визначником із правої частини рівності.
. Кожна з отриманих груп доданків буде відповідно першим і другим визначником із правої частини рівності.









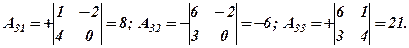 Часто подібні результати зручно записувати у вигляді таблиці (матриці):
Часто подібні результати зручно записувати у вигляді таблиці (матриці):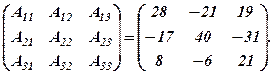








 . Вказівка. Відняти останній стовпець від перших двох.
. Вказівка. Відняти останній стовпець від перших двох.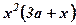 . Вказівка. Відняти від першого стовпця другий, а від другого третій. 14.
. Вказівка. Відняти від першого стовпця другий, а від другого третій. 14.  . Вказівка. Відняти від першого рядка другий, від другого третій. 15.
. Вказівка. Відняти від першого рядка другий, від другого третій. 15.  . Вказівка. До третього стовпця додати другий. 16.
. Вказівка. До третього стовпця додати другий. 16.  .
. .
.
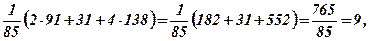





 і-тий рядок і j-тий стовпець, на перетині яких міститься елемент
і-тий рядок і j-тий стовпець, на перетині яких міститься елемент  , отримаємо визначник 3-го порядку, який називається мінором елемента
, отримаємо визначник 3-го порядку, який називається мінором елемента  і позначається
і позначається  . Тоді
. Тоді  - алгебраїчне доповнення елемента
- алгебраїчне доповнення елемента 
 -го порядку, тоді визначник
-го порядку, тоді визначник  -го порядку:
-го порядку: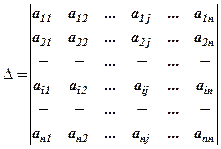

 - алгебраїчні доповнення, а
- алгебраїчні доповнення, а  - мінори елементів першого стовпця. Останні є визначниками
- мінори елементів першого стовпця. Останні є визначниками  -го порядку.
-го порядку. .
. .
.
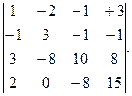


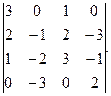
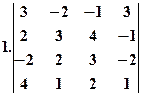 .
.  .
.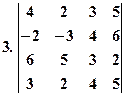 .
.  .
.
 і
і 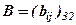 – результати роботи 3-х змін за першу і другу добу відповідно, то можна знайти сумарні результати за дві доби додаванням відповідних елементів і позначити це
– результати роботи 3-х змін за першу і другу добу відповідно, то можна знайти сумарні результати за дві доби додаванням відповідних елементів і позначити це
 на матрицю
на матрицю  розміру
розміру 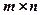 називається нова матриця
називається нова матриця 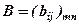 того ж розміру, кожний елемент якої дорівнює відповідному елементу матриці
того ж розміру, кожний елемент якої дорівнює відповідному елементу матриці 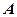 помноженному на число
помноженному на число 
 .
. того ж розміру, кожний елемент якої дорівнює сумі відповідних елементів матриць–доданків, тобто
того ж розміру, кожний елемент якої дорівнює сумі відповідних елементів матриць–доданків, тобто  , і позначається
, і позначається 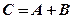 .
. , то
, то  — різниця матриць.
— різниця матриць.
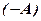 — протилежну матриці
— протилежну матриці 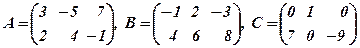
 .
.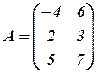 ,
,  .
.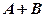 ; 2)
; 2)  .
.
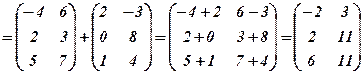 .
.
 .
.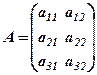
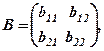
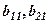 – норми оплати праці робітників: за 1 погонний метр по виїмці породи і за 1 погонний метр по кріпленню відповідно. Другий стовпець:
– норми оплати праці робітників: за 1 погонний метр по виїмці породи і за 1 погонний метр по кріпленню відповідно. Другий стовпець:  – відповідні капітальні затрати за 1 погонний метр виїмки і за 1 погонний метр кріплення.
– відповідні капітальні затрати за 1 погонний метр виїмки і за 1 погонний метр кріплення. сумму грошей зароблену
сумму грошей зароблену  -ю зміною
-ю зміною 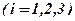 . Аналогічно підраховуються капітальні затрати
. Аналогічно підраховуються капітальні затрати  для
для 
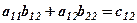
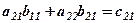


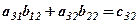
 , що отримана з матриць
, що отримана з матриць 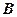 за допомогою операції, яку називають множенням матриць, і позначають
за допомогою операції, яку називають множенням матриць, і позначають
 на матрицю
на матрицю  необхідна їх узгодженність, тобто, щоб число стовпців матриці
необхідна їх узгодженність, тобто, щоб число стовпців матриці  розміру
розміру  , елементи якої
, елементи якої 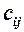 дорівнюють сумі добутків елементів
дорівнюють сумі добутків елементів  -того рядка матриці
-того рядка матриці  -того стовпця матриці
-того стовпця матриці 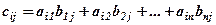 .
.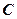 дорівнює числу рядків першого співмножника, а число стовпців- числу стовпців другого співмножника.
дорівнює числу рядків першого співмножника, а число стовпців- числу стовпців другого співмножника. і
і  , якщо
, якщо  ,
,  .
. розміром 2х3, тобто
розміром 2х3, тобто

 .
.
 .
.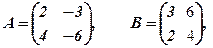

 .
.
 .
.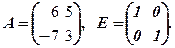
 де
де  .
. , а матриці
, а матриці 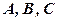 такі:
такі: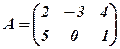 ,
, 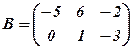 , С=
, С= 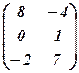 .
.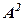 ) називається добуток
) називається добуток  , тобто
, тобто  .
. .
. ,
,  ,
,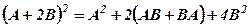 , та знайти значення виразів.
, та знайти значення виразів. - заданий многочлен і
- заданий многочлен і 
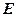 - одинична матриця, називається многочленною матрицею.
- одинична матриця, називається многочленною матрицею.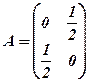
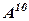
 . 10
. 10  . 11.
. 11.  .
. . 13.
. 13. 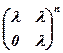 . 14.
. 14. 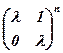 .
.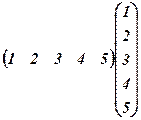 . 16.
. 16.  .
.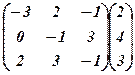 .
. , якщо задана матриця
, якщо задана матриця 
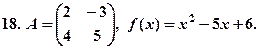
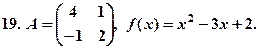
 8.
8. 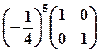 . 9.
. 9.  .
.


