
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наведемо ще один, як на нашу думку новий спосіб обчислення визначників, що ґрунтується на правилі прямокутника. Тут істотно застосовується властивість 8, що розглядалась в 1. 3Содержание книги
Поиск на нашем сайте
Значення визначника не зміниться, якщо до елементів одного рядка (стовпця) додати відповідні елементи другого рядка (стовпця), помножені на одне і те ж число. Особливо зручною стає ця властивість тоді, коли серед елементів рядка (стовпця), які множаться на число є такий, що дорівнює 1. Цей елемент вважають провідним, тоді решту елементів рядка (стовпця), за допомогою властивості 8 можна перетворити в нулі, в результаті чого можна знизити порядок визначника. Виклад суті згаданого способу почнемо з визначника ІІ-го порядку. Отже, нехай дано
Домножимо елементи І-го рядка на
де
Застосуємо подібні перетворення для обчислення визначників ІІІ-го порядку
Згідно з властивістю визначників 8 домножимо елементи І-го рядка на
де елементи За співвідношенням (1) для мінора, що входить в останній визначник (2), маємо
де Отже, останній визначник із рівності (2) зводиться до трикутного вигляду, тобто в результаті маємо таку послідовність перетворень за правилом прямокутника
Для визначника 4-го порядку послідовність основних перетворень за правилом прямокутника має такий вигляд
Очевидно, що при переході до визначника вищого порядку, наприклад, 5-го, ми можемо за правилом прямокутника і властивістю 8 утворити в першому стовпці, крім
Тепер подамо алгоритм обчислення визначників за правилом прямокутника 1. Елемент 2. Перед визначником ставимо співмножник 3. Елементи першого стовпця, що лежать нижче елемента 4. Наступним провідним елементом вибираємо по діагоналі 5. Вводимо в поправочний коефіцієнт співмножник 6. Замінюємо елементи ІІ-го стовпця, що лежать нижче 7. Процес перетворення продовжується поки не зведемо визначник до трикутної форми. 8. Знайдений добуток діагональних елементів скорочуємо з поправочними коефіцієнтами. Зауваження. Описаний алгоритм у випадку дробових, або багатоцифрових елементів надійніше виконувати з застосуванням контролю, як це викладено в (1.1) Приклад 1. Обчислити визначник: а) за алгоритмом; б) за допомогою обчислювальної таблиці з контролем.
а)
б) Обчислювальна таблиця
За даними таблиці отримуємо визначник трикутного вигляду разом з поправочним коефіцієнтом
Приклад 2. Обчислити визначник
Обчислювальна таблиця
Приклади Обчислити визначники:
Відповіді:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.4.52 (0.009 с.) |

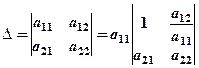 .
.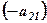 і почленно додамо до ІІ-го рядка.
і почленно додамо до ІІ-го рядка.
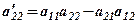 - знайдено за правилом прямокутника (див. 1.1). Таким чином, ми звели визначник до трикутної форми, і його значення дорівнює добутку діагональних елементів та коефіцієнта
- знайдено за правилом прямокутника (див. 1.1). Таким чином, ми звели визначник до трикутної форми, і його значення дорівнює добутку діагональних елементів та коефіцієнта 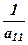 , тобто
, тобто (1)
(1)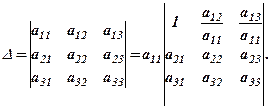
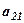 отримаємо
отримаємо  . Аналогічно, знову домножимо елементи І-го рядка на
. Аналогічно, знову домножимо елементи І-го рядка на  і додамо до відповідних елементів ІІІ-го рядка. На місці
і додамо до відповідних елементів ІІІ-го рядка. На місці  - теж
- теж 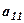 знову введемо в І-ий рядок, тоді
знову введемо в І-ий рядок, тоді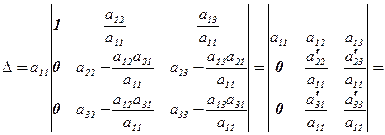
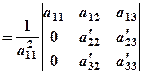 (2)
(2)
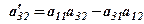 .
. 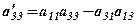 - знайдені за правилом прямокутника (див. 1.1).
- знайдені за правилом прямокутника (див. 1.1).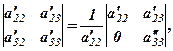
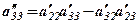 , при цьому вважається, що
, при цьому вважається, що 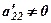 .
.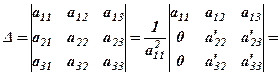
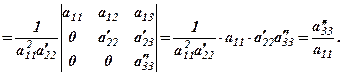 (3)
(3)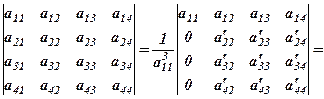
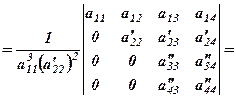
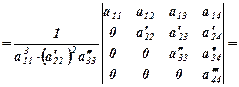
 (4)
(4)
 , нулі і звести задачу до обчислення визначника 4-го порядку.
, нулі і звести задачу до обчислення визначника 4-го порядку.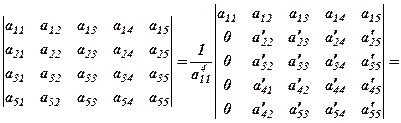

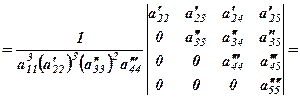
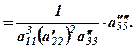 (5)
(5)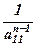 , де
, де 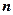 - порядок визначника, назвемо його поправочним коефіцієнтом. Значення показника степеня
- порядок визначника, назвемо його поправочним коефіцієнтом. Значення показника степеня  збігається з кількістю нулів, які будуть стояти в першому стовпці нижче елемента
збігається з кількістю нулів, які будуть стояти в першому стовпці нижче елемента 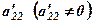 .
.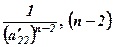 - кількість нулів, що будуть після
- кількість нулів, що будуть після 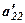 у другому стовпці.
у другому стовпці.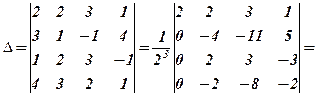
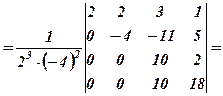

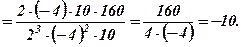

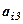


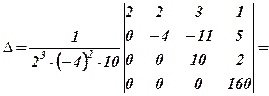



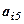
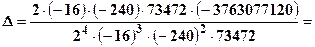
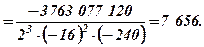
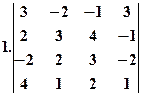 .
.  .
.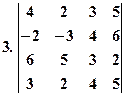 .
.  .
.



