
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм нахождения обратной матрицыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Составим алгоритм нахождения обратной матрицы с использованием равенства
Свойства Обратной матрицы Понятие обратной матрицы, равенство
13. Ранг матрицы. Свойства ранга матрицы. Элементарные преобразования матрицы. Ранг матрицы Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля. Свойства ранга матрицы 1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы. 2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец. Элементарные преобразования матрицы 1) умножение какой-нибудь строки (столбца) на отличное от нуля число; 2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число; 3) перестановку местами любых двух строк (столбцов).
14. Системы линейных уравнений. Однородные и неоднородные системы. Совместность системы. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно. Однородные системы
всегда является совместной. Доказательство. Для этой системы набор чисе
В этом разделе мы будем использовать матричную запись системы: Предложение 15.3 Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением. Доказательство. Пусть
Так как Пусть
Так как
Следствие 15.1 Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений. Действительно, умножая ненулевое решение на различные числа, будем получать различные решения. Определение 15.5 Будем говорить, что решения Определение 15.6 Пусть
где Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях Как находить фундаментальную систему решений мы увидим позже, в разделе "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)". Теорема 15.3 Пусть Неоднородные системы Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно n неизвестных
В отличие от однородной системы, эта система совместна не всегда. Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
15. Метод Крамера для нахождения решения системы линейных уравнений. Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод. Для системы
с определителем матрицы системы
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В этой форме формула Крамера справедлива без предположения, что
16. Матричный метод решения систем линейных уравнений. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем. Пусть дана система линейных уравнений с
Тогда её можно переписать в матричной форме:
Умножим это матричное уравнение слева на Так как
Для однородной системы линейных уравнений, то есть когда вектор
17. Метод Гаусса для нахождения решения системы линейных уравнений. Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Решение. Выпишем расширенную матрицу данной системы и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: б) третью строку умножим на (-5) и прибавим к ней вторую: В результате всех этих преобразований данная система приводится к треугольному виду: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13. Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим
18. Понятие вектора. Линейные операции над векторами. Вектором (в реальном пространстве) называется направленный отрезок
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.134.140 (0.011 с.) |

 .
. - матрицу из алгебраических дополнений элементов
- матрицу из алгебраических дополнений элементов  .
. .
. . Этой операцией завершается нахождение обратной матрицы
. Этой операцией завершается нахождение обратной матрицы  .
.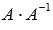 и
и  . Если
. Если  , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.
, то обратная матрица найдена верно, в противном случае где-то была допущена ошибка. .
. .
. .
. .
.

 ,
,  ,
,  ,
, 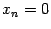 является решением.
является решением. .
. и
и  служат решениями системы
служат решениями системы 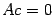 и
и  . Пусть
. Пусть  . Тогда
. Тогда
 , то
, то  -- решение.
-- решение.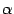 -- произвольное число,
-- произвольное число, 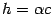 . Тогда
. Тогда
 , то
, то  -- решение.
-- решение. системы
системы 
 -- произвольные числа, будем называть общим решением системы
-- произвольные числа, будем называть общим решением системы  , где
, где  -- число неизвестных в системе.
-- число неизвестных в системе.
 линейных уравнений с
линейных уравнений с 
 , отличным от нуля, решение записывается в виде
, отличным от нуля, решение записывается в виде

 и
и  , либо набор
, либо набор 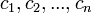 состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама иЛеммы Накаямы.
состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама иЛеммы Накаямы.
 , где
, где  — основная матрица системы,
— основная матрица системы,  и
и  — столбцы свободных членов и решений системы соответственно:
— столбцы свободных членов и решений системы соответственно: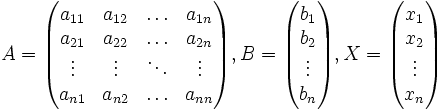
 — матрицу, обратную к матрице
— матрицу, обратную к матрице 
 , получаем
, получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: .
.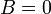 , действительно обратное правило: система
, действительно обратное правило: система 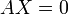 имеет нетривиальное (то есть ненулевое) решение только если
имеет нетривиальное (то есть ненулевое) решение только если 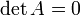 . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
 ;
;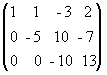 .
. с начальной точкой
с начальной точкой 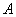 и конечной точкой
и конечной точкой  , который можно передвигать параллельно самому себе. Таким образом, считается, что два направленных отрезка
, который можно передвигать параллельно самому себе. Таким образом, считается, что два направленных отрезка  , имеющие равные длины (
, имеющие равные длины (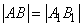 ) и одно и то же направление, определяют один и тот же вектор
) и одно и то же направление, определяют один и тот же вектор  , и в этом смысле пишут
, и в этом смысле пишут 



