
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Промежутки монотонности функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Промежутки монотонности функции Говорят, что функция Другими словами, функция Чтобы по графику функции Говорят, что функция Другими словами, функция Чтобы по графику функции Точки максимума и минимума функции. Точка
Графически это означает что точка с абсциссой Точка
Графически это означает что точка с абсциссой Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной. Четность (нечетность) функции. Функция а) Для любого значения аргумента Другими словами, область определения четной функции б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение
Функция а) Для любого значения аргумента Другими словами, область определения нечетной функции б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида. Чтобы определить четность функции, нужно: а). Найти область определения функции Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция Если область определения функции б). В уравнение функции Если Если Если не удалось привести ни к тому ни к другому, то наша функция График четной функции симметричен относительно оси ординат (прямой OY). График нечетной функции симметричен относительно начала координат (точки (0,0)). Периодичность функции. Функция § для любого значения х из области определения функции, х+Т также принадлежит D(x) § В программе средней школы из числа периодических функций изучают только тригонометрические функции. Предлагаю вам посмотреть ВИДЕОРОК, в котором я рассказываю, как определить свойства функции, график которой изображен на рисунке: Обратная функция
Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:
v = u 2,
где u - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v:
Если обозначить аргумент в обеих функциях через x, а функцию – через y, то мы имеем две функции:
каждая из которых является обратной по отношению к другой. Сложная функция – функция от функции. Если z – функция от у, т.е. z (y), а у, в свою очередь, – функция от х, т.е. у (х), то функция f (x) = z (y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х. В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z (y). Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:
Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f 1(y 1), y 1 = f 2(y 2), …, yn -1 = fn (x), то
28. Понятие числовой последовательности. Арифметические операции над последовательностями. Числовой последовательностью называется бесконечное множество чисел (элементов), имеющих определенные номера. Эти числа являются членами последовательности: x 1-первый член, x 2-второй член,..., x n- n -ый член. Числовая последовательность обозначается так: { x n}. Числовую последовательность задают формулой n -го члена: x n= f (n). Например, если то x1 =2, Числовую последовательность также можно задать рекуррентным соотношением: Тогда
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.5.88 (0.01 с.) |

 – это такие промежутки значений аргумента х, при которых функция
– это такие промежутки значений аргумента х, при которых функция  , принадлежащих промежутку I таких, что
, принадлежащих промежутку I таких, что  выполняется соотношение:
выполняется соотношение:  .
. .
. называется точкой максимум а функции
называется точкой максимум а функции 


 , принадлежащего области определения функции,
, принадлежащего области определения функции,  также принадлежит области определения функции.
также принадлежит области определения функции. .
.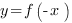 симметрична относительно начала координат.
симметрична относительно начала координат. .
. или
или  .
.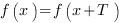



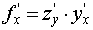 .
.

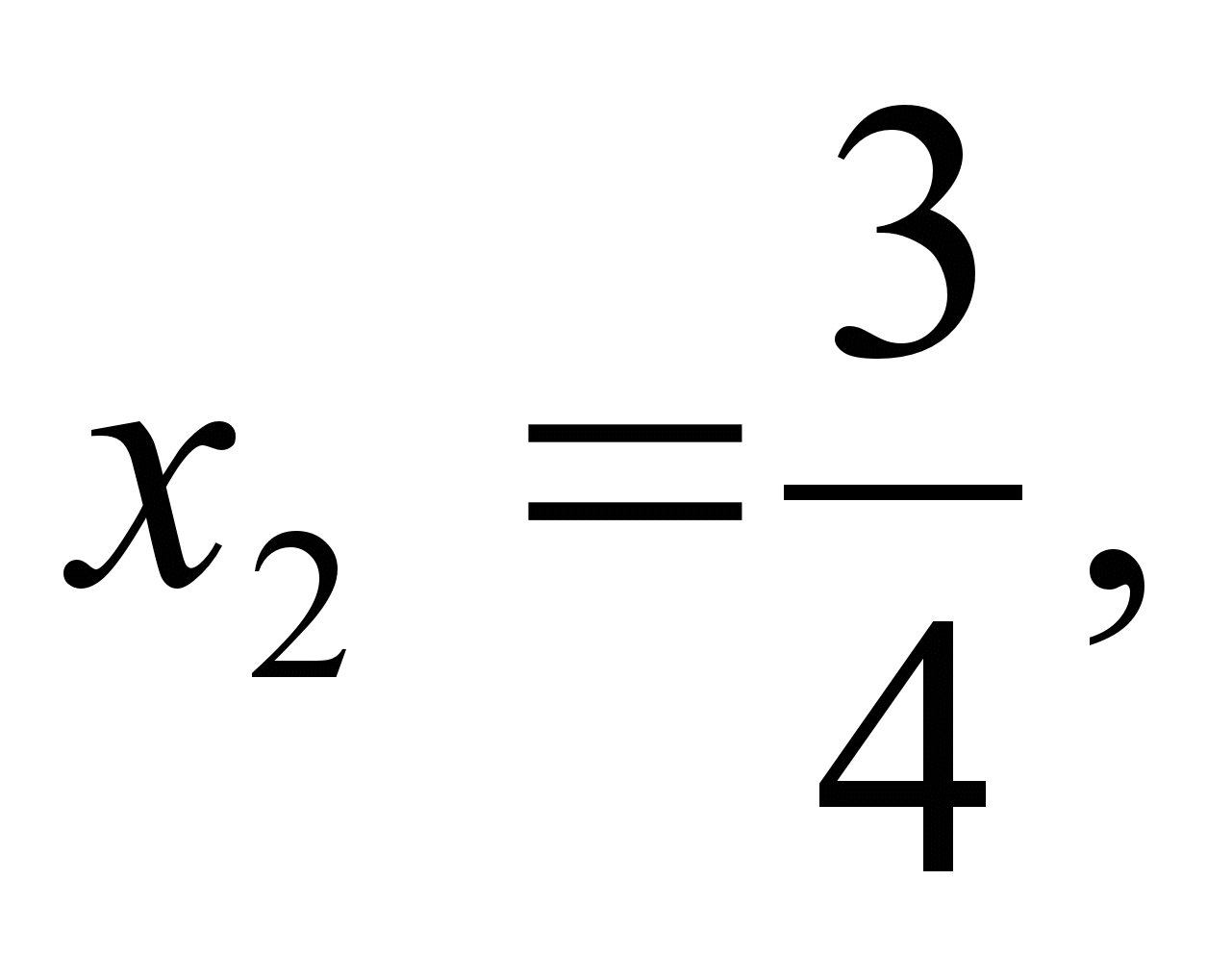
 ,...,
,...,  и т.д.
и т.д. , x1 =1.
, x1 =1. ,
, 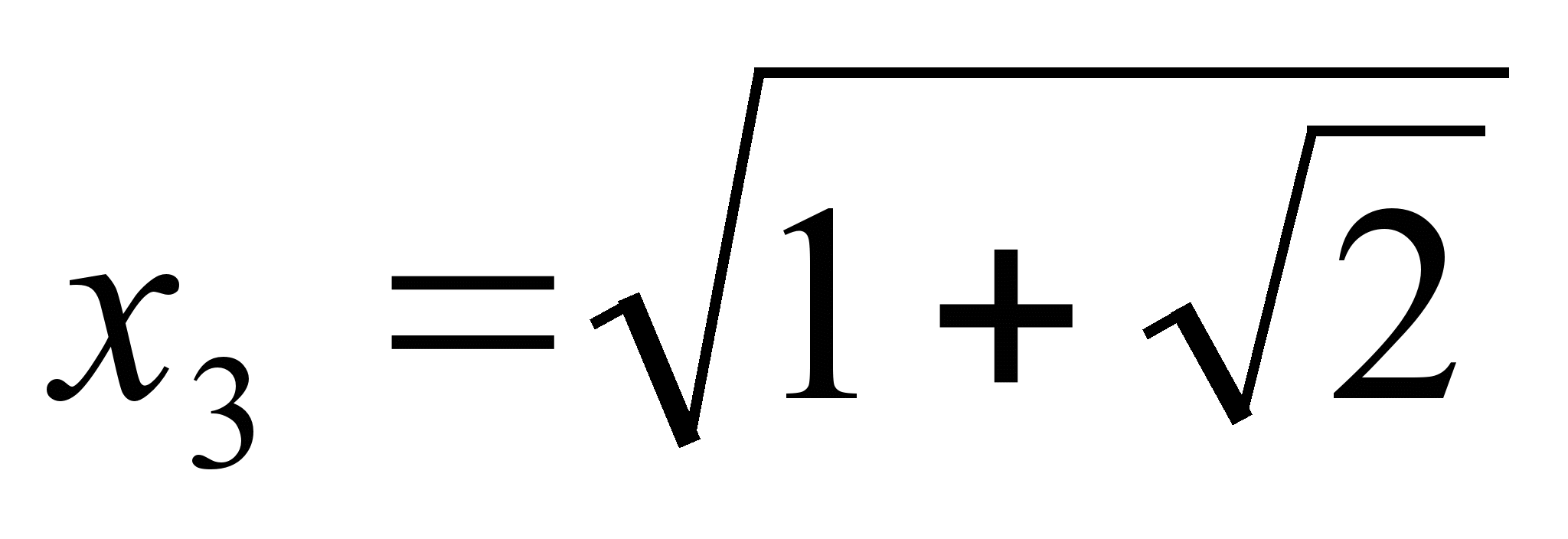 ,
, 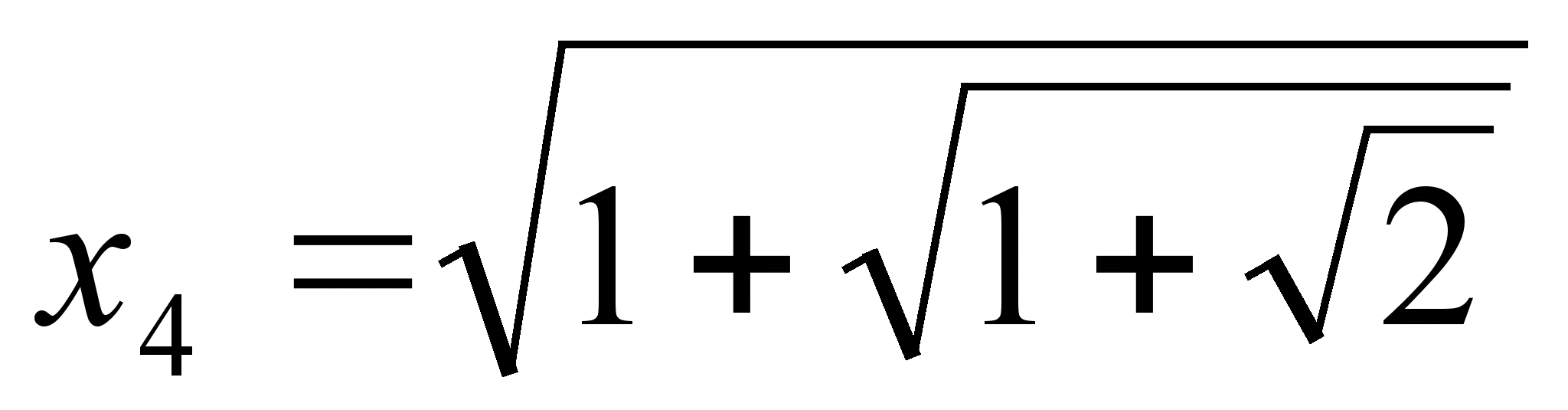 и т.д.
и т.д.


