

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Отыскание наибольшего и наименьшего значения функции. Критерий существования точек экстремума
Похожие статьи вашей тематики
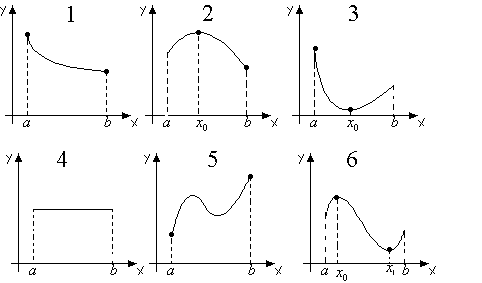 Дана функция Дана функция 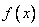 , определенная и непрерывная на некотором промежутке , определенная и непрерывная на некотором промежутке 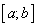 . Требуется найти наибольшее (наименьшее) значение функции на этом промежутке. . Требуется найти наибольшее (наименьшее) значение функции на этом промежутке.
Теоретические основы.
Теорема (Вторая теорема Вейерштрасса):
Если функция 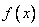 определена и непрерывна в замкнутом промежутке определена и непрерывна в замкнутом промежутке 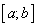 , то она достигает в этом промежутке своих наибольшего и наименьшего значений. , то она достигает в этом промежутке своих наибольшего и наименьшего значений.
Функция может достигать своих наибольших и наименьших значений либо на внутренних точках промежутка, либо на его границах. Проиллюстрируем все возможные варианты.
Пояснение:
1) Функция достигает своего наибольшего значения на левой границе промежутка в точке 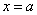 , а своего наименьшего значения на правой границе промежутка в точке , а своего наименьшего значения на правой границе промежутка в точке 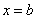 . .
2) Функция достигает своего наибольшего значения в точке 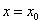 (это точка максимума), а своего наименьшего значения на правой границе промежутка в точке (это точка максимума), а своего наименьшего значения на правой границе промежутка в точке 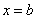 . .
3) Функция достигает своего наибольшего значения на левой границе промежутка в точке 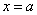 , а своего наименьшего значения в точке , а своего наименьшего значения в точке 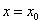 (это точка минимума). (это точка минимума).
4) Функция постоянна на промежутке, т.е. она достигает своего минимального и максимального значения в любой точке промежутка, причем минимальное и максимальное значения равны между собой.
5) Функция достигает своего наибольшего значения в точке 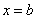 , а своего наименьшего значения точке , а своего наименьшего значения точке 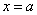 (несмотря на то, что функция имеет на этом промежутке как максимум, так и минимум). (несмотря на то, что функция имеет на этом промежутке как максимум, так и минимум).
6) Функция достигает своего наибольшего значения в точке 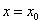 (это точка максимума), а своего наименьшего значения в точке (это точка максимума), а своего наименьшего значения в точке 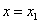 (это точка минимума). (это точка минимума).
Замечание:
«Максимум» и «максимальное значение» — разные вещи. Это следует из определения максимума и интуитивного понимания словосочетания «максимальное значение».
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция 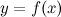 имеет экстремум в точке имеет экстремум в точке  , то ее производная , то ее производная 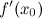 либо равна нулю, либо не существует. либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: 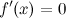 , называются стационарными точками функции. , называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения 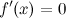 ), либо это точки, в которых производная ), либо это точки, в которых производная 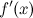 не существует. не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции 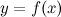 выполнены следующие условия: выполнены следующие условия:
1. функция непрерывна в окрестности точки  ; ;
2. 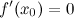 или или 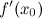 не существует; не существует;
3. производная 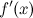 при переходе через точку при переходе через точку  меняет свой знак. меняет свой знак.
Тогда в точке  функция функция 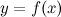 имеет экстремум, причем это минимум, если при переходе через точку имеет экстремум, причем это минимум, если при переходе через точку  производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку  производная меняет свой знак с плюса на минус. производная меняет свой знак с плюса на минус.
Если производная 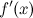 при переходе через точку при переходе через точку  не меняет знак, то экстремума в точке не меняет знак, то экстремума в точке  нет. нет.
Таким образом, для того чтобы исследовать функцию 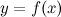 на экстремум, необходимо: на экстремум, необходимо:
1. найти производную 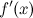 ; ;
2. найти критические точки, то есть такие значения  , в которых , в которых 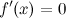 или или 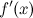 не существует; не существует;
3. исследовать знак производной слева и справа от каждой критической точки;
4. найти значение функции в экстремальных точках.
Выпуклость, вогнутость и точки перегиба
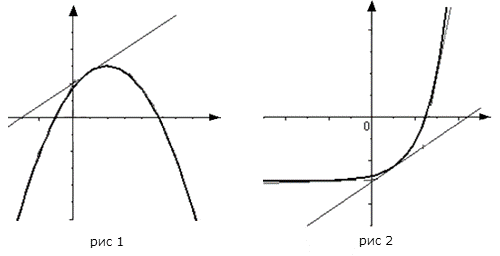
График функции 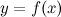 , дифференцируемой на интервале , дифференцируемой на интервале 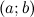 , является на этом интервале выпуклым, если график этой функции в пределах интервала , является на этом интервале выпуклым, если график этой функции в пределах интервала 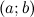 лежит не выше любой своей касательной (рис. 1). лежит не выше любой своей касательной (рис. 1).
График функции 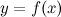 , дифференцируемой на интервале , дифференцируемой на интервале 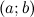 , является на этом интервале вогнутым, если график этой функции в пределах интервала , является на этом интервале вогнутым, если график этой функции в пределах интервала 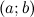 лежит не ниже любой своей касательной (рис. 2). лежит не ниже любой своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция 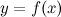 определена на интервале определена на интервале 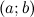 и имеет непрерывную, не равную нулю в точке и имеет непрерывную, не равную нулю в точке 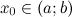 вторую производную. Тогда, если вторую производную. Тогда, если 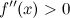 всюду на интервале всюду на интервале 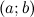 , то функция имеет вогнутость на этом интервале, если , то функция имеет вогнутость на этом интервале, если 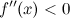 , то функция имеет выпуклость. , то функция имеет выпуклость.
Определение
Точкой перегиба графика функции 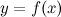 называется точка называется точка 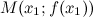 , разделяющая промежутки выпуклости и вогнутости. , разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция 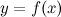 имеет перегиб в точке имеет перегиб в точке 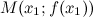 , то , то 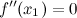 или не существует. или не существует.
Асимптоты графика функции
Асимптоты графика функции
Виды асимптот
Определение
Прямая  называется вертикальной асимптотой графика функции называется вертикальной асимптотой графика функции 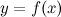 , если хотя бы одно из предельных значений , если хотя бы одно из предельных значений 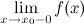 или или 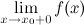 равно равно 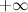 или или 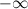 . .
Замечание. Прямая  не может быть вертикальной асимптотой, если функция непрерывна в точке не может быть вертикальной асимптотой, если функция непрерывна в точке  . Поэтому вертикальные асимптоты следует искать в точках разрыва функции. . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Определение
Прямая 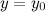 называется горизонтальной асимптотой графика функции называется горизонтальной асимптотой графика функции 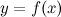 , если хотя бы одно из предельных значений , если хотя бы одно из предельных значений 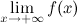 или или 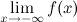 равно равно 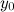 . .
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Определение
Прямая 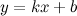 называется наклонной асимптотой графика функции называется наклонной асимптотой графика функции 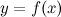 , если , если 
52. общий план исследования функции и построения графика
| |
Общий план исследования функции и построения графика.
1) Отыскивается область определения функции.
Исследование функции начинают с поиска области определения. Под областью определения понимается множество всех значений аргумента, при которых функция определена, то есть может быть вычислена. При нахождении области определения функции следует обращать внимание на выражения содержащие дроби, так как, знаменатель дроби не может обращаться в нуль. Следует обращать внимание на корни, так как, подкоренное выражение должно быть неотрицательным. Особое внимание следует обратить на логарифмы, входящие в выражение. Если функция содержит логарифм 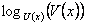 , то на область определения накладываются ограничения исходя из неравенств , то на область определения накладываются ограничения исходя из неравенств
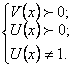 .
2) Исследуем общие свойства функции: чётность; нечётность; периодичность.Функция .
2) Исследуем общие свойства функции: чётность; нечётность; периодичность.Функция 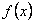 называется чётной, если называется чётной, если 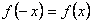 . График чётной функции симметричен относительно оси ординат. Например, функция . График чётной функции симметричен относительно оси ординат. Например, функция 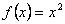 - чётная, так как - чётная, так как 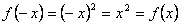 . Функция называется нечётной, если . Функция называется нечётной, если 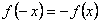 . График функции симметричен относительно начала координат (центральная симметрия). Для примера рассмотрим функцию . График функции симметричен относительно начала координат (центральная симметрия). Для примера рассмотрим функцию 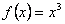 . Она нечётная, так как . Она нечётная, так как 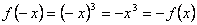 . Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения. Если существует . Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения. Если существует 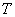 такое, что для любого такое, что для любого 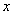 выполняется условие выполняется условие 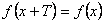 , то функция , то функция 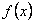 называется периодической. Наименьшее из чисел называется периодической. Наименьшее из чисел 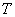 , удовлетворяющих указанному условию, называют периодом. График периодической функции строят так. Сначала строят график на одном периоде, а потом копируют построенный участок вдоль всей оси , удовлетворяющих указанному условию, называют периодом. График периодической функции строят так. Сначала строят график на одном периоде, а потом копируют построенный участок вдоль всей оси 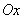 . Запись периодические функции, как правило, содержит тригонометрические функции синуса, косинуса, тангенса и котангенса.
3) Находим точки пересечения графика функции с осями координат.
Абсцисса пересечение с осью . Запись периодические функции, как правило, содержит тригонометрические функции синуса, косинуса, тангенса и котангенса.
3) Находим точки пересечения графика функции с осями координат.
Абсцисса пересечение с осью 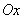 ищется исходя из уравнения ищется исходя из уравнения 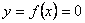 . Ордината пересечение с осью . Ордината пересечение с осью 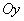 ищется подстановкой значения ищется подстановкой значения 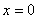 в выражение функции в выражение функции 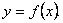 Если пересечение с осью Если пересечение с осью 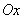 найти не удаётся, то обходятся без него. Обычно поиск пересечения с осью найти не удаётся, то обходятся без него. Обычно поиск пересечения с осью 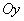 не представляет труда. 4) Исследуется непрерывность функции, находятся точки разрыва. Функция не представляет труда. 4) Исследуется непрерывность функции, находятся точки разрыва. Функция 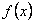 называется непрерывной в точке называется непрерывной в точке 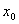 , если она определена в этой точке и существует предел , если она определена в этой точке и существует предел 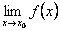 , который равен значению функции. То есть , который равен значению функции. То есть
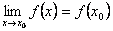 .
Функция называется непрерывной на промежутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка). График непрерывной функции может быть изображён без отрыва карандаша (мела, пера, ручки,…). Точка .
Функция называется непрерывной на промежутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка). График непрерывной функции может быть изображён без отрыва карандаша (мела, пера, ручки,…). Точка 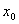 является точкой разрыва функции, если функция определена и непрерывна в окрестности точки является точкой разрыва функции, если функция определена и непрерывна в окрестности точки 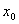 , а в самой точке не является непрерывной (хотя может быть определённой). В этом случае говорят, что функция терпит разрыв в точке , а в самой точке не является непрерывной (хотя может быть определённой). В этом случае говорят, что функция терпит разрыв в точке 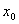 . Выделяют три типа точек разрыва: устранимый разрыв; конечный разрыв (разрыв первого рода); бесконечный разрыв (разрыв второго рода).
5) Ищутся асимптоты графика функции.
Прямая называется асимптотой графика функции, если расстояние от точек графика до этой прямой стремится к нулю при бесконечном удалении от начала координат вдоль графика функции. Образно выражаясь, график как бы прилипает к асимптоте. Асимптоты бывают вертикальные, наклонные и горизонтальные. Вертикальные асимптоты ищутся по точкам разрыва второго рода. Если в точке . Выделяют три типа точек разрыва: устранимый разрыв; конечный разрыв (разрыв первого рода); бесконечный разрыв (разрыв второго рода).
5) Ищутся асимптоты графика функции.
Прямая называется асимптотой графика функции, если расстояние от точек графика до этой прямой стремится к нулю при бесконечном удалении от начала координат вдоль графика функции. Образно выражаясь, график как бы прилипает к асимптоте. Асимптоты бывают вертикальные, наклонные и горизонтальные. Вертикальные асимптоты ищутся по точкам разрыва второго рода. Если в точке 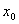 функция терпит бесконечный разрыв, то вертикальная прямая функция терпит бесконечный разрыв, то вертикальная прямая 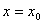 является вертикальной асимптотой. Например, в точке является вертикальной асимптотой. Например, в точке 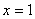 функция функция 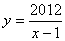 имеет разрыв второго рода. Следовательно, уравнение вертикальной асимптоты имеет разрыв второго рода. Следовательно, уравнение вертикальной асимптоты 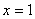 . График функции имеет наклонную асимптоту при . График функции имеет наклонную асимптоту при 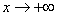 (соответственно при (соответственно при 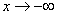 ), если существуют конечные пределы ), если существуют конечные пределы 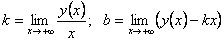 (соответственно (соответственно 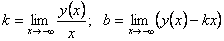 ). При этом уравнение наклонной асимптоты ). При этом уравнение наклонной асимптоты 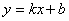 . Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет. Если . Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет. Если 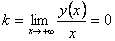 и существует конечный предел и существует конечный предел 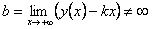 , то асимптота является горизонтальной и её уравнение , то асимптота является горизонтальной и её уравнение 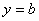 .
6) Находятся критические точки и интервалы монотонности.
Функция .
6) Находятся критические точки и интервалы монотонности.
Функция 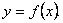 имеет максимум в точке имеет максимум в точке 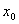 , если её значение в этой точке больше, чем её значения во всех точках некоторой окрестности, содержащей точку , если её значение в этой точке больше, чем её значения во всех точках некоторой окрестности, содержащей точку 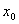 . Функция . Функция 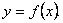 имеет минимум в точке имеет минимум в точке 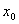 , если её значение в этой точке меньше, чем её значения во всех точках некоторой окрестности, содержащей точку , если её значение в этой точке меньше, чем её значения во всех точках некоторой окрестности, содержащей точку 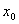 . Для определения критических точек находим производную по соответствующим правилам и используя таблицу производных. В критических точках производная равна нулю или не существует. Определяем знак производной в интервалах между критическими точками. Если на некотором интервале производная положительна, то функция возрастает. Если производная отрицательна, то на данном интервале функция убывает.
7) Ищутся точки перегиба и интервалы выпуклости.
Для определения точек перегиба находят вторую производную. В точке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая производная отрицательная, то график функции выпуклый вверх. 8)
На основании проведённого исследования строим график.
Если необходимо вычисляем значение функции в некоторых промежуточных точках. . Для определения критических точек находим производную по соответствующим правилам и используя таблицу производных. В критических точках производная равна нулю или не существует. Определяем знак производной в интервалах между критическими точками. Если на некотором интервале производная положительна, то функция возрастает. Если производная отрицательна, то на данном интервале функция убывает.
7) Ищутся точки перегиба и интервалы выпуклости.
Для определения точек перегиба находят вторую производную. В точке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая производная отрицательная, то график функции выпуклый вверх. 8)
На основании проведённого исследования строим график.
Если необходимо вычисляем значение функции в некоторых промежуточных точках.
|
Комплексные числа.(1 билет)
|



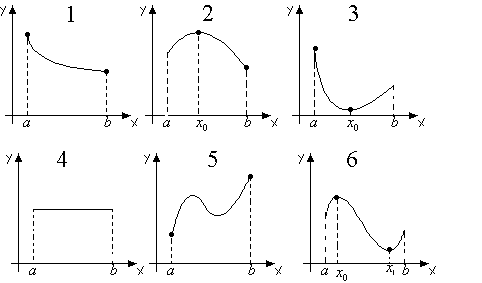 Дана функция
Дана функция 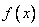 , определенная и непрерывная на некотором промежутке
, определенная и непрерывная на некотором промежутке 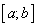 . Требуется найти наибольшее (наименьшее) значение функции на этом промежутке.
. Требуется найти наибольшее (наименьшее) значение функции на этом промежутке.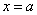 , а своего наименьшего значения на правой границе промежутка в точке
, а своего наименьшего значения на правой границе промежутка в точке 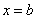 .
.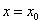 (это точка максимума), а своего наименьшего значения на правой границе промежутка в точке
(это точка максимума), а своего наименьшего значения на правой границе промежутка в точке 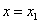 (это точка минимума).
(это точка минимума).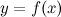 имеет экстремум в точке
имеет экстремум в точке  , то ее производная
, то ее производная 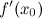 либо равна нулю, либо не существует.
либо равна нулю, либо не существует.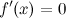 , называются стационарными точками функции.
, называются стационарными точками функции.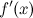 не существует.
не существует.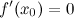 или
или  функция
функция  , в которых
, в которых 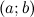 , является на этом интервале выпуклым, если график этой функции в пределах интервала
, является на этом интервале выпуклым, если график этой функции в пределах интервала 
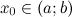 вторую производную. Тогда, если
вторую производную. Тогда, если 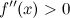 всюду на интервале
всюду на интервале 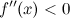 , то функция имеет выпуклость.
, то функция имеет выпуклость.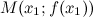 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.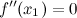 или не существует.
или не существует.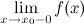 или
или 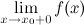 равно
равно 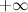 или
или 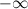 .
.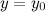 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 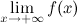 или
или 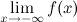 равно
равно 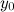 .
.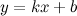 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 
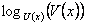 , то на область определения накладываются ограничения исходя из неравенств
, то на область определения накладываются ограничения исходя из неравенств
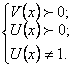 .
2) Исследуем общие свойства функции: чётность; нечётность; периодичность.Функция
.
2) Исследуем общие свойства функции: чётность; нечётность; периодичность.Функция 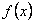 называется чётной, если
называется чётной, если 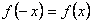 . График чётной функции симметричен относительно оси ординат. Например, функция
. График чётной функции симметричен относительно оси ординат. Например, функция 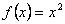 - чётная, так как
- чётная, так как 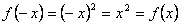 . Функция называется нечётной, если
. Функция называется нечётной, если 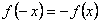 . График функции симметричен относительно начала координат (центральная симметрия). Для примера рассмотрим функцию
. График функции симметричен относительно начала координат (центральная симметрия). Для примера рассмотрим функцию 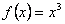 . Она нечётная, так как
. Она нечётная, так как 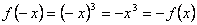 . Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения. Если существует
. Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения. Если существует 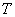 такое, что для любого
такое, что для любого 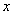 выполняется условие
выполняется условие 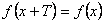 , то функция
, то функция 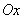 . Запись периодические функции, как правило, содержит тригонометрические функции синуса, косинуса, тангенса и котангенса.
3) Находим точки пересечения графика функции с осями координат.
Абсцисса пересечение с осью
. Запись периодические функции, как правило, содержит тригонометрические функции синуса, косинуса, тангенса и котангенса.
3) Находим точки пересечения графика функции с осями координат.
Абсцисса пересечение с осью 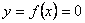 . Ордината пересечение с осью
. Ордината пересечение с осью 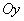 ищется подстановкой значения
ищется подстановкой значения 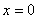 в выражение функции
в выражение функции 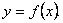 Если пересечение с осью
Если пересечение с осью 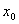 , если она определена в этой точке и существует предел
, если она определена в этой точке и существует предел 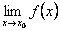 , который равен значению функции. То есть
, который равен значению функции. То есть
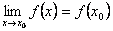 .
Функция называется непрерывной на промежутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка). График непрерывной функции может быть изображён без отрыва карандаша (мела, пера, ручки,…). Точка
.
Функция называется непрерывной на промежутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка). График непрерывной функции может быть изображён без отрыва карандаша (мела, пера, ручки,…). Точка 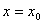 является вертикальной асимптотой. Например, в точке
является вертикальной асимптотой. Например, в точке 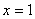 функция
функция 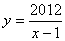 имеет разрыв второго рода. Следовательно, уравнение вертикальной асимптоты
имеет разрыв второго рода. Следовательно, уравнение вертикальной асимптоты 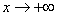 (соответственно при
(соответственно при 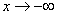 ), если существуют конечные пределы
), если существуют конечные пределы 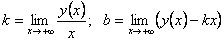 (соответственно
(соответственно 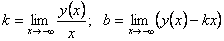 ). При этом уравнение наклонной асимптоты
). При этом уравнение наклонной асимптоты 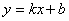 . Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет. Если
. Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет. Если 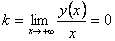 и существует конечный предел
и существует конечный предел 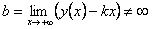 , то асимптота является горизонтальной и её уравнение
, то асимптота является горизонтальной и её уравнение 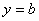 .
6) Находятся критические точки и интервалы монотонности.
Функция
.
6) Находятся критические точки и интервалы монотонности.
Функция 


