Зависимость между корнями алгебраического уравнения и его коэффициентами

Виета теорема — установленная Ф. Виетом теорема: сумма корней приведенного квадратного уравнения равна коэффициенту при x, взятому с противоположным знаком, а произведение — свободному члену

Известны «формулы Виета», дающие зависимость между корнями и коэффициентами алгебраического уравнения

Свойства корней квадратного уравнения.

Дискриминант. Теорема Виета.

 

Формула корней неприведенного квадратного уравнения:

показывает, что возможны три случая:   1) b ^2– 4 a c > 0, тогда имеются два различных корня;   2) b ^2– 4 a c = 0, тогда имеются два равных корня;   3) b ^2– 4 a c < 0, тогда имеются два комплексных корня.   Выражение b ^2– 4 a c,от значения которого зависит, какой случай имеет место, называется дискриминантомквадратного уравнения и обозначается через D. Теорема Виета.Сумма корней приведенного квадратного уравненияx ^2 + px+ q = 0 равна коэффициенту при первой степени неизвестного, взятому с обратным знаком: x 1 + x 2 = – p, а произведение равно свободному члену: x 1· x 2 = q. Для доказательства теоремы Виета достаточно воспользоваться формулой корней приведенного квадратного уравнения.

Рациональные алгебраические дроби. Простейшие рац. дроби

Разложение правильной рац. Дроби на простейшие

 

· билет) неопределенный интеграл

Неопределенный интеграл и его свойства. Простейшие правила интегрирования. Таблица основных интегралов

Геометрическое и механическое истолкование задачи нахождения первообразной ф-ции

геом смысл.

Теорема 2. Если F ₁ (x) и F ₂ (x) - две первообразные для функции f(x), то они отличаются на постоянное слагаемое.

Доказательство. Рассмотрим функцию

Ф(х) = F ₁ (x) - F ₂ (x).

Ф'(х) = F ₁ '(x) - F ₂ '(x) = f(x) - f(x) = 0,

Ф(х) = C,

F ₁ (x) = F ₂ (x) +C.

 

Первообразные имеют следующий геометрический смысл.

Пусть F ₁ (x) и F ₂ (x) - первообразные функции y=f(x). Найдем их производные в точке х ₀.

F ₁ '(х ₀ ) = f(х ₀ ), касательные к графикам функций y = F ₁ (x) и y = F ₂ (x)
F ₂ '(х ₀ ) = f(х ₀ ), в любой точке параллельны.

Следовательно, и сами графики будут располагаться параллельно.

На основании теоремы 2 F ₁ (x) и F ₂ (x) отличаются на постоянное слагаемое, следовательно, один график можно получить из другого сдвигом на C единиц вдоль оси ОY.

F ₁(x) = F ₂(x) + C.

 

Функция имеет бесконечно много первообразных, которые отличаются друг от друга на постоянное слагаемое. Графики всех первообразных представляют собой бесконечное семейство параллельных кривых, которые заполняют всю плоскость. Через каждую точку плоскости проходит график одной из первообразных.

Мех.смысл

Если функция f (х) непрерывна на отрезке [ a; b ], то она интегрируема на этом отрезке..
1) Путь s, пройденный точкой по прямой за время co скоростью v = v (t) (v (t)непрерывна на ), есть

(механический смысл определенного интеграла).

Интегрирование заменой переменной

Интегрирование по частям

Интегрирование рац. дробей

Метод Остроградского

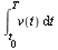
Остроградского метод интегрирования рациональных дробей. Рассмотрим рациональную дробь – выражение вида , где числитель и знаменатель – многочлены степени m и n соответственно. При этом мы будем рассматривать случай, когда дробь правильная, т.е. когда 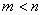, в противном случае сначала выделим «целую часть» дроби (см. Дробь рациональная, Дробь смешанная).
В случае, когда знаменатель рациональной дроби имеет несколько корней большой кратности и не имеет простых корней (т.е. корней кратности 1 – см. Корень многочлена), при ее интегрировании удобно применять метод Остроградского.
Суть метода состоит в том, что интеграл представляют в следующем виде:
, (1)
где знаменатель подынтегральной функции правой части – многочлен – имеет лишь простые корни, причем они – все различные корни многочлена Q_n (x); знаменатель первого слагаемого правой части – многочлен 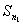– частное от деления многочлена Q_n (x) на многочлен , а числители обоих слагаемых правой части – многочлены и – многочлены с неопределенными коэффициентами, степени которых на 1 меньше степеней соответствующих знаменателей.
После нахождения всех четырех многочленов правой части (это делается с помощью почленного дифференцирования выписанного выше равенства Остроградского (1)) полученный справа интеграл легко считается методом разложения на простейшие дроби, причем из-за того, что все корни знаменателя подынтегральной функции правой части простые, получаются табличные интегралы вида и/или , где p ² – 4 q < 0 – знаменатель дроби в подынтегральной функции последнего интеграла не имеет действительных корней.