
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование выражений, содержащих тригонометрические ф-цииСодержание книги
Поиск на нашем сайте
Интегралы вида Интегралы указанного вида сводятся к интегралам от рациональной функции новой переменной t с помощью подстановки Замечание. Универсальная тригонометрическая подстановка часто приводит к громоздким вычислениям. Поэтому чаще применяются другие подстановки. 2. Подынтегральная функция
или условию
Тогда можно использовать подстановку
3. Подынтегральная функция 4. Вычисление интегралов вида В этом случае полезно пользоваться следующими правилами: А) если m - нечетное положительное число, то вносим
В) если число m+n является четным отрицательным числом, то можно сделать замену переменной
Примечание. В общем случае интегралы вида
5. При вычислении интегралов вида 6. Интегралы вида Для вычисления интегралов указанного вида применяют тригонометрические формулы:
Тригонометрические подстановки В данной секции мы рассмотрим вычисление интегралов вида Предварительно преобразуем квадратичную функцию под знаком корня, выделив в ней полный квадрат:
Выполнив замену
Каждый из этих трех интегралов вычисляется с помощью специальных тригонометрических или гиперболических подстановок.
1. Интегралы вида Тригонометрическая подстановка:
2. Интегралы вида Тригонометрическая подстановка:
Гиперболическая подстановка:
3. Интегралы вида Тригонометрическая подстановка:
Неберущиеся интегралы
Определенный интеграл 1.Определенные интегралы (интеграл Римана). Пусть действительная функция f (x) определена и ограничена на ограниченном замкнутом интервале [ a, b ]. Разобъем этот интервал на n частичных интервалов точками a = x 0< x 1< x 2<... < xn = b. Выберем в каждом из частичных интервалов по произвольной точке Если существует предел интегральной суммы при стремлении к нулю длины наибольшего частичного интервала разбиения:
называется определенным интегралом от f (x) по интервалу [ a, b ] в смысле Римана (интеграл Римана). Это определение означает, что для любого положительного числа
и при любом выборе промежуточных точек
Функция f (x) называется подынтегральной функцией, а a и b - пределами интегрирования.
2. Суммы Дарбу и их свойства.
Пусть функция
Назовём С в о й с т в о 1. Для любой выборки
○ Так как для любого
то
Складывая эти неравенства, получаем
Согласно определению сумм Дарбу и интегральной суммы С в о й с т в о 2. Спараведливы равенства
С в о й с т в о 3. Если разбиение
т.е. при измельчении разбиения нижняя сумма Дарбу не уменьшается, а верхняя не увеличивается. С в о й с т в о 4. Для любых разбиений
С в о й с т в о 5. Существуют числа
Удовлетворяющие для любых разбиений
Эти числа называют соответственно нижним и верхним интегралами Дарбу от функции
3. Условия существования определенного интеграла Определение. Функция Теорема 1. Если функция Сформулируем и более общую теорему об интегрируемости. Теорема 2. Если функция
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.68 (0.01 с.) |

 , где
, где  рациональная функция от u и v.
рациональная функция от u и v.
 , которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии
, которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии 
 удовлетворяет условию
удовлетворяет условию (1)
(1) . (2)
. (2) ,
, 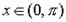 или
или 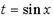 ,
,  соответственно. Смотри пример 2.
соответственно. Смотри пример 2. . Это условие выполняется в частности для функций, содержащих только четные степени
. Это условие выполняется в частности для функций, содержащих только четные степени 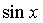 и
и  В этом случае часто применяют замену переменной
В этом случае часто применяют замену переменной  , где
, где  , где
, где  .При этом, так как
.При этом, так как  или
или 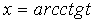 ,то
,то  . Функции
. Функции  и
и  . Смотри пример 3.
. Смотри пример 3. , где m и n? целые числа.
, где m и n? целые числа. . Сравни с 1. Смотри пример 4.
. Сравни с 1. Смотри пример 4. ,
,  и
и  . Смотри пример 5.
. Смотри пример 5. , где m и n - целые числа, вычисляются с помощью рекуррентных формул, которые выводятся путем интегрирования по частям.
, где m и n - целые числа, вычисляются с помощью рекуррентных формул, которые выводятся путем интегрирования по частям. или
или 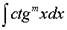 где m - натуральное число,
где m - натуральное число,  используют тригонометрические формулы
используют тригонометрические формулы  или, соответственно,
или, соответственно,  . Смотри пример 8.
. Смотри пример 8.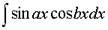 ,
,  ,
,  .
.


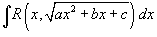 , где R - рациональная функция x и квадратного корня
, где R - рациональная функция x и квадратного корня  .
.
 , мы получим один из следующих 3 интегралов в зависимости от значений коэффициентов a, b и с:
, мы получим один из следующих 3 интегралов в зависимости от значений коэффициентов a, b и с:


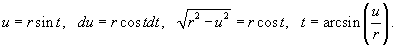

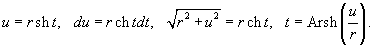


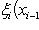

 и составим сумму (интегральная сумма)
и составим сумму (интегральная сумма) 

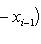 .
.
 , то функция f (x) называется интегрируемой в смысле Римана на интервале [ a, b ]. Предел этой суммы
, то функция f (x) называется интегрируемой в смысле Римана на интервале [ a, b ]. Предел этой суммы

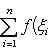




 существует такое число
существует такое число  , что при любом разбиении интервала [ a, b ] на частичные интервалы, длины которых меньше
, что при любом разбиении интервала [ a, b ] на частичные интервалы, длины которых меньше  .
.


 выполняется неравенство
выполняется неравенство




 , определённая на отрезке
, определённая на отрезке  , ограничена на этом отрезке и пусть
, ограничена на этом отрезке и пусть  - разбиение отрезка
- разбиение отрезка  (i=1,n). Обозначим
(i=1,n). Обозначим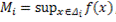 ,
,  ,
, ,
,  . (5)
. (5) и
и  соответственно верхней и нижней суммами Дарбу для функции
соответственно верхней и нижней суммами Дарбу для функции 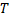 отрезка
отрезка  . Рассмотрим свойства сумм Дарбу.
. Рассмотрим свойства сумм Дарбу. . (6)
. (6) , выполняются неравенства
, выполняются неравенства


 . (7)
. (7) утверждения (7) и (6) равносильны. ●
утверждения (7) и (6) равносильны. ● , (8)
, (8)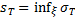 . (9)
. (9) - продолжение разбиения
- продолжение разбиения  , то
, то (10)
(10) и
и  справедливо неравенство
справедливо неравенство
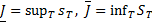 ,
, отрезка
отрезка  (12)
(12) , для которой на отрезке [ a; b ] существует определенный интеграл, называется интегрируемой на этом отрезке.
, для которой на отрезке [ a; b ] существует определенный интеграл, называется интегрируемой на этом отрезке.


