Определение ограниченной и неограниченной функции. Теорема об ограниченной функции, имеющей предел. . Теорема об ограниченности обратной функции.
Похожие статьи вашей тематики
Пусть задана функция y=f(x), определенная на некотором множестве D значений аргумента.
Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D.
Пример:
Функция y=sin x, определенная при -∞<x<+∞,>0, что при всех значениях х, удовлетворяющих неравенству |x|>N, функция f(x) ограничена.
Если функция f(x) имеет предел в точке a 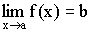 ,то она ограничена в некоторой окрестности точки a. ,то она ограничена в некоторой окрестности точки a.
Доказательство:
Пусть 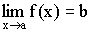 , тогда , тогда  , отсюда , отсюда
получаем  . Обратное неверно. . Обратное неверно.
Контрольный пример:
 в окрестности точки 0. в окрестности точки 0.
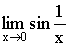 – не существует. – не существует.
Бесконечно малые и их свойства.
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если  или или  , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
 Примеры. Примеры.
- Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как
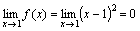 (см. рис.). (см. рис.). - Функция f(x) = tgx – бесконечно малая при x→0.
- f(x) = ln (1+x)– бесконечно малая при x→0.
- f(x) = 1/x– бесконечно малая при x→∞.
Основные свойства бесконечно малых функций (б.м.) 1° Сумма конечного числа б.м. функций является функцией бесконечно малой.
2° Произведение б функции на ограниченную есть функция бесконечно малая.
3° Произведение двух б.м функций есть функция бесконечно малая..
4° Произведение б.м функции на константу является бесконечно малой функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция бесконечно малая.
6° Функция  , обратная к б.м функции , обратная к б.м функции 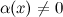 , есть функция бесконечно большая. Верно и обратное. , есть функция бесконечно большая. Верно и обратное.
Основные теоремы о пределах.
Теорема 1. Предел суммы равен сумме пределов, если они
существуют: 
Доказательство:

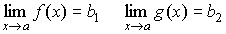
Из теоремы о связи между пределом и бесконечно малой величиной следует:


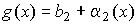
Получаем  
Теорема 2. Предел произведения равен произведению пределов, если они существуют: 
Доказательство:


Из теоремы о связи между пределом и бесконечно малой величиной следует: 

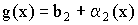
Получаем  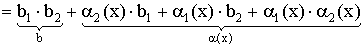  Теорема 3. Предел частного равен частному пределов: Теорема 3. Предел частного равен частному пределов:  . При . При
условии: все пределы существуют и 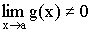 . .
Доказательство:


Из теоремы о связи между пределом и бесконечно малой величиной следует:
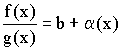
 ; ;
Получаем: 
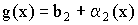

Теорема 4. Предел сохраняет знак неравенства. Если 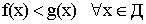  . .
Доказательство:
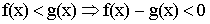
Следовательно,  
Следствие:

Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел: 
20-21. Первый и второй замечательные пределы и следствия.
Теорема. Первый замечательный предел  . .
Доказательство (геометрическое):

 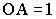
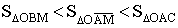
 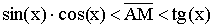
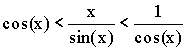

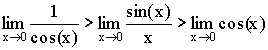
Так как  , то , то  . .
Следствия из теоремы:
1) 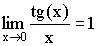
2) 
3) 
4) 
5) 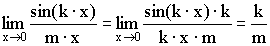
Теорема. Второй замечательный предел  . .
Доказательство:
Бином Ньютона:
 , где , где 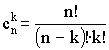 . .
Используем бином Ньютона для доказательства неравенства: 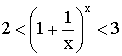

Отсюда заключаем, что 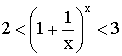 , а значит , а значит 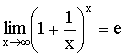 . .
Следствия из теоремы:
1) 
2) 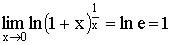
3) 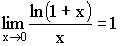
4) 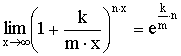
22. Сравнения бесконечно малыхвеличин (б.м.в.) Эквивалентные бесконечно малые.
Пусть 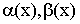 – бесконечно малые величины при – бесконечно малые величины при  , т.е. , т.е.  . .
Определение 1. Если  , то , то 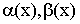 – б.м.в. одного порядка малости. – б.м.в. одного порядка малости.
Определение 2. Если 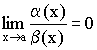 , то , то 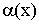 – б.м.в. более высокого порядка, чем – б.м.в. более высокого порядка, чем  . .
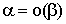 – –  более высокого порядка, чем более высокого порядка, чем  ("о" – читается как "о малое"). ("о" – читается как "о малое").
 – –  более низкого порядка, чем более низкого порядка, чем  ("О" – читается как "О большое"). ("О" – читается как "О большое").
Определение 3. Если  , то , то 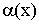 и и  эквивалентны – эквивалентны – 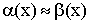 . .
Следствие из определения 3:  при при 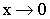 Теорема. Если Теорема. Если  и и  эквивалентны ( эквивалентны ( ), то ), то 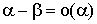 и и  Доказательство: Доказательство:
Пусть 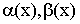 – бесконечно малые величины при – бесконечно малые величины при  и они эквивалентны и они эквивалентны  ). ).
Тогда  . .
Б.м. функции 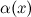 и и 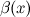 называются эквивалентными или равносильными б.м. одного порядка при называются эквивалентными или равносильными б.м. одного порядка при 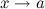 , если , если 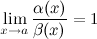
Обозначают: 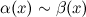 при при 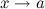 . .
Непрерывность функции. Определение непрерывности функции в точке и на промежутке. Теорема об арифметических действиях над непрерывными функциями. Непрерывность сложной функции. Ограниченность непрерывной функции.
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области .
Функция  называется непрерывной справа в точке называется непрерывной справа в точке  , если , если  . .
Функция  называется непрерывной слева в точке называется непрерывной слева в точке  , если , если  . .
Функция 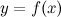 называется непрерывной в интервале называется непрерывной в интервале  , если она непрерывна в каждой точке этого интервала. , если она непрерывна в каждой точке этого интервала.
Функция 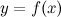 называется непрерывной на отрезке называется непрерывной на отрезке  , если она является непрерывной в интервале , если она является непрерывной в интервале 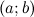 , непрерывной справа в точке , непрерывной справа в точке  , то есть , то есть  и непрерывной слева в точке и непрерывной слева в точке  , то есть , то есть  . .
Теорема об арифметических действиях:
Если функция f(x)- непрерывна в т. x0, j(x) непрерывна в т. x0, тогда:
1) f(x) ± j(x) - непрерывная функция в т. x0,
2) f×j - непрерывная функция в т. x0,
3) f/j, j(x0)¹0 - непрерывно в т. x0.
26. Теорема Вейерштрасса об ограниченности функции на замкнутом промежутке.
1) Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.
И 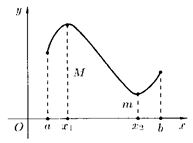 зображенная на рисунке зображенная на рисунке
функция  непрерывна на отрезке непрерывна на отрезке 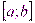 и принимает свое наибольшее значение M в точке и принимает свое наибольшее значение M в точке 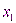 , а наименьшее m – вточке , а наименьшее m – вточке  . Для любого . Для любого  справедливо неравенство: справедливо неравенство:  . .
2) Если функция  непрерывна на отрезке непрерывна на отрезке  , то она ограничена на этом отрезке, т.е. существует постоянная , то она ограничена на этом отрезке, т.е. существует постоянная 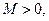 такая, что такая, что 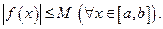
27. Теорема Больцано-Коши о промежуточном значении функции.
Если непрерывная функция, определённая на вещественном интервале, принимает два значения, то она принимает и любое значение между ними.
Следствия теоремы Больцано-Коши
1. Теорема о нуле непрерывной функции.
Если функция непрерывна на некотором отрезке и на концах этого отрезка принимает значения противоположных знаков, то существует точка, в которой значение функции равно нулю.
2. В частности любой многочлен нечётной степени имеет, по меньшей мере, один нуль.
28. Определение обратной функции. Теорема о непрерывности обратной функции.
Определение: Пусть функция y=f(x) с областью определения D(f) и множеством значений R(f). Обратная к f — функция f−1 определяется как функция с областью определения D(f−1)=R(f) и множеством значений R(f−1)=D(f), такая что f−1(y)=x тогда и только тогда, когда f(x)=y. Таким образом, f−1 возвращает y обратно в x.
Примеры:
Найти функцию, обратную функции y=3x+5.
Решение: Функция y=3x+5 определена и возрастает на всей числовой оси. Следовательно, обратная функция существует и возрастает. Разрешая уравнение относительно x, получим x=(y−5)/3.
Показать, что функция y=kx, где (k≠0) обратна сама себе.
Решение: Функция y=kx определена и монотонна на всей числовой оси, кроме точки x=0. Следовательно, обратная функция существует. Область значений функции — вся числовая ось, кроме точки y=0. Разрешая уравнение относительно x, получим x=k/y.
Теорема о непрерывности обратной функции:
Если 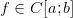 и и  строго возрастает(убывает) на строго возрастает(убывает) на  , то на , то на  определена функция определена функция  , которая будет обратная к , которая будет обратная к  , непрерывная на , непрерывная на  и строго возрастать(убывать) на и строго возрастать(убывать) на  . .
Доказательство:
Предположим, что функция  строго возрастает на промежутке строго возрастает на промежутке  . .
По следствию из функций область значений  непрерывной функции непрерывной функции  тоже есть промежуток. тоже есть промежуток.
В силу строгого возрастания функции  для каждого для каждого 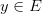 существует единственная точка существует единственная точка 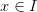 такая, что такая, что 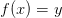 . .
Следовательно, для функции  существует обратная функция существует обратная функция 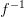 определенная на промежутке определенная на промежутке  и с множеством значений и с множеством значений 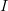 . .
Покажем, что 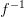 строго возрастает на строго возрастает на  . .
Пусть 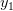 и и  — две произвольные точки из — две произвольные точки из  , такие, что , такие, что  и прообразами этих точек будут точки и прообразами этих точек будут точки 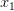 и и  . . 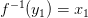 и и  . .
Поскольку  — строго возрастающая функция, то неравенство — строго возрастающая функция, то неравенство  возможно тогда и только тогда когда возможно тогда и только тогда когда 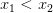 или тоже самое, когда или тоже самое, когда  . .
В силу произвольности 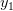 делаем вывод, что функция делаем вывод, что функция 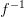 — строго возрастает на множестве — строго возрастает на множестве  . .
|



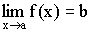 ,то она ограничена в некоторой окрестности точки a.
,то она ограничена в некоторой окрестности точки a. , отсюда
, отсюда . Обратное неверно.
. Обратное неверно. в окрестности точки 0.
в окрестности точки 0.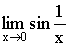 – не существует.
– не существует. или
или  , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. Примеры.
Примеры.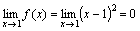 (см. рис.).
(см. рис.). , обратная к б.м функции
, обратная к б.м функции 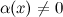 , есть функция бесконечно большая. Верно и обратное.
, есть функция бесконечно большая. Верно и обратное.

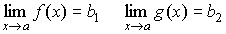


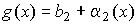






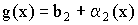

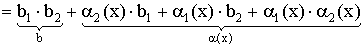
 Теорема 3. Предел частного равен частному пределов:
Теорема 3. Предел частного равен частному пределов:  . При
. При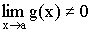 .
.

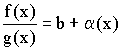


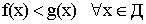
 .
.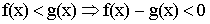




 .
. 

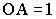
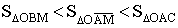

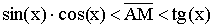
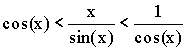

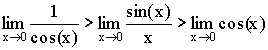
 , то
, то 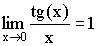



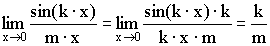
 .
.  , где
, где  .
.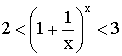

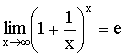 .
.
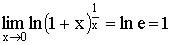
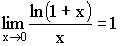
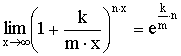
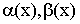 – бесконечно малые величины при
– бесконечно малые величины при  , т.е.
, т.е.  .
. , то
, то 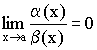 , то
, то 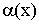 – б.м.в. более высокого порядка, чем
– б.м.в. более высокого порядка, чем  .
.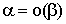 –
–  более высокого порядка, чем
более высокого порядка, чем  ("о" – читается как "о малое").
("о" – читается как "о малое"). –
–  , то
, то 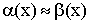 .
. при
при 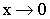 Теорема. Если
Теорема. Если  ), то
), то 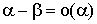 и
и  Доказательство:
Доказательство: .
.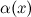 и
и 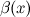 называются эквивалентными или равносильными б.м. одного порядка при
называются эквивалентными или равносильными б.м. одного порядка при 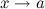 , если
, если 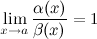
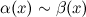 при
при 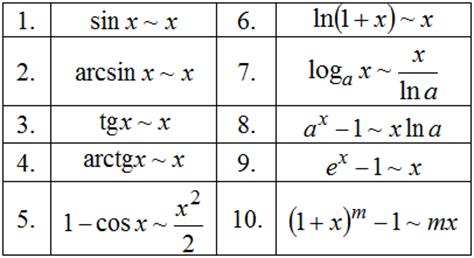
 называется непрерывной справа в точке
называется непрерывной справа в точке  , если
, если 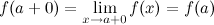 .
.  .
.  называется непрерывной в интервале
называется непрерывной в интервале 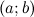 , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала. , если она является непрерывной в интервале
, если она является непрерывной в интервале  и непрерывной слева в точке
и непрерывной слева в точке  , то есть
, то есть  .
. зображенная на рисунке
зображенная на рисунке непрерывна на отрезке
непрерывна на отрезке 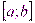 и принимает свое наибольшее значение M в точке
и принимает свое наибольшее значение M в точке 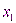 , а наименьшее m – вточке
, а наименьшее m – вточке  . Для любого
. Для любого  справедливо неравенство:
справедливо неравенство:  .
. непрерывна на отрезке
непрерывна на отрезке  , то она ограничена на этом отрезке, т.е. существует постоянная
, то она ограничена на этом отрезке, т.е. существует постоянная 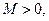 такая, что
такая, что 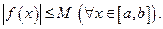
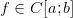 и
и  строго возрастает(убывает) на
строго возрастает(убывает) на  , то на
, то на  определена функция
определена функция  , которая будет обратная к
, которая будет обратная к  .
. непрерывной функции
непрерывной функции 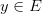 существует единственная точка
существует единственная точка 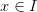 такая, что
такая, что 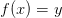 .
.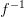 определенная на промежутке
определенная на промежутке  и с множеством значений
и с множеством значений 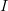 .
.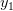 и
и  — две произвольные точки из
— две произвольные точки из  и прообразами этих точек будут точки
и прообразами этих точек будут точки 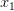 и
и  .
. 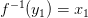 и
и  .
. возможно тогда и только тогда когда
возможно тогда и только тогда когда 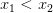 или тоже самое, когда
или тоже самое, когда  .
.


