
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная матрица. Теоремы о существовании и единственности обратной матрицы.Содержание книги
Поиск на нашем сайте
Обратная матрица. Теоремы о существовании и единственности обратной матрицы. Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
Теорема ( Теорема единственности +6. Минор k–го порядка. Ранг матрицы. Трапецевидная матрица. Теорема о ранге матрицы трапецевидной формы Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.
Если у матрицы A среди ее миноров есть хотя бы один ненулевой минор порядка r, а все миноры больших порядков равны нулю, то число r называется рангом матрицы A Обозначается r = r(A)
Теорема. Ранг трапециевидной матрицы равен числу ее ненулевых строк.
7. Элементарные преобразования матриц. Эквивалентные матрицы. Теоремы о ранге эквивалентных матриц и о приведении матрицы к трапецевидной форме. Элементарные преобразования: 1) Перестановка строк(столбцов) 2) Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и тоже число. Теорема: Элементарные преобразования не изменяют ранг матрицы, если A Теоремa: Любую матрицу используя элементарные преобразования строк, перестановку столбцов, можно привести к трапециевидной форме.
9. Сформулировать критерий совместности системы и теорему о числе решений. Метод Гаусса. Теорема критерий совместности системы Система совместна, когда ранг основной матрицы системы равен рангу расширенной матрицы r(A)=r(A/B) Теорема (О числе решений) Пусть система совместна (r(A)=r(A/B)=r).Если r=n (n-число неизвестных),то система определенна,если ранг r<n,то система не определенна. Замечание: если система неопределенная,то неизвестные соответствующие первые rстолбца трапецевидной матрицы называются базисами, а остальные n=r называются свободными. Метод Гауса: Пусть дана система из уравнений с nнеизвестной. Матрица вида: (А/В)= 1)Выписываем расширенную матрицей систему и с помощью элементарных преобразований строк и перестановки столбцов за исключением последнего столбца приводим ее к трапецевидной форме 2)Анализируем полученную матрицу
10. Крамеровская система уравнений. Метод Крамера. Матричный метод. Крамеровская система уравнений Пусть основная матрица системы квадратная (число уравнений равно числу неизвестных и определитель матрицы Метод Крамера: Решение Крамеровcкой системы A*X=Bможно найти по формулам Крамера: Xi=
Для системы из 3-х уравнений имеет:
X1= X2= ,X3=
11. Однородные системы уравнений. Теоремы о существовании ненулевого решения однородной системы. Однородные системы уравнений. Частный случай. а11x1+a12x2+..+a1nxn=0 а21x1+a22x2+..+a2nxn=0 а31x1+a32x2+..+a3nxn=0 ...... аm1xm+am2xm+..+amnxm=0 Такая система называется однородной, т.к. расширенная матрица отличается от основной матрицы лишь наличием нулевого столбца, который не может повлиять на ранг матрицы. Однородная система ВСЕГДА СОВМЕСТНА. Однородная система всегда имеет нулевое уравнение: x1=x2=xn=0
Теорема: Однородная система имеет ненулевые решения тогда и только тогда, когда ранг основной матрицы системы меньше числа неизвестных. Однородные системы решаются методом Гауса.
Линейные операции над векторами в координатной форме. Условие коллинеарности векторов (в координатах). а = (x1,y1,z2), b =(x2,y2,z2) Сложение (вычитание) а 2)Умножение вектора на число
Условия коллинеарности 2-х векторов: а||в Векторы а||в, тогда и только тогда, когда их координаты пропорциональны.
Общее уравнение плоскости. Взаимное расположение плоскостей Общее уравнение плоскости: A x + B y + C z + D = 0
Обратная матрица. Теоремы о существовании и единственности обратной матрицы. Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
Теорема ( Теорема единственности +6. Минор k–го порядка. Ранг матрицы. Трапецевидная матрица. Теорема о ранге матрицы трапецевидной формы Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.
Если у матрицы A среди ее миноров есть хотя бы один ненулевой минор порядка r, а все миноры больших порядков равны нулю, то число r называется рангом матрицы A Обозначается r = r(A)
Теорема. Ранг трапециевидной матрицы равен числу ее ненулевых строк.
7. Элементарные преобразования матриц. Эквивалентные матрицы. Теоремы о ранге эквивалентных матриц и о приведении матрицы к трапецевидной форме. Элементарные преобразования: 1) Перестановка строк(столбцов) 2) Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и тоже число. Теорема: Элементарные преобразования не изменяют ранг матрицы, если A Теоремa: Любую матрицу используя элементарные преобразования строк, перестановку столбцов, можно привести к трапециевидной форме.
9. Сформулировать критерий совместности системы и теорему о числе решений. Метод Гаусса.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

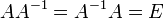
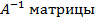 ) для того чтобы существовала
) для того чтобы существовала  к матрице А(необходимо, чтобы определитель матрицы был
к матрице А(необходимо, чтобы определитель матрицы был 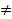 0).
0). Если
Если  B, то r(A)=r(B).
B, то r(A)=r(B). )-называется расширенной матрицей системы шаги Метода Гауса
)-называется расширенной матрицей системы шаги Метода Гауса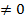 ,такая система называется Крамеровской.
,такая система называется Крамеровской.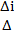 , i=1,2,...n |,
, i=1,2,...n |, 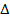 i –определитель, получаемый из определителя системы
i –определитель, получаемый из определителя системы  заменой i-го столбца столбцом свободных членов.
заменой i-го столбца столбцом свободных членов.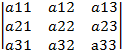 ,
,  ,
, ,
, 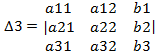
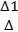 ,
,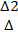

 ;у1
;у1 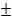 у2;z1
у2;z1 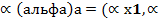 у1,∝z1)
у1,∝z1) =
=  =
= 




