
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема умножения вероятностей.Содержание книги
Поиск на нашем сайте О п р е д е л е н и е 1. Два события А и В называют независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет*. В противном случае события А и В называют зависимыми. П р и м е р 1. Пусть в урне находятся 2 белых и 2 черных шара. Пусть событие А — вынут белый шар. Очевидно, Р(А) = 1/2. После первого испытания вынутый шар кладется обратно в урну, шары перемешиваются и снова вынимается шар. Событие В – во втором испытании вынят белый шар- также имеет вероятность Р(В)=1/2. т.е события А и В – независимые. Предположим тепер, что вынутый шар в первом испытании не кладется обратно в урну. Тогда, если произошло событие А, т.е. в первом испытании вынут белый шар, то вероятность события В уменьшаеться и оказываеться равно одной трети, если в первом испытании был вынут черный шар, то вероятность события В увеличивается и становится равно двом третям. Итак, вероятность события В существенно зависит от того, произошло или не произошло событие А, в таких случаях событие А и В – зависимы. О п р е д е л е н и е 2. Пусть А и В – зависимые события. Условной вероятностью РА(В) события В называют вероятность события В, найденную в предположении, что событие А уже наступило. Так, в только что рассмотренном примере РА (В)=1,3. Условие независимости события В от события А можна записать в виде РА (В)=Р(В), А условие зависимости - в виде РА (В) Теорема 1. Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило: Р(АВ)=Р(А)РА (В) (1.6) Доказательство. Пусть из всего числа n элементарных событий k благоприятствуют событию А и пусть из этих k событий l благоприятствуют событию В, а, значит, и событию АВ. Тогда Р(АВ)=l/n=k/n*l/k=P(A)PA (B), Что и доказывает искомое равенство(1.6) Замечание. Применив формулу(1.6) к событию ВА, получим Р(ВА)-Р(В)РВ (А) (1.6’) Так как АВ=ВА(Параграф 1.1, п.2), то РВ (А)=Р(АВ)/Р(В), (1.7) а сравнивая (1.6) и (1.6’) получаем равенство Р(А)РА (В)=Р(В)РВ (А).
П ри м е р 2. Пусть в урне находятся 2 белых и 2 черных шара. Пусть событие А — вынут белый шар. Событие В — во втором испытании вынут белый шар. Рассмотрим тот случай, когда вынутый шар в первом испытании не кладется обратно в урну. Поставим следующий вопрос: какова вероятность вынуть первый и второй раз белые шары? По формуле (1.6) имеем: Р(АВ)=1/2. 1/3=1/6. П р и м е р 3. В терапевтическом отделении больницы 70% пациентов — женщины, а 21% — курящие мужчины. Наугад выбирают пациента. Он оказывается мужчиной. Какова вероятность того, что он курит? Пусть М означает, что пациент — мужчина, а К — что пациент курит. Тогда в силу условия задачи Р(М) = 0,3, а Р(МК) = 0,21. Поэтому с учетом формулы (1.6) искомая условная вероятность РМ (К) =Р(МК)/Р(М)=0,21/0,3=0,7. П р и м е р 4. В группе туристов 20% детей, причем 12% девочки. Наугад выбирают ребенка. Какова вероятность того, что это девочка? Какова -вероятность того, что это мальчик? Пусть А означает, что турист — ребенок, Ж— турист женского пола, М — мужского. Тогда по условию Р(А)=0,2, Р(ЖА)=0,12, Р(МА)=0,08. Следовательно, РА (Ж) =Р(ЖА)/Р(А)=0,12/0,2=0,6 РА (М)= Р(МА)/Р(А)=0,08/0,2=0,4 Задача (курение и случай заболевания легких). В группе обследуемых 1000 человек. Из них 600 курящих и 400 некурящих. Среди курящих 240 человек имеют те или иные заболевания легких. Среди некурящих легочных больных 120 человек. Являются ли курение и заболевание легких независимыми событиями? Р е ш е н и е. Пусть событие А — обследуемый курит, событие В —обследуемый страдает заболеванием легких. Тогда, согласно условию задачи, Р(В)=240+120/1000=0,36; РА (В)=240/600=2/5=0,4. Так как 0,36 П р и м е р 5. Предположим, что вероятности встретить реку, загрязняемую постоянным фактором А-Р(А), временным фактором В-Р(В) и обоими факторами- Р(АВ), равны соответственно 0,4; 0,1; 0,05. Найдем: 1)вероятность того, что река, загрязняемая временным фактором, будет к тому же загрязнена и постоянным фактором, т.е. РВ (А); 2)вероятность того, что река, загрязняемая постоянным фактором, будет еще загрязнена и временным фактором, т.е РА (В) Имеем, согласно(1.7): РВ (А)=Р(АВ)/Р(В) Откуда РВ (А)=0,05/0,4=0,5. Аналогично, используя формулу(1.6), находим РВ (А)=0,05/0,4=0,125 Теорема 2. Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий Р(АВ)=Р(А)Р(В) (1.9) Действительно, если А и В – независимые события, то РА (В)=Р(В) и формула (1.6) превращается в формулу (1.9) В случае независимых событий в совокупности эта теорема распространяется на любое конечное число их, т.е. имеет место равенство Р(А1 А2… Аn)=Р(А1)Р(А2)…Р(Аn) (1.10) Замечание 1. Если события А1 А2 Аn-независимы в совокупности, то и противоположные им события Ā1 Ā2 Ān также независимы в совокупности. П р и м е р 6. Найдем вероятность одновременного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым(событие В)-0,7. Событие А и В независимы, поэтому искомая вероятность Р(АВ)=0,7*0,8=0,56 П р и м е р 7. Вероятность выживания одной клетки в течение 20 минут Р=0,7. В пробирке с благоприятными для существования этих клеток условиями находятся только что разделившиеся две клетки. Какова вероятность тлго. Что через 20 минут они будут жизнеспособны? Пусть событие А – первая клетка жизнеспособна через 20 минут, событие В- вторая клетка жизнеспособна через 20 минут. Будем считать, что между клетками нет внутривидовой конкуренции, т. е. события А и В независимы. Событие, что обе клетки жизнеспособны, есть событие АВ. Р(АВ)=0,7. 0,7 =0,49. П р и м е р 8. Пусть у нас перемешаны записи нейронной активности 10 клеток из одной области мозга (у 5 клеток зарегистрирована активность, характерная для клеток (‘внимания,, у 5— другой вид активности) и 20 из другой области (у 15— активность типа клеток внимания, у 5— другого вида). Выясним, зависимы ли события А — *выбранная наугад запись сделана в первой области и В — на *выбранной наугад записи зарегистрирована активность, характерная для клеток *внимания.* Имеем Р (А)=10/30=I/3; Р(В)=20/30=2/3; Р (АВ) = 5/30 = 1/6; Р(АВ) ≠ Р(А)Р(В). Следовательно, события А и В зависимы. Теорема 3. Если события А1, А2,..., Аn,, независимы в совосупности, то вероятность наступления хотя бы одного из этих событий (т. е. вероятность суммы) вычисляется по формуле Р(А1 +А2 +... +Аn)= 1 - Р(Ā1)Р(Ā2)... Р(Ān). (1.11) Доказательство. Событие Ā1,Ā2... Ān состоит в том, что не произошло ни одно из событий А1 (і= 1, 2,..., n). Оно противоположно событию, состоящему в том, что произошло хотя бы одно из событий А1 т. е. сумме событий А1 + А2 +...+ Аn. Поэтому, согласно формуле (1.5), Р(А1 +А2 +... +Аn)+ Р(Ā1Ā2…Ān) Откуда Р(А1 +А2 +... +Аn)= 1 - Р(Ā1Ā2)... Ān). Но с учетом замечания 1 (п.2) и формулы (1.10) Р(А1 +А2 +... +Аn)= Р(Ā1)Р(Ā2)... Р(Ān). что и приводит к искомому равенству (1.11).
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 886; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.007 с.) |

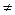 Р(В)
Р(В)


