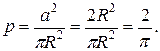Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение элементов комбинаторики к нахождению вероятностей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Комбинаторика — раздел математики, занимающийся вопросами о том, сколько комбинаций определенного типа можно получить из данных предметов (элементов). Как при решении задач с использованием классического определения вероятности, так и в дальнейшем могут нам понадобиться некоторые определения и формулы комбинаторики. Приведем наиболее употребительные из них. Определение 1. Размещениями из л различных элементов по т элементов (т Например, из трех элементов а, Ь, с можно составить по два элемента следующие размещения: ab, ас, be, bа, са, cb. Число А Пусть Пример 1. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Искомое число сигналов А Определение 2. Перестановками из л различных элементов называются размещения из этих л элементов по n. Перестановки можно рассматривать как частный случай размещений при т = п, поэтому общее число перестановок из n элементов равно Р Пример 2. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Искомое количество трехзначных чисел Р3 = 3! = 1 • 2 • 3 = 6. Определение 3. Сочетаниями из n различных элементов по т элементов называются комбинации, составленные из данных п элементов по т элементов, которые отличаются хотя бы одним элементом. Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов. Обозначим через С Рассмотрим все допустимые сочетания элементов аа]аа2...аа
Формулу (3) можно представить также в виде
C
которая также верна и при т = 0, если принять С Этой особенностью удобно пользоваться, когда т > Числа С
и поэтому часто называются биномиальными коэффициентами. Пример 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Искомое число способов
При решении задач комбинаторики можно использовать следующие правила: Правило суммы. Если некоторый элемент А может быть выбран из совокупности элементов т способами, а другой элемент В — п способами, то выбрать либо А, либо В можно т + п способами. Правило произведения. Если элемент А можно выбрать из совокупности элементов т способами и после каждого такого выбора элемент В можно выбрать п способами, то пара элементов (А, В) в указанном порядке может быть выбрана тп способами. Эти правила справедливы и для любого конечного числа элементов. Приведем, наконец, примеры применения формул комбинаторики к нахождению вероятностей событий. Пример 4. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно? Две последние цифры можно набрать Р(М) = Пример 5. Партия из 10 деталей содержит одну нестандартную. Какова вероятность, что при случайной выборке 5 деталей из этой партии все они будут стандартными (событие А)? Здесь число всех случайных выборок
Пример 6 (Задача о Генуэзской лотерее*). Разыгрывается 90 номеров, из которых выигрывают пять. По условию можно ставить ту или иную сумму на любой из 90 номеров или на любую совокупность двух, трех, четырех или пяти номеров. Если участник лотери ставил на один номер, то он получал при выиграше в 15 раз больше ставки; если на два номера (амбо), то в 270 раз больше; если на три номера (терн), то в 5500 раз больше; если на четыре номера (катерн) — в 75 000 раз больше; если на пять номеров (квин) — в 1 000 000 раз больше, чем ставка. Какова вероятность выигрыша в каждом из указанных пяти случаев? В первом случае вероятность выигрыша оказывалась
во втором, третьем, четвертом и пятом случаях вероятности выигрыша были соответственно равны:
§ 1.2. Геометрическая вероятность. Статистическое и аксиоматическое определения вероятности 1. Геометрическая вероятность. Классическое определение вероятности предполагает, что число всех элементарных событий конечно. Но на практике часто встречаются опыты, для которых множество таких событий бесконечно. Например, пусть на отрезке [0; 1] числовой прямой ставят наудачу точку. Что подсказывает нам интуиция о вероятностях событий «точка попала на правую половину Аналогично уясняется смысл выражения «точка поставлена наудачу в квадрат со стороной 1 (или в прямоугольник площадью 1)»,— это значит, что вероятность попадания точки на любую часть этого квадрата (или прямоугольника) равна площади этой части. В более сложных случаях (на плоскости) может оказаться, что при геометрической интерпретации получится такая картина: имеется фигура площадью s, и на нее наудачу ставится точка. Тогда вероятность попадания точки на часть этой фигуры, имеющую площадь q, оказывается равной q/s. Аналогично в трехмерном случае (в пространстве) здесь берется отношение соответствующих объемов. Такое определение вероятности получило название геометрического. Пример. В окружность вписан квадрат. В круг наудучу ставят точку. Какова вероятность того, что эта точка попадет в квадрат? Отношение площадей квадрата и круга дает искомую вероятность:
2. Относительная частота. Статистическое определение вероятности. Классическое определение вероятности оказывается непригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если.результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно. В таких случаях используется так называемое статистическое определение вероятности. Пусть произведено п испытаний, при этом некоторое событие А наступило т раз. Определение 1. Число т называется абсолютной частотой (или просто частотой) события А, а отношение Р*(А) = называется относительной частотой события А. Пример 1. При транспортировке из 10 000 арбузов испортилось 26. Здесь т = 26 — абсолютная частота испорченных арбузов, а
относительная. Результаты многочисленных опытов и наблюдений, многие из которых описаны, например, в работах [1—4], помогают заключить: при проведении серий из п испытаний, когда число п сравнительно мало, относительная частота Р*(А) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относительная частота Р*(А) = т/п приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения. Пример 2. Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484 (см. (4]). Эти частоты группируются около числа 0,5. Определение 2 (статистическое определение вероятности). Вероятностью события А в данном испытании называется число Р(А), около которого группируются значения относительной частоты при больших п. В условиях только что приведенного примера указанная вероятность равна 0,5. Пример 3. По данным шведской статистики, относительные частоты рождения девочек по месяцам одного года характеризуются следующими числами (расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473 (см. [2]). Эти частоты группируются около числа 0,482. Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико. Имеется огромный опытный материал по проверке последнего утверждения. Приведем еще один такой пример с бросанием монеты (см. [2]).
Здесь относительные частоты незначительно отличаются от числа 0,5, причем тем меньше, чем больше число испытаний. При 4040 испытаниях отклонение равно 0,008, а при 24000 — 0,0005. Таким образом, относительная частота события приближенно совпадает с его вероятностью в статистическом смысле, если число испытаний достаточно велико. С этой точки зрения величина m =nр представляет собой среднее значение числа появления события А при n испытаниях. При широких предположениях доказывается, что вероятности события в классическом и статистическом смысле совпадают между собой. 3. Аксиоматическое определение вероятности. В современных математических курсах вероятность определяется аксиоматически. При аксиоматическом построении теории вероятностей исходят из свойств вероятности событий, к которым применимо классическое или статистическое определение. Отдельные свойства вероятности известны из предыдущего изложения. Поэтому естественно принять следующие аксиомы. Аксиома 1. Каждому событию А поставлено в соответствие неотрицательное число Р(А), называемое его вероятностью. Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3. Вероятность суммы попарно несовместимых событий равна сумме вероятностей этих событий. Послёдняя аксиома называется аксиомой сложения вероятностей. Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем. Большая заслуга в аксиоматическом построении теории вероятностей принадлежит советскому математику А. Н. Колмогорову (1903—1987), работы которого положили начало созданию современной теории вероятностей как строгой математической науки [5]. Свойства вероятности
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 980; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.35.129 (0.008 с.) |

 ) называются комбинации, составленные из данных л элементов по т элементов, которые отличаются либо самими элементами, либо порядком элементов.
) называются комбинации, составленные из данных л элементов по т элементов, которые отличаются либо самими элементами, либо порядком элементов. размещений из n элементов а1, а2, ..., а
размещений из n элементов а1, а2, ..., а  по т равно
по т равно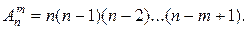 (1.1)
(1.1) — всевозможные размещения, содержащие т элементов. Будем эти размещения строить последовательно. Сначала определим
— всевозможные размещения, содержащие т элементов. Будем эти размещения строить последовательно. Сначала определим 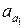 — первый элемент размещения. Очевидно,.из данной совокупности п элементов его можно выбрать л различными способами. После выбора первого элемента
— первый элемент размещения. Очевидно,.из данной совокупности п элементов его можно выбрать л различными способами. После выбора первого элемента  остается n - 1 способов выбора и т. д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому общее число размещений равно указанному произведению (1.1).
остается n - 1 способов выбора и т. д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому общее число размещений равно указанному произведению (1.1).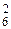 - 6 • 5 = 30.
- 6 • 5 = 30. 2
2 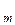 . Делая в каждом из них m! возможных перестановок их элементов, очевидно, получим общее число рамещений из п элементов по т. Таким образом, С
. Делая в каждом из них m! возможных перестановок их элементов, очевидно, получим общее число рамещений из п элементов по т. Таким образом, С  ; отсюда
; отсюда (1.3)
(1.3)
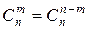
 = 1.
= 1. .
.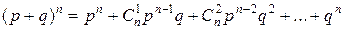

 способами, а благоприятствовать событию М (цифры набраны правильно) будет только один способ. Поэтому
способами, а благоприятствовать событию М (цифры набраны правильно) будет только один способ. Поэтому
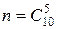 , а число выборок, благоприятствующих событию А, есть т = С
, а число выборок, благоприятствующих событию А, есть т = С 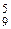 . Таким образом, искомая вероятность
. Таким образом, искомая вероятность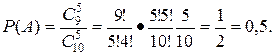


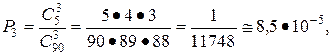


 отрезка» и «точка попала на левую половину отрезка»? Поскольку точка ставится наудачу, то естественно считать эти события равновероятными — вероятность каждого 0,5 (поскольку это противоположные события). Ну, а если мы разделим отрезок на 10 равных отрезков и рассмотрим события «точка попала на левый отрезок», «точка попала на второй слева отрезок»,..., «точка попала на правый отрезок»? Это опять равновероятные события. А вероятность каждого из них оказывается равной 0,1, поскольку это совокупность всех элементарных событий нашего опыта. Поставим теперь вопрос: «Какова вероятность попадания точки на отрезок [0,3; 0,7]?» Поскольку этому событию благоприятствуют четыре из указанных выше элементарных события, то искомая вероятность равна 0,4, т. е. длине отмеченного отрезка. В общем случае смысл выражения «точка поставлена наудачу на отрезок длины 1» состоит в том, что вероятность попадания точки на часть этого отрезка длины l равна этому числу l (если вместо отрезка [0; 1] взять отрезок [0; s], s>l, то искомая вероятность будет равна l/s).
отрезка» и «точка попала на левую половину отрезка»? Поскольку точка ставится наудачу, то естественно считать эти события равновероятными — вероятность каждого 0,5 (поскольку это противоположные события). Ну, а если мы разделим отрезок на 10 равных отрезков и рассмотрим события «точка попала на левый отрезок», «точка попала на второй слева отрезок»,..., «точка попала на правый отрезок»? Это опять равновероятные события. А вероятность каждого из них оказывается равной 0,1, поскольку это совокупность всех элементарных событий нашего опыта. Поставим теперь вопрос: «Какова вероятность попадания точки на отрезок [0,3; 0,7]?» Поскольку этому событию благоприятствуют четыре из указанных выше элементарных события, то искомая вероятность равна 0,4, т. е. длине отмеченного отрезка. В общем случае смысл выражения «точка поставлена наудачу на отрезок длины 1» состоит в том, что вероятность попадания точки на часть этого отрезка длины l равна этому числу l (если вместо отрезка [0; 1] взять отрезок [0; s], s>l, то искомая вероятность будет равна l/s).