
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет по устойчивости полок и стенок элементов, не подкрепленных ребрами жесткостиСодержание книги
Поиск на нашем сайте
8.44 Расчет по устойчивости полок и стенок прокатных и. составных сварных центрально- и виецентрснно сжатых, а также сжато-изгибаемых и изгибаемых элементов постоянного поперечного сечения, не подкрепленных ребрами жесткости (рисунок 8.1), следует выполнять по теории призматических складчатых оболочек.
Рисунок 8.1 - Схемы расчетных сечений элементов, не подкрепленных ребрами жесткости 8.45 Устойчивость полок и стенок элементов, не подкрепленных ребрами жесткости, при среднем касательном напряжении, не превышающем 0,2σ x, допускается обеспечивать назначением отношения высоты стенки (h, hw) или ширины полки (bf, bh,) к толщине (t, tw, tf, th) не более Коэффициент α следует определять: для пластинок шириной bh, h, опертых по одной стороне (рисунок 8.1, б - e), - по формуле
для пластинок шириной hw, bf, опертых по двум сторонам (рисунок 8.1, a, б, г), - по формуле
В формулах (8.55) и (8.56):
ξ - коэффициент, определяемый (для сечений брутто) по формуле
где σ х, Таблица 8.22
Приведенное критическое напряжение σ х , cr , еf для пластинки следует определять но формулам таблицы 8.23 в зависимости от критических напряжений σ х , cr , еf за которые следует принимать действующие напряжения σ x / m (здесь m - коэффициент условий работы, принимаемый по таблице 8.15). Таблица 8.23
Расчет по устойчивости полок и стенок элементов, подкрепленных ребрами жесткости 8.46 Расчет по устойчивости полок и стенок элементов, подкрепленных ребрами жесткости, следует выполнять по теории призматических складчатых оболочек, укрепленных поперечными диафрагмами. Допускается выполнять расчет по устойчивости пластинок, полок и стенок указанных элементов согласно приложению X. 8.47 Устойчивость пластинок ортотропных плит допускается обеспечивать назначением отношения их толщины к ширине в соответствии с 8.45, при этом: для полосовых продольных ребер коэффициент α следует определять по формуле (8.55) при коэффициенте защемления для участка листа ортотропной плиты между соседними продольными полосовыми ребрами коэффициент α следует определять по формуле (8.56) при коэффициенте защемления
Рисунок 8.2 - Схемы расчетных сечений пластинок ортотропных плит. Расчетные длины 8.48 Расчетные длины lef элементов главных ферм, за исключением элементов перекрестной решетки, следует принимать по таблице 8.24. Таблица 8.24
8.49 Расчетную длину lef элемента, по длине которого действуют разные сжимающие усилия N 1 и N 2 (причем N 1 > N 2), из плоскости фермы (с треугольной решеткой со шпренгелем или полураскосной и т.д.) следует вычислять по формуле
где l 1 - расстояние между узлами, закрепленными от смещения из плоскости фермы. Расчет по устойчивости в этом случае следует выполнять на усилие N 1. Применение формулы (8.58) допускается при растягивающей силе N 2, в этом случае значение N 2 следует принимать со знаком «минус», а lef > 0,5 l 1. 8.50 Расчетные длины lef элементов перекрестной решетки главной фермы следует принимать: в плоскости фермы - равными 0,8 l, где l - расстояние от центра узла фермы до точки их пересечения; из плоскости фермы: для сжатых элементов - по таблице 8.25; для растянутых элементов - равными полной геометрической длине элемента (lef = l 1, где l 1 см. таблицу 8.24). Таблица 8.25
8.51 При проверке общей устойчивости балки расчетную длину сжатого пояса следует принимать равной: расстоянию между узлами фермы продольных связей - при наличии продольных связей в зоне верхних и нижних поясов и поперечных связей в опорных сечениях; расстоянию между фермами поперечных связей - при наличии продольных связей только в зоне растянутых поясов, при этом фермы поперечных связей должны быть центрированы с узлами продольных связей, а гибкость поясов указанных ферм не должна превышать 100. пролету балки - при отсутствии в пролете продольных и поперечных связей; расстоянию от конца консоли до ближайшей плоскости поперечных связей за опорным сечением консоли - при монтаже пролетного строения внавес или продольной надвижкой. 8.52 Расчетную длину lef сжатого пояса главной балки или фермы «открытого» пролетного строения, не имеющего продольных связей по этому поясу, следует определять, как правило, из расчета по устойчивости стержня на упругих опорах сжатого переменной по длине продольной силой. Допускается определять указанную расчетную длину по формуле
где l - длина пояса, равная расчетному пролету для балок и ферм с параллельными поясами, полной длине пояса для балок с криволинейным верхним поясом и ферм с полигональным верхним поясом; μ - коэффициент расчетной длины. Коэффициент расчетной длины μ для поясов балок и ферм с параллельными поясами, а также для фермы с полигональным или балки с криволинейным верхним поясом следует определять по таблице 8.26, при этом наибольшее перемещение 5 следует принимать для рамы, расположенной посредине пролета. Таблица 8.26
8.53 Расчет арок по устойчивости выполняется с учетом совместной работы арок и элементов проезжей части и поддерживающих ее элементов. При проверке общей устойчивости арки сплошного постоянного сечения допускается определять расчетную длину lеf в ее плоскости по формуле
где l - длина пролета арки; α = f / l - коэффициент (здесь f - стрела подъема арки); ξ - коэффициент, принимаемый по таблице 8.27. Значение ξ для двухшарнирной арки переменного сечения при изменении ее момента инерции в пределах ± 10 % среднего его значения по длине пролета допускается определять по поз. 4 таблицы 8.27, принимая при этом EIbog в четверти пролета. Во всех случаях расчетная длина lеf арки в ее плоскости должна быть не менее расстояния между узлами прикрепления стоек или подвесок. Таблица 8.27
Таблица 8.28
8.54 Расчетную длину lеf элементов продольных и поперечных связей с любой решеткой, кроме крестовой, следует принимать равной: в плоскости связей - расстоянию l 2 между центрами прикреплений элементов связей к главным фермам или балкам, а также балкам проезжей части; из плоскости связей - расстоянию l 3 между точками пересечения оси элемента связей с осями крайних рядов болтов прикрепления фасонок связей к главным фермам или балкам, а также балкам проезжей части. Расчетную длину lеf перекрещивающихся элементов связей следует принимать: в плоскости связей - равной расстоянию от центра прикрепления элемента связей к главной ферме или балке, а также балке проезжей части - до точки пересечения осей связей; из плоскости связей: для растянутых элементов - равной l 3, для сжатых элементов - по таблице 8.25 принимая при этом за l расстояние от точки пересечения оси элемента связей с осью крайнего ряда болтов прикрепления фасонок связей до точки пересечения осей элементов связей, за l 1 - расстояние l 3. Для элементов связей с любой решеткой, кроме крестовой, из одиночных уголков расчетную длину lef следует принимать равной расстоянию l между крайними болтами прикреплений их концов. При крестовой решетке связей lеf = 0,6 l. Радиус инерции сечений следует принимать минимальным (i = i min). 8.55 В сплошностенчатых балках расчетную длину lef опорных стоек, состоящих из одного или нескольких опорных ребер жесткости и примыкающих к ним участков стенки, следует определять по формуле
где μ - коэффициент расчетной длины; 1c - длина опорной стойки балки, равная расстоянию от верха дом кратной балки до верхнего пояса или до ближайшего узла поперечных связей. Коэффициент расчетной длины μ опорной стойки следует определять по формуле
здесь где Ic - момент инерции сечения опорной стойки относительно оси, совпадающей с плоскостью стенки; Ir, lr - соответственно момент инерции сечения и длина распорки поперечных связей; в «открытых» пролетных строениях в формуле (8.62) следует принимать n = 0. При определении площади, момента инерции и радиуса инерции опорной стойки с одним ребром жесткости в состав ее сечения следует включать кроме опорного ребра жесткости примыкающие к нему участки стенки шириной b 1 = ξ1 t (здесь t - толщина сечения, ξ1 - коэффициент, принимаемый по таблице 8.29).
Таблица 8.30
|
При определении площади, момента инерции и радиуса инерции опорной стойки с несколькими, ребрами жесткости при расстояниях между ними b 2 = ξ2 t (здесь ξ2 - коэффициент, принимаемый по таблице 8.30) в состав ее сечения следует включать все указанные ребра жесткости, участки стенки между ними, а также примыкающие с внешней стороны к крайним ребрам жесткости участки стенки шириной b 1 = ξ1 t, где ξ1 следует принимать по таблице 8.29.
|
| Поделиться: |


 (здесь α - коэффициент, σ x, σ x , cr , ef приведенное критическое напряжение).
(здесь α - коэффициент, σ x, σ x , cr , ef приведенное критическое напряжение).
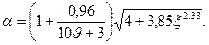
 - коэффициент защемления пластинки, определяемый по формулам таблицы 8.22;
- коэффициент защемления пластинки, определяемый по формулам таблицы 8.22;
 - максимальное и минимальное продольные нормальные напряжения по продольным границам пластинки, положительные при сжатии, определяемые по формулам (8.4) - (8.25) при невыгодном для устойчивости пластинки загружении, при этом коэффициенты æ, æ x, æ y, ψ, ψ x, ψ y, следует принимать равными 1,0.
- максимальное и минимальное продольные нормальные напряжения по продольным границам пластинки, положительные при сжатии, определяемые по формулам (8.4) - (8.25) при невыгодном для устойчивости пластинки загружении, при этом коэффициенты æ, æ x, æ y, ψ, ψ x, ψ y, следует принимать равными 1,0.






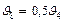




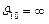
 Примечания
1 При Отрицательном значении знаменателя в формулах таблицы 8.22, а также при равенстве его нулю следует принимать
Примечания
1 При Отрицательном значении знаменателя в формулах таблицы 8.22, а также при равенстве его нулю следует принимать 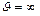 .
2 Для углового сечения с отношением bh / h. не указанным в таблице 8.22. значение
.
2 Для углового сечения с отношением bh / h. не указанным в таблице 8.22. значение  , следует определять по интерполяции, при этом для bh / h = 1 значение
, следует определять по интерполяции, при этом для bh / h = 1 значение  следует принимать рапным 100.
следует принимать рапным 100.


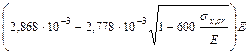
 и свесе полки тавра bh, (рисунок 8.2, а), равном 0,5 hw, при ξ2 th ≥ hw или ξ1 th при ξ2 th < hw;
и свесе полки тавра bh, (рисунок 8.2, а), равном 0,5 hw, при ξ2 th ≥ hw или ξ1 th при ξ2 th < hw; , высоте стенки hw, равной расстоянию между продольными ребрами, и свесе полки bh, равном высоте продольного ребра (рисунок 8.2, б), но не более ξ1 th; здесь ξ1 и ξ2 - коэффициенты, определяемые по 8.55.
, высоте стенки hw, равной расстоянию между продольными ребрами, и свесе полки bh, равном высоте продольного ребра (рисунок 8.2, б), но не более ξ1 th; здесь ξ1 и ξ2 - коэффициенты, определяемые по 8.55.


 где d - расстояние между рамами, закрепляющими пояс от поперечных горизонтальных перемещений;
δ - наибольшее горизонтальное перемещение узла-рамы (исключая опорные рамы) от силы F = 1;
Im - среднее (по длине пролета) значение момента инерции сжатого пояса балки (фермы) относительно вертикальной оси.
Примечания
1 Если полученная по данным таблицы 8.26 расчетная длина lef < l,3 d. то се определяют из расчета по устойчивости стержня на упругих опорах.
2 Для промежуточных значений ξ, коэффициент μ определяют по линейной интерполяции.
где d - расстояние между рамами, закрепляющими пояс от поперечных горизонтальных перемещений;
δ - наибольшее горизонтальное перемещение узла-рамы (исключая опорные рамы) от силы F = 1;
Im - среднее (по длине пролета) значение момента инерции сжатого пояса балки (фермы) относительно вертикальной оси.
Примечания
1 Если полученная по данным таблицы 8.26 расчетная длина lef < l,3 d. то се определяют из расчета по устойчивости стержня на упругих опорах.
2 Для промежуточных значений ξ, коэффициент μ определяют по линейной интерполяции.

 Ibat и Ibog - моменты инерции сечений соответственно балки жесткости и арки.
* При отношении жесткостей затяжки и арки, большем 0.8. расчетная длина арки определяется как для двухшарнирной арки с неразрезной балкой жесткости, соединенной с аркой стойками.
Ibat и Ibog - моменты инерции сечений соответственно балки жесткости и арки.
* При отношении жесткостей затяжки и арки, большем 0.8. расчетная длина арки определяется как для двухшарнирной арки с неразрезной балкой жесткости, соединенной с аркой стойками.





