
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициенты для расчета по устойчивости стержней и балокСодержание книги
Поиск на нашем сайте
Таблица Ф.1
Таблица Ф.2
Таблица Ф.3
Коэффициенты влияния формы сечения η Коэффициенты влияния формы сечения η при определении приведенного относительного эксцентриситета по формуле ееf = η erel следует принимать по СП 16.13330, вычисляя при этом условную гибкость
где αr - коэффициент, принимаемый по таблице Ф.4, при этом m = erel. Таблица Ф.4
Приложение X Расчет по устойчивости полок и стенок элементов, Х.1 Прямоугольные отсеки полок и стенок (далее - пластинки), заключенные между подкрепляющими их по контуру ортогональными деталями (ребра жесткости, полка для стенки и стенка для полки), следует рассчитывать по устойчивости. При этом расчетными размерами и параметрами проверяемой пластинки являются: α - длина пластинки, равная расстоянию между осями поперечных ребер жесткости; hef - расчетная ширина пластинки, равная: при отсутствии продольных ребер жесткости у прокатного или сварного элемента -расстоянию между осями поясов hw или осями стенок коробчатого сечения bf, то же, у составного элемента с болтовыми соединениями - расстоянию между ближайшими рисками поясных уголков; при наличии продольных ребер жесткости у сварного или прокатного элемента -расстоянию от оси пояса (стенки) до оси крайнего продольного ребра жесткости h 1 и hn или расстоянию между осями соседних продольных ребер жесткости hi (i = 2; 3; 4; 5...); то же, у составного элемента с болтовыми соединениями - расстоянию от оси крайнего ребра жесткости до ближайшей риски поясного уголка h\ и h„ или расстоянию между осями соседних продольных ребер жесткости hi (i = 2; 3; 4; 5...); t - толщина проверяемой пластинки; t 1, b 1 - толщина и расчетная ширина листа, ортогонального к проверяемой пластинке; в расчетную ширину этого листа в двутавровом сечении следует включать (в каждую сторону от проверяемой пластинки) участок листа шириной ξ1 t 1, но не более ширины свеса, а в коробчатом сечении - участок шириной 1/2 ξ2 t 1, но не более половины расстояния между стенками коробки (здесь коэффициенты ξ1 и ξ2 следует определять по 8.55);
В случае если проверяемая пластинка примыкает к пакету из двух листов и более, за t 1 и b 1 принимаются толщина и расчетная ширина первого листа пакета, непосредственно примыкающего к указанной пластинке. Таблица Х.1
Х.2 Расчет по устойчивости пластинок следует выполнять с учетом всех компонентов напряженного состояния - σ х, σ y, σ xy. Напряжения σ х, σ y, σ xy следует вычислять в предположении упругой работы материала по сечению брутто без учета коэффициентов продольного изгиба. Максимальное σ х и минимальное
где y max, ymin - максимальное и минимальное расстояния от нейтральной оси до продольной границы пластинки (с учетом знака); Мm - среднее значение изгибающего момента в пределах отсека при μ ≤ 1; если длина отсека больше его расчетной ширины, то Мm следует вычислять для более напряженного участка длиной, равной ширине отсека; если в пределах отсека момент меняет знак, то Мm следует, вычислять на участке отсека с моментом одного знака. Среднее касательное напряжение х„ следует определять: при отсутствии продольных ребер жесткости - по формуле
где
где при их наличии - по формуле
В формулах (Х.4) и (Х.5): Qm - среднее значение поперечной силы в пределах отсека, определяемое так же, как и Мm; τ1, τ2 - значения касательных напряжений на продольных границах пластинки, определяемые по формуле (Х.3) при замене S max соответствующими значениями S. Поперечное нормальное напряжение σ y (положительное при сжатии), действующее на внешнюю кромку крайней пластинки, следует определять: от подвижной нагрузки - по формуле
где Р - распределенное давление на внешнюю кромку крайней пластинки. определяемое по обязательному приложению К; от сосредоточенного давления силы F - по формуле
где lef - условная длина распределения нагрузки. Условную длину распределения нагрузки lef следует определять: при передаче нагрузки непосредственно через пояс балки или через рельс и пояс - по формуле
где с - коэффициент, принимаемый для сварных и прокатных элементов равным 3,25, для элементов с соединениями на высокопрочных болтах - 3,75, на обычных болтах - 4,5; l - момент инерции пояса балки или сумма моментов инерции пояса и рельса; при передаче нагрузки от катка через рельс, деревянный лежень и пояс балки - равной 2 h (где h - расстояние от поверхности рельса до кромки пластинки), но не более расстояния между соседними катками. Поперечные нормальные напряжения σ y на границе второй и последующих пластинок следует определять, как правило, по теории упругости. Допускается их определять: при нагрузке, распределенной по всей длине пластинки, - по формуле
при сосредоточенной нагрузке - по формуле
В формулах (Х.9) и (X.10):
где h 0 - часть высоты стенки, равная расстоянию от оси нагруженного пояса в сварных и прокатных балках или от ближайшей риски поясного уголка в балках с болтовыми соединениями до границы проверяемой пластинки; hw - полная высота стенки. Х.3 Критические напряжения σ xcr, σ ycr, τ xy,cr, σ x.cr.ef, σy.cr.ef, τ xy.cr.tf следует определять в предположении действия только одного из рассматриваемых напряжений σ х, σ у, τ хy. Приведенные критические напряжения σ x.cr.ef, σy.cr.ef, τ xy.cr.ef в общем случае вычисляют в предположении неограниченной упругости материала на основе теории устойчивости первого 'рода (бифуркация форм равновесия) для пластинчатых систем. Значения приводимых в таблицах Х.2, Х.4 - Х.13 параметров для определения критических напряжений в пластинках допускается находить по линейной интерполяции. Х.4 Расчет по устойчивости стенки сплошных изгибаемых элементов, имеющей только поперечные ребра жесткости, следует выполнять по формуле
где σ xcr, σ ycr - критические нормальные напряжения соответственно продольное и поперечное; τ xy,cr - критическое касательное напряжение; ω1 - коэффициент, принимаемый по таблице Х.2;
Таблица Х.2
Критические напряжения σ xcr, σ ycr, τ xy,cr следует определять по формулам таблицы Х.3 в зависимости от приведенных критических напряжений σ x.cr.ef, σy.cr.ef, τ xy.cr.ef вычисляемых по Х.4.1 - Х.4.3. При этом τ xy,cr определяется по формулам для σ xcr с подстановкой в них соотношений:
Таблица Х.3
Х.4.1 Приведенное критическое продольное нормальное напряжение для пластинок стенки изгибаемого элемента следует определять по формуле
где χ - коэффициент упругого защемления стенки, принимаемый для элементов с болтовыми соединениями равным 1,4, для сварных элементов - по таблице Х.4; ε - коэффициент, принимаемый по таблице Х.5. Таблица Х.4
Таблица Х.5
Х.4.2 Приведенное критическое поперечное нормальное напряжение σy.cr.ef Для пластинок стенки изгибаемого элемента следует определять по формуле
где ξ - коэффициент, принимаемый равным единице при нагрузке, распределенной по всей длине пластинки, и по таблице Х.6 - при сосредоточенной нагрузке; χ - коэффициент упругого защемления стенки, принимаемый по таблице Х.7; z - коэффициент, принимаемый по таблице Х.8. Таблица Х.6
Таблица Х.7
Таблица Х.8
Х.3 Приведенное критическое касательное напряжение τ xy.cr.ef для пластинок стенок изгибаемого элемента следует определять по формуле
где d - меньшая сторона отсека (а или hef); μ1 - коэффициент, принимаемый равным μ при а > hef и 1/μ при a < hef, χ - коэффициент упругого защемления стенки, принимаемый равным единице для элементов с болтовыми соединениями и по таблице Х.9 - для сварных элементов. Таблица Х.9
Х.5 Расчет по устойчивости пластинок стенки сплошных изгибаемых элементов, имеющих поперечные ребра и одно продольное ребро в сжатой зоне, следует выполнять:
где ω1 - коэффициент, принимаемый по таблице Х.2; σ х, σ y, τ ху - напряжения, определяемые по Х.2; σ x.cr, σy.cr, τ xy.cr - критические напряжения, определяемые Х.4; второй пластинки - между растянутым поясом и продольным ребром - по формуле (Х.11), принимая при этом ω2 = 1. Х.5.1 Приведенное критическое продольное нормальное напряжение σ x.cr.ef следует определять по формуле (Х.12), при этом коэффициент упругого защемления χ следует принимать: первой пластинки: элементов с болтовыми соединениями - χ = 1,3; таких же и сварных элементов при объединении с железобетонной плитой – χ = 1,35; прочих сварных элементов - по таблице Х.10; второй пластинки – χ = 1. Таблица Х.10
Х.5.2 Приведенное критическое поперечное нормальное напряжение σ x.cr.ef в первой пластинке следует определять по формуле
где i - коэффициент, принимаемый равным 1,0 при μ = a / h 1 ≥ 0,7 и 2,0 при 0,7 > μ > 0,4; χ - коэффициент упругого защемления, принимаемый по таблице X.11 для элементов, объединенных с железобетонной плитой, и для балок с болтовыми соединениями, по таблице Х.12 - для сварных балок. Таблица Х.11
Таблица Х.12
Приведенное критическое поперечное нормальное напряжение σ x.cr.ef при воздействии сосредоточенной нагрузки, когда действующие напряжения определяются по формуле (Х.7), следует вычислять по формуле (Х.16) с умножением на коэффициент 1,55; если при этом а > 2 h 1 + 2 1ef то надлежит принимать К Приведенное критическое поперечное нормальное напряжение σ x.cr.ef во второй пластинке следует определять по формуле (Х.13), при этом следует принимать: χ = 1; z - по таблице Х.8; ξ - по таблице Х.6 при ρ = 0,35. Х.5.3 Приведенное критическое касательное напряжение τ xy.cr.ef следует определять по формуле (Х.14), при этом для первой пластинки вместо коэффициента защемления χ должен быть принят коэффициент Х.6 Расчет по устойчивости пластинок стенки сплошных изгибаемых элементов, имеющих поперечные ребра и несколько продольных ребер жесткости, следует выполнять: первой пластинки - между сжатым поясом и ближайшим ребром - по формуле (Х.15) и формулам (Х.12), (Х.16) и (Х.14) для σ x.cr.ef, σy.cr.ef, τ xy.cr.ef соответственно; для последующих сжатых пластинок - по формулам для первой пластинки, принимая коэффициент защемления χ = 1; для сжато-растянутой пластинки - по формуле (Х.11), принимая ω1 = 1, и формулам (Х.12), (Х.16) и (Х.14) для к σ x.cr.ef, σy.cr.ef, τ xy.cr.ef как для второй пластинки по Х.5. Расчет по устойчивости пластинки растянутой зоны стенки следует выполнять по формуле
где σy.cr.f, τ xy.cr - критические поперечное нормальное и касательное напряжения, определяемые по σy.cr.ef, τ xy.cr.ef согласно указаниям Х.4, при этом приведенное критическое поперечное нормальное напряжение σy.cr.ef следует определять по формуле
где δ - коэффициент, принимаемый по таблице Х.13. Таблица Х.13
Приведенное критическое касательное напряжение τ xy.cr.ef следует определять: для пластинки, примыкающей к растянутому поясу, - по формуле
для промежут
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.35.116 (0.01 с.) |

 по формуле
по формуле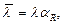
 здесь σ x и
здесь σ x и  определяются по Х.2;
определяются по Х.2;
 , здесь β - коэффициент, принимаемый по таблице X.1.
, здесь β - коэффициент, принимаемый по таблице X.1. продольные нормальные напряжения (положительные при сжатии) по продольным границам пластинки следует определять по формулам:
продольные нормальные напряжения (положительные при сжатии) по продольным границам пластинки следует определять по формулам:







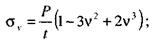



 - коэффициент, вводимый при расчете автодорожных и городских мостов при hw / t > 100.
- коэффициент, вводимый при расчете автодорожных и городских мостов при hw / t > 100.




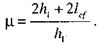
 , для второй пластинки - χ = 1.
, для второй пластинки - χ = 1.





