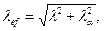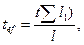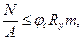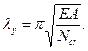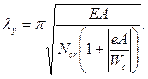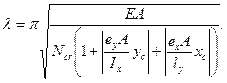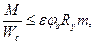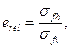Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет на прочность и ползучесть стальных канатовСодержание книги
Поиск на нашем сайте
8.33 Расчет по прочности стальных канатов гибких несущих элементов в вантовых и висячих мостах, а также напрягаемых элементов предварительно напряженных конструкций следует выполнять по формуле
где Rdh - расчетное сопротивление канатов; m - коэффициент условий работы, принимаемый по таблице 8.15; m 1 - коэффициент условий работы, определяемый по приложению У. Расчетное сопротивление Rdh для канатов и пучков из параллельно уложенных высокопрочных проволок определяется по формуле (8.3), для канатов одинарной свивки и закрытых несущих - по формулам
где [Σ Pun ] - значение разрывного усилия каната в целом, указанное в государственном стандарте или технических условиях; γ m =. 1,6 согласно 8.17; Σ Pun - сумма разрывных усилий всех проволок в канате; k - коэффициент агрегатной прочности витого каната, определяемый по таблице 8.20. Таблица 8.20
8.34 Продольную ползучесть ε pe,x стальных оцинкованных витых канатов с металлическим сердечником - одинарной свивки и закрытых несущих, подвергнутых предварительной вытяжке, следует определять по формуле
где σ - напряжение в канате от усилия, подсчитанного от воздействия нормативных постоянных нагрузок и 1/3 нормативной временной нагрузки;
e - основание натуральных логарифмов. 8.35 Поперечную ползучесть ε pl,y канатов, указанных в 8.34, следует определять по формуле
Расчеты по устойчивости 8.36 Расчет при плоской форме потери устойчивости сплошностенчатых элементов замкнутого и открытого сечений, подверженных центральному сжатию, сжатию с изгибом и внецентренному сжатию при изгибе в плоскости наибольшей гибкости, следует выполнять по формуле
где φ - коэффициент продольного изгиба, определяемый по таблицам Ф.1 - Ф.3 приложения Ф в зависимости от гибкости элемента λ и приведенного относительного эксцентриситета еrf; m - здесь и в 8.38 - 8.41 - коэффициент условий работы, принимаемый по таблице 8.15. Гибкость элемента λ следует определять по формуле
где lef - расчетная длина; i - радиус инерции сечения относительно оси, перпендикулярной плоскости наибольшей гибкости (плоскости изгиба). Приведенный относительный эксцентриситет еef следует определять по формуле
где η - коэффициент влияния формы сечения, определяемый по приложению Ф; erel = е /ρ - относительный эксцентриситет плоскости изгиба, принимаемый при центральном сжатии равным нулю; е - действительный эксцентриситет силы N при внецентренном сжатии и расчетный эксцентриситет при сжатии с изгибом; ρ - ядровое расстояние. Расчетный эксцентриситет е в плоскости изгиба при сжатии с изгибом следует определять по формуле
где N, М - расчетные значения продольной силы и изгибающего момента. Ядровое расстояние ρ по направлению эксцентриситета следует определять по формуле
где Wc - момент сопротивления сечения брутто, вычисляемый для наиболее сжатого волокна. Расчетные значения продольной силы N и изгибающего момента М в элементе следует принимать для одного и того же сочетания нагрузок из расчета системы по недеформированной схеме в предположении упругих деформаций стали. При этом значения М следует принимать равными: для элементов постоянного сечения рамных систем - наибольшему моменту в пределах длины элемента; для элементов с одним защемленным, а другим свободным концом - моменту в заделке, но не менее момента в сечении, отстоящем на треть длины элемента от заделки; для сжатых поясов ферм, воспринимающих внеузловую нагрузку, - наибольшему моменту в пределах средней трети длины панели пояса, определяемому из расчета пояса как упругой неразрезной балки; для сжатых стержней с шарнирно опертыми концами и сечениями, имеющими одну ось симметрии, совпадающую с плоскостью изгиба, - моменту, определяемому по формулам таблицы 8.21. Для сжатых стержней с шарнирно опертыми концами и сечениями, имеющими две оси симметрии, расчетные значения приведенных относительных эксцентриситетов e ef следует определять по СП 16.13330, принимая при этом mcf равным e ef и m ef 1 равным e ef 1, определяемому по формуле
где М 1 - больший из изгибающих моментов, приложенных на шарнирно опертых концах сжатого стержня указанного типа. Таблица 8.21
8.37 Расчет при плоской форме потери устойчивости сквозных элементов замкнутого сечения, ветви которых соединены планками или перфорированными листами, при центральном сжатии, сжатии с изгибом и внецентренном сжатии следует выполнять: элемента в целом в плоскости действия изгибающего момента или предполагаемого (при центральном сжатии) изгиба, перпендикулярной плоскости планок или перфорированных листов, - по формуле (8.35); элемента в целом в плоскости действия изгибающего момента или предполагаемого (при центральном сжатии) изгиба, параллельной плоскости планок или перфорированных листов, - по формуле (8.35) с определением коэффициента продольного изгиба φ по таблицам Ф.1 -Ф.3 приложения Ф в зависимости от приведенной гибкости λ ef; отдельных ветвей - по формуле (8.35) в зависимости от гибкости ветви λα. Гибкость ветви λα следует определять по формуле (8.36), принимая за расчетную длину lef расстояние между приваренными планками (в свету) или расстояние между центрами крайних болтов соседних планок, или равное 0,8 длины отверстия в перфорированном листе и за i - радиус инерции сечения ветви относительно собственной оси, перпендикулярной плоскости планок или перфорированных листов. Приведенную гибкость сквозного элемента λ el в плоскости соединительных планок и перфорированных листов следует определять по формуле
где λ - гибкость элемента в плоскости соединительных планок или перфорированных листов, определяемая по формуле 8.36); λα - гибкость ветви. При подсчете площади сечения, момента инерции и радиуса инерции элемента следует принимать эквивалентную толщину tef определяя ее: для перфорированных листов шириной b, длиной l и толщиной t - по формуле
где А = bl - площадь листа до образования перфораций; Σ A 1 - суммарная площадь всех перфораций на поверхности листа; для соединительных планок толщиной t - по формуле
где Σ l 1 - сумма длины всех планок элемента (вдоль элемента); l - длина элемента. Сквозные элементы из деталей, соединенных вплотную или через прокладки, следует рассчитывать как сплошные, если наибольшие расстояния между болтами, приваренными планками (в свету) или между центрами крайних болтов соседних планок не превышают: для сжатых элементов – 40 i; для растянутых элементов – 80 i. Здесь радиус инерции i уголка или швеллера следует принимать для составных тавровых или двутавровых сечений относительно оси, параллельной плоскости расположения прокладок, для крестовых сечений -минимальный. При этом в пределах длины сжатого элемента должно быть не менее двух прокладок. 8.38 Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых элементов открытого сечения с моментами инерции Ix > Iy, подверженных центральному сжатию силой N, следует выполнять по формуле
где φc - коэффициент продольного изгиба, определяемый по таблицам Ф.1 - Ф.3 приложения Ф при eef = 0 и
8.39 Расчет на изгибно-крутильную устойчивость сплошностенчатых элементов замкнутого и Открытого сечений с моментами инерции Ix > Iy, подверженных сжатию с изгибом и внецентренному сжатию в плоскости наименьшей гибкости, совпадающей с плоскостью симметрии и осью у, следует выполнять по формуле
где е - действительный эксцентриситет силы N при внецентренном сжатии и расчетный эксцентриситет е = M / N при сжатии с изгибом; Wc - момент сопротивления сечения брутто, вычисляемый для наиболее сжатого волокна; φ с - коэффициент продольного изгиба, определяемый по таблицам Ф.1 - Ф.3 приложения Ф при ееf = 0 и
8.40 Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых элементов замкнутого и открытого сечений, подверженных сжатию с изгибом и внецентренному сжатию в двух плоскостях, следует выполнять по формуле
где ey, ex - действительные эксцентриситеты по направлению осей у и х при внецентренном сжатии и расчетные эксцентриситеты при сжатии с изгибом; yc, хc - координаты наиболее.сжатой точки сечения от совместного действия Мх, Мy и N; φc - коэффициент продольного изгиба, определяемый по таблицам Ф.1 - Ф.3 приложения Ф при ееf = 0 и
Кроме того, должен быть выполнен расчет по формуле (8.35) в предположении плоской формы потери устойчивости в плоскости оси у с эксцентриситетом еу (при еx = 0) и в плоскости оси х с эксцентриситетом ех (при еу = 0). 8.41 Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых балок, изгибаемых в одной плоскости, следует выполнять по формуле
где М - наибольший расчетный изгибающий момент в пределах расчетной длины lef сжатого пояса балки; Wc - момент сопротивления сечения балки для крайнего волокна сжатого пояса; ε - коэффициент, определяемый по формулам:
здесь æ - коэффициент, определяемый по формулам (8.6) и (8.7); φ b - коэффициент продольного изгиба, определяемый по таблицам Ф.1 - Ф.3 приложения Ф при eef = 0 и гибкости из плоскости стенки
8.42 Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых балок, изгибаемых в двух плоскостях, следует выполнять по формуле (8.50), при этом коэффициент φ b, следует принимать по таблицам Ф.1 - Ф.3 приложения Ф при eef = η erel. Здесь η - коэффициент, принимаемый по приложению Ф; erel - относительный эксцентриситет, определяемый по формуле
где σ fh - наибольшее напряжение в точке на боковой кромке сжатого пояса от изгибающего момента в горизонтальной плоскости в сечении, находящемся в пределах средней трети незакрепленной длины сжатого пояса балки; σ fv - напряжение в сжатом поясе балки от вертикальной нагрузки в том же сечении. 8.43 Проверка общей устойчивости разрезной балки и сжатой зоны пояса неразрезной балки не выполняется в случае, если сжатый пояс объединен с железобетонной или стальной плитой.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.011 с.) |



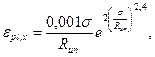
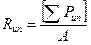 - нормативное сопротивление каната;
- нормативное сопротивление каната;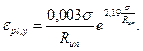
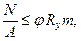
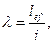
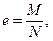
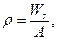
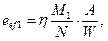


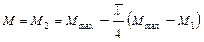
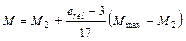
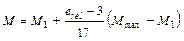
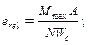
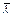 - условная гибкость; определяемая по формуле
- условная гибкость; определяемая по формуле 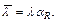 где α R - коэффициент, принимаемый по таблице Ф.4 приложения Ф.
Примечание - Во всех случаях следует принимать М ≥ 0,5 М max.
где α R - коэффициент, принимаемый по таблице Ф.4 приложения Ф.
Примечание - Во всех случаях следует принимать М ≥ 0,5 М max.