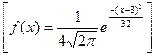Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительные интервалы для параметров нормального распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Надежность. Доверительные интервалы. Пусть
Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало. Если же о распределении имеется какая-либо информация, то можно сделать больше. Здесь речь будет идти об оценке параметров а к о случайной величины, имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим. Пусть Число γ=P{Θn-δ<Θ>Θn+δ}=P{|Θn-Θ|<δ} Заметим, что после того, как по данным выборки вычислена оценка Θn, событие {|Θn-Θ|<δ}становится или достоверным, или невозможным, так как интервал ( выборок объема n и для каждой из них построим интервал (
Определение. Доверительным интервалом называется найденный по данным выборки интервал ( Надежность у обычно принимают равной 0,95 или 0,99, или 0,999. Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр Θ. Но в этом можно быть уверенным на 95% при γ =0,95, на 99% при γ =0,99 и т.д. Это значит, что если сделать много выборок, то для 95% из них (если, например, γ =0,95) вычисленные доверительные интервалы действительно покроют Θ. 2. Доверительный интервал для математического ожидания при известном σ. В некоторых случаях среднее квадратичное отклонение а ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения осуществляются одним и тем же прибором при одних и тех же условиях. Итак, пусть случайная величина X распределена нормально с параметрами а и σ, причем σ известно. Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью γ. Данные выборки есть реализации случайных величин Х1, Х2,..., Хn, имеющих нормальное распределение с параметрами а и σ (§ 4.2, п. 1). Оказывается, что и выборочная средняя случайная величина X = 1/n(Х1 + Х2 +... + Хn) тоже имеет нормальное распределение (это мы примем без доказательства). При этом (см. § 4.2, пп. 2, 3) М(Х) = а; σ (Х) = σ/√n Потребуем, чтобы выполнялось соотношение Р(| X - а | < δ) = γ, где γ — заданная надежность. Пользуясь формулой (2.27) (§ 2.7, п. 2), получим Р(| X - а | < δ) =2Ф(σ/√n/σ), или Р(| X - а | < δ) =2Ф(t), где t = σ/√n/σ (4.15) Найдя из равенства (4.15) δ = t σ/√n, можем написать Р(| X - а | < t σ/√n) =2Ф(t), Так как Р задана и равна у, то окончательно имеем (для получения рабочей формулы выборочную среднюю заменяем на xB): P=(xB- t σ/√n<a<xB+ t σ/√n)=2Ф(t)= γ Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал (xB- t σ/√n;xB+ t σ/√n) покрывает неизвестный параметр а; точность оценки δ = t σ/√n. Здесь число tопределяется из равенства Ф(t) = γ/2 [оно следует из 2Ф(t)= γ] по таблице приложения 3. Как уже упоминалось, надежность у обычно принимают равной или 0,95 или 0,99, или 0,999. Пример. Признак X распределен в генеральной совокупности нормально с известным σ = 0,40. Найдем по данным выборки доверительный интервал для а с надежностью γ = 0,99, если n = 20, xB = 6,34.
Для Ф(t) = γ/2 = 0,99/2 = 0,495 находим по таблице приложения 3 t=2,58. Следовательно, δ = 2,58*0,40/√20= 0,23. Границы доверительного интервала 6,34-0,23 = 6,11 и 6,34 + 0,23 = 6,57. Итак, доверительный интервал (6,11; 6,57) покрывает а с надежностью 0,99. 3. Доверительный интервал для математического ожидания при неизвестном σ. Пусть случайная величина X имеет нормальное распределение с неизвестными нам параметрами а и σ. Оказывается, что случайная величина (ее возможные значения будем обозначать через t) Т = X-a/S/√n где n —объем выборки; X — выборочная средняя; S—исправленное среднее квадратичное отклонение, имеет распределение, не зависящее от a и σ. Оно называется распределением Стьюдента*. Плотность вероятности распределения Стьюдента дается формулой S(t,n)=Вn(1+t2/n-1)-n/2 где коэффициент Вn зависит от объема выборки. * Стьюдент — псевдоним английского статистика И. О. Госсета. Потребуем, чтобы выполнялось соотношение Р(|Т|<Tγ) = γ, где γ — заданная надежность. Так как S(t,n)— четная функция от t, то, пользуясь формулой (2.15) (см. § 2.5), получим P(|X-a|√n/S<tγ)=2∫ S(t,n)dt= γ Отсюда P=(X-tγS/√n<a< X+tγS/√n)= γ Следовательно, приходим к утверждению: с надежностью γ можно утверждать, что доверительный интервал (X-tγS/√n<a< X+tγS/√n) покрывает неизвестный параметр а, точность оценки t = tγS/√n. Здесь случайные величины X и S заменены неслучайными величинами х, и s, найденными по выборке. В приложении 4 приведена таблица значений tγ=t(γ, n) для различных значений γ и обычно задаваемых значений надежности. Заметим, что при n > 30 распределение Стьюдента практически не отличается от нормированного нормального распределения(см. § 2.7, п. 2). Это связано с тем, что lim(1+t2/n-1)-n/2=e-t2/2 Пример. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для хr с надежностью γ =0,99, если n = 20; ХB = б,34; s = 0,40. Для надежности γ =0,99 и n = 20 находим по таблице приложения 4 tγ = 2,861. Следовательно,δ = 2,861 • 0,40/√20=0,26. Концы доверительного интервала 6,34 - 0,26 = 6,08 и 6,34 + 0,26 = 6,60. Итак, доверительный интервал (6,08; 6,60) покрывает хr с надежностью 0,99. 4. Доверительный интервал для среднего квадратичного отклонения. Для нахождения доверительного интервала для среднего квадратичного отклонения а будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим (пп. 2 и 3). С надежностью γ можно утверждать, что доверительный интервал (s-sq; s+sq) покрывает неизвестный параметр σ; точность оценки δ = sq. В приложении 5 приведена таблица значений q=q(γ, n) для различных значений n и обычно задаваемых значений надежности γ. Пример 1. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для ог с надежностью γ =0,95, если n = 20; s=0,40. Для надежности γ =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40*0,37 = 0,15. Границы доверительного интервала 0,40-0,15= 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает σr с надежностью 0,95. Пример 2. На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратичное отклонение — 20 кг.
Определим: 1) доверительный интервал для математического ожидания а с надежностью 0,95; 2) доверительный интервал для среднего квадратичного отклонения с той же надежностью. При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности. Решение. 1) Согласно условиям задачи, хB = 340; s=20; γ= 0,95;n = 20. Пользуясь распределением Стьюдента, для надежности γ =0,95 и n = 20 находим в таблице приложения 4 tγ = 2,093. Следовательно,δ = 2,093*20/√20= 9,4. Границы доверительного интервала 340 - 9,4 = 330,6 и 340 + 9,4 = 349,4. Итак, доверительный интервал (330,6; 349,4) покрывает а с надежностью 0,95. Можно считать, что в данном случае истинная масса измерена достаточно точно (отклонение порядка 9,4/340= 0,03). 2) Для надежности γ =0,95 и n = 20 находим в таблице приложения 5 q=0,37. Далее, sq = 20- 0,37 = 7,4. Границы доверительного интервала 20 - 7,4 = 12,6 и 20 + 7,4 = 27,4. Таким образом, 12,6 < σ < 27,4, откуда можно заключить, что а определено неудовлетворительно (отклонение порядка sq/s = q = 0,4 — почти половина!). Чтобы сузить доверительный интервал при той же надежности, необходимо увеличить число проб n. Примечание. Выше предполагалось, что q<1. Если q>1, то, учитывая, что σ >0, получаем 0< σ <s+sq. Значения q и в этом случае определяются по таблице приложения 5. Пример 3. Признак X генеральной совокупности распределен нормально. По выборке объема n = 10 найдено «исправленное» среднее квадратичное отклонение s=0,16. Найдем доверительный интервал для σк с надежностью 0,999. Для надежности γ=0,999 и n= 10 по таблице приложения 5 находим q= 1,80. Следовательно, искомый доверительный интервал таков: 0 < σ < 0,16+ 0,16*1,80 или 0< σ < 0,448. 5. Оценка истинного значения измеряемой величины. Пусть проводится n независимых равноточных измерений* некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины Х1, Х2,..., Хn. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии σ2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются, следовательно, мы вправе использовать полученные в них предложения. Так как обычно а неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.
Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений хB = 42,319 и «исправленное» среднее квадратичное отклонение s = 5,0. Требуется оценить истинное значение а измеряемой величины с надежностью γ =0,99. Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала хB-tγs/√n<a< хB+tγs/√n покрывающего а с заданной надежностью γ =0,99. Пользуясь таблицей приложения 4 по γ =0,99 и n = 9, находим tγ=3,36. Найдем точность оценки: δ = tγs/√n = 3,36*5/√9 = 3,36*5/3 = 5,60. Границы доверительного интервала 42,319-5,60 = 36,719 и 42,319 + 5,60 = 47,919. Итак, с надежностью γ =0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719 < а< 47,919. То есть измерений, проводимых в одинаковых условиях. Эти условия считают выполненными, если измерения проводятся одним прибором.
Дополнительные упражнения К главе I 1. Найдите вероятность выпадения цифры при одном бросании монеты. [0.5] 2. Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков. [0,5] 3. В шар вписан куб. Точка ставится наугад в шар. Какова вероятность того, что она попадет в куб?
4. В книге 500 страниц. Чему равна вероятность того, что наугад открытая страница имеет порядковый номер, кратный 7? [0,142] 5. В урне 3 синих, 8 красных и 9 белых шаров. Какова вероятность появления: а) синего; б) красного; в) белого шара при одном вынимании шара из урны? [а) 0,15; б) 0,4; в) 0,45] 6. Студент из 30 экзаменационных билетов усвоил 24. Какова вероятность его успешного ответа на экзамене на билет при одном кратном извлечении билета? [0,8] 7. В сосуд вместимостью 10 л попала одна болезнетворная бактерия. Какова вероятность зачерпнуть ее при наборе из этого сосуда стакана воды (200 см3)? [0,02] 8. Отдел технического контроля обнаружил 3 бракованные книги в партии из случайно отобранных 100 книг. Найдите относительную частоту появления бракованных книг. [0,03] 9. По цели произведено 20 выстрелов, причем зарегистрировано 18 попадений. Найдите относительную частоту попаданий в цель. [0,9] 10.Среди 1000 новорожденных оказалось 517 мальчиков. Найдите относительную частоту рождения мальчиков. [0,517] 25. В День физкультурника Сизов пошел на стадион. Можно было купить билет на футбол с вероятностью 0,3 или купить билет на волейбол с вероятностью 0,2. Какова вероятность того, что Сизов попал на соревнования? [0,5] 25. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попасть в первую область равна 0,45; во вторую —0,35. Найдите вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область. [0,8] 25. Какова вероятность выпадения 4 или 6 очков при однократном бросании игральной кости?
25. В урне 2 синих, 6 красных и 12 белых шаров. Какова вероятность вынуть цветной шар, если вынимается один шар? [0,4] 25. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найдите вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков. [0,4] 25. В урне 4 белых и 3 синих шара. Каждое испытание состоит в том что наудачу извлекают один шар, не возвращая его обратно. Найдите вероятность появления синего шара при втором испытании, если при первом испытании был извлечен белый шар. [0,5] 25. В читальном зале имеется 6 учебников по теории вероятностей из которых 3 в переплете. Библиотекарь наудачу взял 2 учебника. Найдите вероятность того, что оба учебника окажутся в переплете. [0,2] 25. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобрали двух человек. Найдите вероятность того, что все отобранные лица окажутся мужчинами.
25. Студент знает 20 из 25 вопросов программы. Найдите вероятность того, что студент знает предложенные ему экзаменатором два вопроса.
25. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до10. Наудачу извлекают по одному 2 кубика. Найдите веростность того, что последовательно появятся кубики с номерами 1, 2, если кубики извлекаются без возвращения.
25. Для некоторой местности среднее число пасмурных дней в июле равно шести. Найдите вероятность того, что первого и второго июля будет ясная погода.
25. Среди 50 электрических лампочек три нестандартные. Найдите вероятность того, что две взятые подряд лампочки окажутся нестандартными.
22.Работница обслуживает два станка, работающие независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания работницы, для первого станка равна 0,9, для второго - 0,8. Найдите вероятность того, что в течение часа ни один из двух станков не потребует [0,72 23. Брошены две игральные кости. Какова вероятность того, что на обеих костях выпадут шестерки?
24.Экзаменационный билет содержит три вопроса. Вероятности того, что студент ответит на первый и второй вопросы билета, равны по 0,9, на третий —0,8. Найдите вероятность того, что студент сдаст экзамен, если для этого необходимо ответить на все вопросы. [0,648] 25. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найдите вероятность того, что пять первых покупателей потребуют обувь 41-го размера. [0,00032] 26. В семье трое детей. Принимая события, состоящие в рождении мальчика и девочки, равновероятными, найдите вероятность того, что в семье: а) все мальчики; б) дети одного пола. (а) [0,125]; б) [0,25] 27. В мешке смешаны нити, среди которых 30% белых, а остальные красные. Определите вероятность того, что вынутые наудачу две нити будут: а) белые; б) красные; в) одного цвета. [а) 0,09; б) 0,49; в) 0,58] 28. Пусть вероятность того, что человек умрет на 71-м году жизни, равна 0,04. Какова вероятность того, что из трех человек семидесяти лет через год все будут живы? [0,88] 29. Вероятность установления в данной местности устойчивого снежного покрова с октября равна 0,1. Определите вероятность того, что в ближайшие три года в этой местности устойчивый снежный покров с октября не установится ни разу. [0,729] 30. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике, соответственно равны 0,6; 0,7; 0,8. Найдите вероятность того, что формула содержится во всех трех справочниках. [0,336] 31. Брошены две игральные кости. Какова вероятность того, что хотя бы на одном, из кубиков выпадет 6 очков?
32. Производятся два выстрела по одной и той же мишени. Вероятность попадания при первом выстреле равна 0,6, для второго — 0,8. Найдите вероятность того, что в мишени будет хотя бы одна пробоина. [0,92] 33. В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% — с заболеванием L, 20%— с заболеванием М. Вероятность полного излечения болезни К равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Найдите вероятность того, что больной, поступивший в больницу, будет выписан здоровым. [0,77] 34. Для посева заготовлена смесь семян пшеницы 4 сортов. Зерен первого сорта 96%, второго— 1%, третьего —2% и четвертого сорта— 1%. Вероятности того, что из зерна каждого сорта вырастает колос, содержащий не менее 50 зерен, соответственно равны: 0,50; 0,15; 0,20; 0,05. Какова вероятность того, что колос, выросший из произвольно взятого из заготовленной смеси зерна, будет содержать не менее 50 зерен? [0,4995] 35. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника — 0,9, для велосипедиста — 0,8 и для бегуна — 0,75. Найдите вероятность того, что спортсмен, выбранный наудачу, выполнит норму. [0,86] 36. Партия электрических лампочек на 20% изготовлена первым заводом, на 30% — вторым и на 50% — третьим заводом. Для первого завода вероятность выпуска бракованной лампочки равна 0,01, для второго — 0,005 и для третьего — 0,006. Какова вероятность того, что наудачу взятая из партии лампочка окажется бракованной [0,0065] 37. Из 50 деталей 18 изготовлены в первом цехе, 20 — во втором, а остальные — в третьем. Первый и третий цехи изготавливают продукцию отличного качества с вероятностью 0,9, второй — с вероятностью 0,6. Какова вероятность того, что взятая наудачу деталь будет отличного качества? [0,78] 38. На четырех карточках написаны буквы А, Е, П, Р.Карточки перемешиваются и раскладываются в ряд. Какова вероятность того, что получится слово РЕПА?
40. В урне находятся 15 шаров, из них 9 красных и 6 синих. Найдите вероятность того, что вынутые наугад два шара оба окажутся красными.
41. Брошены две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 4.
42. В ящике имеется n шаров: m белых и n - m черных. Какова вероятность того, что среди r наудачу вынутых шаров окажется k белых?
К главе II 1. В лотерее на 100 билетов разыгрываются две вещи, стоимости которых 2100 и 600 р. Составьте закон распределения суммы выигрыша для лица, имеющего один билет.
2. Случайная величина задана законом распределения:
Какова вероятность, что она примет значение 4? [0,2] 3. Найдите математическое ожидание случайной величины Х, заданной законом распределения:
А)
Б)
В) [а) 6; б) 0,535; в) 5,3]
4. Найдите математическое ожидание случайной величины Z, если известны математические ожидания X и Y: a) Z=X+Y, M(X) = 5, M(Y) = 3; б) Z=3*+4y, M(X) = 2, M/(У) = 6. [а) 8; б) 30]
5. Производятся 3 выстрела с вероятностями попадания в цель, равными р1=0,4; р2=0,3 и р3=0,6. Найдите математическое ожидание общего числа попаданий. [1,3] 6. Независимые случайные величины X и Y заданы следующими законами распределения:
Найдите математическое ожидание случайной величины XY. [23,32] 7. Дискретная случайная величина Х принимает три возможных значения х1=4 с вероятностью р1=0,5; х2=6 с вероятностью р1=0,3 и х3 с вероятностью р3. Найдите х3 и р3, зная, что М(Х)=8. [х3=21, р3=0,2] 8. Дан перечень возможных значений дискретной случайной величины Х: х1=-1; х2=0; х3=1, а также известны математические ожидания этой величины и ее квадрата: М(Х)=0,1; [р1=0,4; р2=0,1; р3=0,5] 9. Найдите дисперсию случайной величины Х, заданной законом распределения:
А)
Б)
[а) D(X)=0,61; б) D(X)=1] 10. Определите математическое ожидание и дисперсию случайной величины Х, если закон распределения имеет вид:
[а) M(X)=2,6; б) D(X)=2,44] 11. Случайная величина Х распределена по закону:
Найдите М(Х), D(X), 12.Найдите D(X) и
[D(X)=15,21,
13. Известны дисперсии двух независимых случайных величин X и Y: D(X)=5, D(Y)=6. Найдите дисперсию суммы этих двух величин. [11] 14. Найдите дисперсии следующих величин: а) 2Х; б) -3Х, если D(X)=4. [а) 16 б) 36] 15. Дискретная случайная величина Х распределена по закону:
Найдите начальные моменты первого и второго порядков. [v1 = 3,9; v2=16,5]
16. Дискретная случайная величина X задана законом распределения:
Найдите центральный момент второго порядка.[m2=1,29] 17. Случайная величина X задана интегральной функцией: 0 при х<=-1 F(x)= 1 при х >1/3 Найдите вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0; 1/3) [0,25] 18. Случайная величина X на всей оси Ох задана интегральной функцией F(x)= [0,25] 19. Случайная величина X задана интегральной функцией 0 при х<=-2 F(x)= 1 при х >2 Найдите вероятность того, что в результате испытания величина X примет.значение, заключенное в интервале (-1; 1). [1/3] 20. Функция является плотностью вероятности случайной величины X. Найдите коэффициент а и функцию распределения F(x). [ 21. Случайная величина Х задана по всей оси Ох плотностью вероятности
Найдите постоянный параметр а. [a=1/2П]
22. Случайная величина X задана плотностью вероятности 0 при х<=- f(x)= 0 при х > Найдите коэффициент а. [a=1 ] 23. Случайная величина X задана плотностью вероятности f(x) = 2/3sin3x в интервале (0; П/3), вне этого интервала f(х) = 0. Найдите вероятность того, что X примет значение, принадлежащее интервалу (П/6;П/4) [ 24. Случайная величина X задана плотностью вероятности 0 при х <= 0; f(x) = 2х при 0 < х < =1; 0 при х > 1.
Найдите математическое ожидание случайной величины X [2/3] 25. Случайная величина X задана плотностью вероятности 0 при х <= -2; f(x) = 1/4 при -2 < х < =2; 0 при х > 2
Найдите математическое ожидание и дисперсию случайной величины X. [M(X)=0; D(X)=4/3] 26. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: одну партию из двух или две партии из четырех (ничьи во внимание не принимаются)? [Вероятнее выиграть одну партию из двух] 27. Пусть всхожесть семян данного растения составляет 70%. Определите вероятность того, что из трех посеянных семян взойдут: а) два; б) не менее двух.- [а) 0,441; б) 0,784] 28. В семье пятеро детей. Найдите вероятность того, что среди этих детей два мальчика. Вероятность рождения мальчика принять равной 0,51. [0,31] 29. Монету бросали четыре раза. Чему равна при этом вероятность выпадения герба два раза? [0,375]
30. Монета подбрасывается три раза. Какова вероятность того, что герб появится не менее двух раз? [0,5] 31. Монета подбрасывается три раза. Рассматривается случайная величина X— число появлений герба. Найдите закон распределения случайной величины X.
32. Найдите математическое ожидание числа бракованных изделий в партии из 10 000 изделий, если каждое изделие может оказаться бракованным с вероятностью 0,005. [50 изделий] 33. Из всей выпускаемой фабрикой продукции 98% составляют изделия со Знаком качества. Найдите: а) математическое ожидание и б) дисперсию числа изделий со Знаком качества в партии из 5000 изделий. [а) 4900; б) 98] 34. Подлежат исследованию 1200 проб руды. Пусть вероятность промышленного содержания металла в каждой пробе равна 0,09. Найдите: а) математическое ожидание и б) дисперсию числа проб с промышленным содержанием металла. [а) 108; б) 98,28] 35. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 3 и 2. Найдите плотность вероятности случайной величины X f(x). 36. Напишите дифференциальную функцию нормально распределенной случайной величины X, зная, что М(Х) = 3, D(X) = 16.
37. Нормально распределенная случайная величина X задана дифференциальной функцией Найдите математическое ожидание и дисперсию X. [М(Х) = 1, D(X) = 25] 38. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12; 14). [0,1359] 39. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найдите вероятность того, что в результате испытания X примет значение в интервале (15; 25). [0,6826] 40. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5 см, а среднее квадратическое отклонение равно 0,9 см. Найдите вероятность того, что отклонение диаметра наудачу взятой детали от математического ожидания по абсолютной величине будет меньше 2 см. [0,9736] 41. Проводится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением [0,383] 42. АТС получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно 2 вызова? [0,09] 43. Среди 1000 человек приблизительно 8 левшей. Какова вероятность того, что среди сотни наугад выбранных человек не окажется ни одного левши? [0,4493] 44. Монету подбрасывают 100 раз. Какова вероятность того, что при этом герб выпадет ровно 50 раз? [0,08] 45. Какова вероятность того, что при 200-кратном бросании монеты число случаев выпадения герба [0,5224] 46. Вероятность получения по лотерее проигрышного билета равна 0,1. Какова вероятность того, что среди 500 наугад купленных билетов не менее 48 и не более 55 безвыигрышных? [0,3913] 47. Какова вероятность того, что при подбрасывании монеты три раза герб выпадет по крайней мере один раз? [7/8] К главе III 1. Найдите законы распределения составляющих дискретной двумерной случайной величины, заданной законом распределения
2. Найдите вероятность того, что составляющая X двумерной случайной величины (X, Y) примет значение Х<2 и при этом составляющая Y примет значение Y< 4, если известна функция распределения величины (X, Y). F(x, у) = [0,849]
[1] Карл Гаусс(1777-1855)-немецкий математи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3919; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.019 с.) |

 — оцениваемый параметр,
— оцениваемый параметр, — его оценка, составленная из
— его оценка, составленная из  . Если известно, что оценка
. Если известно, что оценка  >0 некоторое число если неравенство выполняется
>0 некоторое число если неравенство выполняется  <
<  <
<  Большое значение для современной теории вероятностей имеют работы представителей советской школы, в частности А. Н. Колмогорова (1903-1987), С. Н. Бернштейна (1880-1968), А. Я. Хинчина (1894-1959), Ю. В. Линника (1915-1972) и Б. В. Гнеденко.
Большое значение для современной теории вероятностей имеют работы представителей советской школы, в частности А. Н. Колмогорова (1903-1987), С. Н. Бернштейна (1880-1968), А. Я. Хинчина (1894-1959), Ю. В. Линника (1915-1972) и Б. В. Гнеденко.
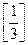











 . Найдите вероятности р1, р2, р3, соответсвующие возможным значениям х1, х2, х3.
. Найдите вероятности р1, р2, р3, соответсвующие возможным значениям х1, х2, х3. (X). [М(Х)=6, D(X)=9,
(X). [М(Х)=6, D(X)=9, 
 при -1 <х<= 1/3
при -1 <х<= 1/3
 . Найдите вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0; 1).
. Найдите вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0; 1). при -2 <х<= 2
при -2 <х<= 2
 ]
]
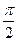
 при -
при -  ]
]