
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для математического ожиданияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть по выборке достаточно большого объема, n > 30, и при заданной доверительной вероятности 1– a необходимо определить доверительный интервал для математического ожидания mx, в качестве оценки которого используется среднее арифметическое
Закон распределения оценки математического ожидания близок к нормальному (распределение суммы независимых случайных величин с конечной дисперсией асимптотически нормально). Если потребовать абсолютную надежность оценки математического ожидания, то границы доверительного интервала будут бесконечными [– ∞, +∞]. Выбор любых более узких границ связан с риском ошибки, вероятность которой определяется уровнем значимости a. Интерес представляет максимальная точность оценки, т.е. наименьшее значение интервала. Для симметричных функций минимальный интервал тоже будет симметричным относительно оценки mx. В этом случае выражение для доверительной вероятности имеет вид P(| m*x – mx | < ε) = 1– a, где ε – абсолютная погрешность оценивания. Нормальный закон полностью определяется двумя параметрами – математическим ожиданием и дисперсией. Величина m*x является несмещенной, состоятельной и эффективной оценкой математического ожидания, поэтому ее значение принимаем за значение математического ожидания. Определим оценку дисперсии случайного параметра m*x, учитывая, что этот параметр равен среднему арифметическому одинаково распределенных случайных величин xi (следовательно, их дисперсии D(xi) одинаковы и равны S 2)
. Итак, случайная величина m*x распределена по нормальному закону с параметрами m*x и S2/n. Для установления необходимых соотношений целесообразно перейти к центрированным и нормированным величинам. Выражение m*x – mx можно трактовать как центрирование случайной величины m*x. Нормирование осуществляется делением на величину среднеквадратического отклонения оценки m*1
Для стандартизованной величины вероятность соблюдения неравенства определяется по функции нормального распределения
где u 21– a/2 = nε2/m*x. (3.1)
Нетрудно заметить, что это выражение аналогично по своему содержанию формуле, полученной с использованием общего метода построения доверительного интервала. При фиксированном объеме выборки из (3.1) следует, что чем больше доверительная вероятность 1– a, тем шире границы доверительного интервала (тем больше ошибка в оценке математического ожидания). Это равенство позволяет определить необходимый объем выборки для получения оценки математического ожидания с заданной надежностью и требуемой точностью (погрешностью): n=S2u21– a/2/ε 2. Если перейти к относительной погрешности ε0 = ε/ m*x, то n = S2 u21– a/2 /( ε0 2 m*x2). (3.2) Таким образом, чтобы снизить относительную погрешность на порядок, необходимо увеличить объем выборки на два порядка. Приведенная формула часто используется в статистическом моделировании для определения необходимого количества испытаний модели. Во многих случаях предположение о нормальном распределении случайной величины m*x становится приемлемым при n > 4 и вполне хорошо оправдывается при n >10. Оценка m*x вполне пригодна для применения вместо mх. Но не так обстоит дело с дисперсией, правомочность ее замены на S2 не обоснована даже в указанных случаях. При небольшом объеме выборки, n < 30, закон распределения оценки дисперсии S2 принимать за нормальный неоправданно. Ее распределение следует аппроксимировать распределением хи-квадрат как суммы квадратов центрированных величин (хи-квадрат распределение сходится к нормальному при количестве слагаемых, превышающем 30). Но это утверждение обосновано только для случая, когда случайная величина Х распределена нормально. С учетом сделанных допущений величина z будет подчиняться закону распределения Стьюдента с n –1 степенями свободы (одна степень свободы использована для определения оценки дисперсии). Распределение Стьюдента симметричное, поэтому полученное соотношение между точностью, надежностью оценки и объемом выборки сохраняется, меняются только значения квантилей. Вместо квантили нормального распределения u1– a/2 следует взять квантиль t1– a/2(n–1) распределения Стьюдента с (n –1) степенями свободы. Значения критических точек распределения Стьюдента для некоторых вероятностей и различных степеней свободы, представлены в таблицах. Сравнение таблиц показывает, что квантили распределения Стьюдента больше квантилей нормального распределения того же уровня надежности при малом n. Иначе говоря, применение нормального распределения при небольшом объеме выборки ЭД приводит к неоправданному завышению точности оценки. Пример 3.2. Определить с надежностью g = 0,9 доверительный интервал для математического ожидания случайной величины с точечными оценками m*х =27,51 и S2 =0,91, n = 44. Решение. Интервал двусторонний, симметричный a = 0,1. Объем выборки можно считать большим, поэтому воспользуемся нормальным распределением, тогда u0,95 = 1,96. Допустимое отклонение ε = u0,95(m*2 /n)0,5 =1,96 (0,91/44)0,5 = 0,28. С вероятностью 0,9 НДГ интервала составит θ 0 =27,51– 0,28=27,23, ВДГ интервала θ 1 = 27,51 + 0,28 = 27,79. Другими словами, с вероятностью 0,9 значение математического ожидания лежит в пределах от 27,23 до 27,79. Пример 3.3. Определить с надежностью g = 0,9 (a = 0,1) доверительный интервал для математического ожидания случайной величины с точечными оценками m*х = 55 и S2 = 658,6. Объем выборки n =6 Решение. Объем выборки n=6 нельзя считать большим, поэтому воспользуемся распределением Стьюдента при числе степеней свободы, равном 5. Тогда для двусторонней критической области в соответствии с табл. Функции Стьюдента допустимое отклонение стандартизованной случайной величины составит t0,9(4)=t(5; 0,1)= 2,015.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.167.85 (0.008 с.) |



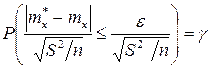
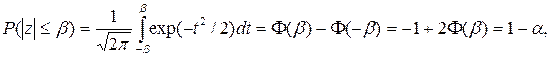
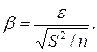 Значение β равно квантили u1–a/2 стандартного нормального распределения уровня 1– a /2. В частности, уровням надежности 0,9, 0,95 и 0,99 соответствуют значения допустимого отклонения u1– a/2 величины z, равные 1,64, 1,96 и 2,58 соответственно. Окончательно можно записать
Значение β равно квантили u1–a/2 стандартного нормального распределения уровня 1– a /2. В частности, уровням надежности 0,9, 0,95 и 0,99 соответствуют значения допустимого отклонения u1– a/2 величины z, равные 1,64, 1,96 и 2,58 соответственно. Окончательно можно записать


