
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события. Вероятность событияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА Формула полной вероятности является следствием основных правил теории вероятностей: теорем сложения и умножения вероятностей. Допустим, что проводится некоторый опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез): { H 1, H 2, ¼, Hn }, Hi Hj = при ij. (3.1) Каждая гипотеза осуществляется случайным образом и представляет собой некоторые события, вероятности которых известны:
Рассматривается некоторое событие A, которое может появиться только совместно с одной из гипотез (3.2). Заданы условные вероятности события A при каждой из гипотез:
Требуется найти вероятность события A. Для этого представим событие A как сумму n несовместных событий A = (A ÇH1)(A H2)... (A H n). (3.4) По правилу сложения вероятностей По правилу умножения вероятностей P(HiA)=P(Hi)P(A / Hi). Тогда полная вероятность события A:
т.е. полная вероятность события A вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе. Формула (3.5) называется формулой полной вероятности. Она применяется в тех случая, когда опыт со случайным исходом распадается на два этапа: на первом “разыгрываются” условия опята, а на втором – его результаты. Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса. По условиям опыта известно, что гипотезы
Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны
Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза
Вероятность наступления события A совместно с гипотезой Hk определяется с использованием теоремы умножения вероятностей: P(AHk)=P(Hk)P(A / Hk)=P(A)P(Hk / A). (3.6) Таким образом, можно записать: P (Hk / A) =P (Hk) P (A / Hk)/P (A). (3.7) С использованием формулы полной вероятности
Формула (3.8) называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А Пример 3.1. На вход радиоприемного устройства с вероятностью 0,9 поступает смесь полезного сигнала с помехой, а с вероятностью 0,1 только помеха. Если поступает полезный сигнал с помехой, то приемник с вероятностью 0,8 регистрирует наличие сигнала, если поступает только помеха, то регистрируется наличие сигнала с вероятностью 0,3. Известно, что приемник показал наличие сигнала. Какова вероятность того, что сигнал действительно пришел? Решение. С рассматриваемым событием A ={приемник зарегистрировал наличие сигнала} связано две гипотезы: H 1={пришел сигнал и помеха}, H 2={пришла только помеха}. Вероятности этих гипотез P(H 1)=0,9, P(H 2)=0,1. Условные вероятности события A по отношению к гипотезам H 1 и H 2находим из условия задачи: P(A / H 1)=0,8, P(A / H 2)=0,3. Требуется определить условную вероятность гипотезы H 1по отношению к событию A, для чего воспользуемся формулой Байеса:
Пример 3.2. Для решения вопроса идти в кино или на лекцию студент подбрасывает монету. Если студент пойдет на лекцию, он разберется в теме с вероятностью 0,9, а если в кино - с вероятностью 0,3. Какова вероятность того, что студент разберется в теме? Решение. Применим формулу полной вероятности (1.19). Пусть А - событие, состоящее в том, что студент разобрался в теме, событие (гипотеза) H1 - cтудент идет в кино, Н2 - студент идет на лекцию. Известны из условия задачи следующие вероятности: P(H1)=P(Н2)=0.5; P(A/Н1)=0,3; P(A/Н2)=0,9. Искомая вероятность события А будет равна P(A) = P(H1) P(A/ Н1)+ P(Н2) P(A/ Н2)=0,5 0,3+0,5 0,9=0,6.
Формула Бернулли Рассмотрим случай с двумя возможными исходами опытов, т.е. в результате каждого опыта событие A появляется с вероятностью р и не появляется с вероятностью q=1-p. Вероятность P(n,k) того, что в последовательности из n опытов интересующее нас событие произойдет ровно k раз (безразлично, в какой последовательности), равна (формула Бернулли)
Докажем это: Обозначим через Вк появление события А в k опытах и появление `А в (n – k) опытах. Событие Вк представляет собой сумму несовместимых событий Где Аi – появление события А в i-том опыте. Определим вероятность одного из вариантов серии испытаний. Так как все опыты одинаковы, то вероятности всех вариантов одинаковы равны Количество вариантов таких сложных событий равно числу выборок k номеров опытов из n возможных, в которых произойдут события А, т.е. равно Сnк. Тогда, согласно правилу сложения вероятностей для несовместных событий Р(Вк) равно
Следствия из формулы Бернулли. 1. Вероятность того, что событие А наступит менее k раз
2. Вероятность того, что событие наступит более k раз
3. Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз
4. Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой
Число к0, которому соответствует максимальная биномиальная вероятность Функция распределения Наиболее общей формой закона распределения, пригодной для всех случайных величин (как дискретных, так и недискретных) является функция распределения. Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x: F (x)=P{ X < x }.
1. 2. 3. F (x) – неубывающая функция своего аргумента, т.е. при x 1< x 2 F (x 1) £ F (x 2). Доказательство этого свойства иллюстрируется рис. 5.2. Представим событие C ={ X < x2 } как сумму двух несовместных событий С=A+B, где A ={ X < x1 } и B ={ x1£X<x2 }. По правилу сложения вероятностей P (C)= P (A)+ P (B), т.е. P { X < x2 }= P { X < x1 }+ P{ x1£X<x2 }, или F(x2)=F(x1)+P{ x1£X<x2 }. Но P{ x1£X<x2 }£0, следовательно, F (x 1) £ F (x 2) 4. P(α£ X < β) = F (β) - F (α), для "[α,β[ÎR. (5.4) Доказательство этого свойства вытекает из предыдущего доказательства. Вероятность того, что случайная величина Х в результате опыта попадет на участок от α до β (включая α) равна приращению функции распределени я на этом участке. Таким образом, функция распределения F(x)любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0≤F(x)≤1, причем F(-∞)=0, F(+∞)=1. Непрерывная случайная величина (НСВ). Плотность вероятности Случайная величина Х называется непрерывной, если ее функция распределения F(x) есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю P { X = α }=0 для любого α. В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности. Вероятность попадания непрерывной случайной величины X на участок от x до x +D x равна приращению функции распределения на этом участке: P{ x£ X < x +D x }= F (x +D x) - F (x). Плотность вероятности на этом участке определяется отношением
Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f (x). График плотности распределения называется кривой распределения. Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f (x) dx. Эта величина называется элементом вероятности. Вероятность попадания случайной величины X на произвольный участок [ a, b [ равна сумме элементарных вероятностей на этом участке:
В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f (x) и опирающейся на участок (α,β) (рис. 5.4).
В геометрической интерпретации F (x) равна площади, ограниченной сверху кривой плотности распределения f (x) и лежащей левее точки x (рис. 5.5). Основные свойства плотности распределения: 1. Плотность распределения неотрицательна: f (x) ³ 0. Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной. 2. Условие нормировки: Геометрически основные свойства плотности f(x) интерпретируются так: 1. вся кривая распределения лежит не ниже оси абсцисс; 2. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Математическое ожидание Математическое ожидание (МО) характеризует среднее взвешенное значение случайной величины. Для вычисления математического ожидания для ДСВ каждое значение xi учитывается с «весом», пропорциональным вероятности этого значения.
M[X]- оператор математического ожидания; mx -- число, полученное после вычислений по формуле. Для НСВ заменим отдельные значения
Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.
где сумма распространяется на все значения xi, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна. Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках. Моменты случайной величины Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Теми же приемами пользуются и в теории вероятностей. Чаще на практике применяются моменты двух видов: начальные и центральные. Начальный момент s -го порядка СВ X есть математическое ожидание s -й степени этой случайной величины: a s = M[ Xs ].
Математическое ожидание случайной величины является начальным моментом первого порядка Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:
Центрирование случайной величины аналогично переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию случайной величины. Центральным моментом s -го порядка СВ X есть математическое ожидание s -й степени центрированной случайной величины: m s = M[(X-mx) s ].
Очевидно, что для любой случайной величины Х центральный момент первого порядка равен нулю:
Приведем некоторые соотношения, связывающие начальные и центральные моменты: Для второго:
Для третьего центрального момента:
Аналогично можно получить моменты не только относительно начала координат (начальные моменты) или математического ожидания (центральные моменты), но и относительно произвольной точки а.
Дисперсия Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины. Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений. Расчетные формулы:
Дисперсия может быть вычислена через второй начальный момент:
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина. Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ. Средним квадратическим отклонением (СКО) СВ X называется характеристика
СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ. Свойства дисперсии Дисперсия постоянной величины с равна нулю. Доказательство: по определению дисперсии
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется. D[ X + c ] = D[ X ]. Доказательство: по определению дисперсии
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2. Доказательство: по определению дисперсии
Для среднего квадратичного отклонения это свойство имеет вид:
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М [ сХ ] больше, чем возможные значения Х вокруг М [ X ], т.е. Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале: [ m - 3 s; m + 3 s; ]. (6.15) Производящие функции В ряде случаев для определения важнейших числовых характеристик дискретных случайных величин может помочь аппарат производящих функций. Пусть имеется дискретная случайная величина X, принимающая неотрицательные целочисленные значения 0, 1, …, k, … с вероятностями p0, p1, …, pk, …; pk=P{X=k}. Производящей функцией случайной величины X называется функция вида:
где z – произвольный параметр(0<z≤1). Очевидно, что
Возьмем первую производную по z от производящей функции:
и полагаем в ней z =1:
т.е. математическому ожиданию случайной величины X. Таким образом, математическое ожидание неотрицательной целочисленной случайной величины равно первой производной ее производящей функции φ(z) при z=1. Возьмем вторую производную функции φ(z):
Полагая в ней z= 1, получим
Первая сумма является вторым начальным моментом α2 случайной величины X, а вторая – ее математическое ожидание. Тогда:
т.е. второй начальный момент случайной величины равен сумме второй производной от производящей функции при z=1 плюс ее математическое ожидание. Аналогично, берем третью производную:
и полагая в ней z= 1, получаем:
И так далее, что позволяет выразить начальные моменты более высокого порядка. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН Характеристические функции До сих пор мы задавали случайные величины законом распределения. Характеристическая функция - ещё один способ представления случайных величин. Пусть X - случайная величина. Её характеристической функцией w (t) назовём математическое ожидание случайной величины eitX: w(t)= MeitX, где под комплексной случайной величиной eitX мы понимаем комплексное число eit X =cos(tX) + i sin(tX), а M (eitX)= M [cos(tX)+ iM[ sin(tX)]; независимая переменная t имеет размерность X -1. Характеристическая функция - преобразование Фурье-Стилтьеса функции распределения:
В непрерывном случае w (t) - преобразование Фурье плотности вероятности:
Если w (t) абсолютно интегрируема, то обратное преобразование Фурье позволяет восстановить плотность f (x) по характеристической функции:
В дискретном случае:
Особо отметим дискретные случайные величины с целочисленными значениями, например, при xk = k:
здесь w (t) - ряд Фурье в комплексной форме, вероятности pk играют роль коэффициентов Фурье и легко восстанавливаются по f (t):
В общем случае восстановление закона распределения по характеристической функции тоже возможно, но более сложно.
Примеры применения характеристических функций 14.3.1.. Биноминальное распределение. Пусть дискретная случайная величина имеет биноминальное распределение X:B (n, p).
Дифференцирование даёт:
14.3.2. Пуассоновское распределение. Пусть дискретная случайная величина имеет пуассоновское распределение X:P(l).
Отсюда сразу найдём: M [ X ]=l, D[ X ]=l. 14.3.3. Экспоненциальный закон распределения. Пусть непрерывная случайная величина имеет экспоненциальное распределение X:Exp(m).
Из этого равенства следует:
14.4. Нормальный закон распределения. Пусть непрерывная случайная величина имеет нормальное распределение X:N(0, 1).
Примем во внимание, что eitx =cos(tx) + i sin(tx):
Второй из этих интегралов равен нулю, так как его подынтегральная функция нечётна. Ввиду чётности подынтегральной функции первого интеграла:
Обозначим:
Очевидно,
интегрируем по частям:
Таким образом, J’ (t)=- tJ (t), и J (0)= Решение этого дифференциального уравнения дает:
Окончательно: w (t)= Тогда для нормально распределенной случайной величины X:N(a, s): и сразу же находим: M[ X ]= a, D[ X ]=s2. По поводу характеристической функции нормального закона можно заметить интересное его свойство: сумма независимых нормально распределённых случайных величин распределена по нормальному закону. Действительно. Пусть X и Y независимые случайные величины, причём, X: N (a 1, s1), Y:N (a 2, s2), а Z = X + Y. Характеристические функции X и Y: wX (t)= Для характеристической функции Z имеем: wZ (t)= wX (t)× wY (t)=exp[ i (a 1+ a 2) t - но это означает, что Аналогичным свойством обладают и независимые пуассоновские случайные величины: сумма независимых случайных величин, распределённых по закону Пуассона, распределена по закону Пуассона. В самом деле, если X: P(l1), X: P(l2), то wX (t)=exp[l1(eit -1)], wY (t)=exp[l2(eit -1)], поэтому характеристическая функция случайной величины Z = X + Y: wZ (t)= wX (t)× wY (t)=exp[(l1+l2)(eit -1)], но это значит, что Z: P(l1+l2). Законы, сохраняющиеся при сложении независимых случайных величин, называются безгранично делимыми. Нормальный и пуассоновский - примеры таких законов.
ЗАКОН БОЛЬШИХ ЧИСЕЛ Пусть проводится опыт Е, в котором нас интересует признак Х, или СВ Х. При однократном проведении Е нельзя заранее сказать, какое значение примет Х. Но при n -кратном повторении «среднее» значение величины Х (среднее арифметическое) теряет случайный характер и становится близким к некоторой константе. Закон больших чисел – совокупность теорем, определяющих условия стремления средних арифметических значений случайных величин к некоторой константе, при увеличении числа опытов до бесконечности (n®¥).
НЕРАВЕНСТВА ЧЕБЫШЕВА Теорема. Для любой случайной величины X с mx, Dx выполняется следующее неравенство Доказательство: 1. Пусть величина Х – ДСВ. Изобразим значения Х и Мх в виде точек на числовой оси Ох
0 х1 А Мх В Вычислим вероятность того, что при некотором
Это событие заключается в том, что точка Х не попадет на отрезок [ mx-ε, mx+ε ], т.е.
для тех значений x, которые лежат вне отрезка [ mx-ε, mx+ε ]. Рассмотрим дисперсию с.в. Х:
Т.к. все слагаемые – положительные числа, то если убрать слагаемые, соответствующую отрезку [ mx-ε, mx+ε ], то можно записать:
т.к.
Þ 2. Для НСВ:
Применяя неравенство
Откуда и вытекает неравенство Чебышева для НСВ. Следствие. Доказательство: События ================================================================================== 1. Лемма: Пусть Х –СВ, e>0 – любое число. Тогда
Доказательство:
Т.к. Следствие. Д-во: Полагаем, вместо св Х – св Х-М(Х), т.к. М(Х-М(Х))2=D(X) и получаем неp-во. Следствие: (правило трех сигм для произвольного распределения): Полагаем в неравенстве Чебышева
Т.е. вероятность того, что отклонение св от ее МО выйдет за пределы трех СКО, не больше 1/9. Неравенствово Чебышева дает только верхнюю границ вероятности данного отклонения. Выше этой границы - значение не может быть ни при никаком распределении. СХОДИМОСТЬ ПО ВЕРОЯТНОСТИ
Последовательность случайных величин Xnсходится по вероятности к величине a,
где e,d - произвольно малые положительные числа. Одна из важнейших, но наиболее важных форм закона больших чисел – теорема Чебышева – она устанавливает связь между средним арифметическим наблюденных значений СВ и ее МО.
ТЕОРЕМА ЧЕБЫШЕВА Первая теорема Чебышева. При достаточно большом числе независимых опытов среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию:
Доказательство: Рассмотрим величину У равную
Определим числовые характеристики Yn my и DY.
Запишем неравенство Чебышева для величины Yn
Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство
Переходя к противоположному событию:
Т.е. вероятность может быть сколь угодно близкой к 1. Вторая теорема Чебышева: Если Х1.....Хn – последовательность попарно независимых СВ с МО mx1....mxn и дисперсиями Dx1..Dxn ограничены одним и тем же числом Dxi<L (i=1..n), L=const, тогда для любого e, d> 0 – бесконечно малых
Доказательство: Рассмотрим СВ
Применим к Y неравенство Чебышева:
Заменим:
Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство Т.е., взяв предел при n®¥ от обеих частей и
(так как вероятность не может быть больше 1).
Пример. Производится большое число n независимых опытов, в каждом из которых некоторая случайная величина имеет равномерное распределение на участке [1,2]. Рассматривается среднее арифметическое наблюденных значений случайной величины X. На основании Закона больших чисел выяснить, к какому числу а будет приближаться величина Y при n→∞. Оценить максимальную практически возможную ошибку равенства Y≈a. Решение.
Максимальное практически возможное значение ошибки ТЕОРЕМА БЕРНУЛЛИ
Пусть произведены n независимых опытов, в каждом из которых возможно событие А с вероятностью р. Тогда относительная частота появления события А в n опытах стремится по вероятности к вероятности появления А в одном опыте. Теорема Бернулли: При неограниченном увеличении числа опытов до n частота события А сходится по вероятности к его вероятности р: где
Событие Хi – число появлений события А в i-м опыте. СВ X может принимать только два значения: X=1 (событие наступило) и X=0 (событие не наступило). Пусть СВ Хi – индикатор события А в i-м опыте. Числовые характеристики хi: m i = p Di = pq. Они независимы, следовательно, можем применить теорему Чебышева:
Дробь
Пояснения: В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней. ВВЕДЕНИЕ Математической статистикой называется наука, занимающаяся методами обработки экспериментальных данных (ЭД), полученных в результате наблюдений над случайными явлениями. Перед любой наукой ставятся следующие задачи: Ø Описание явлений; Ø Анализ и прогноз; Ø Выборка оптимальных решений. Применительно к математической статистике пример задачи первого типа: пусть имеется статистический материал, представляющий собой случайные числа. Требуется его упростить, представить в виде таблиц и графиков, обеспечивающих наглядность и информа
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

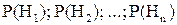 . (3.2)
. (3.2) (3.3)
(3.3) .
. , (3.5)
, (3.5) несовместны, образуют полную группу событий:
несовместны, образуют полную группу событий: Ø при
Ø при 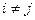 и
и  .
. ;
; 
 (послеопытные вероятности называются апостериорными):
(послеопытные вероятности называются апостериорными): .
. . (3.8)
. (3.8) .
. . (4.1)
. (4.1)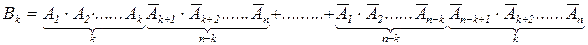

 =Cnкpкq(n-к).
=Cnкpкq(n-к).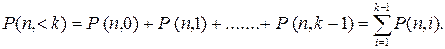 (4.2)
(4.2) (4.3)
(4.3) . (4.4)
. (4.4)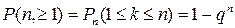 (4.5)
(4.5) , называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами:
, называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами:  . (4.6)
. (4.6) Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.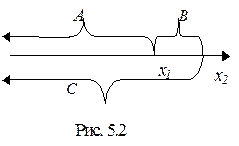
 F (-¥) = 0. (5.2)
F (-¥) = 0. (5.2) F (+¥) = 1. (5.3)
F (+¥) = 1. (5.3) (5.6)
(5.6) (5.7)
(5.7) Это соотношение позволяет выразить функцию распределения F (x) случайной величины X через ее плотность:
Это соотношение позволяет выразить функцию распределения F (x) случайной величины X через ее плотность: (5.8)
(5.8)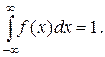 Это свойство следует из формулы (5.8), если положить в ней x =∞.
Это свойство следует из формулы (5.8), если положить в ней x =∞. (6.1)
(6.1) непрерывно изменяющимся параметром
непрерывно изменяющимся параметром  , соответствующие вероятности
, соответствующие вероятности  - элементом вероятности
- элементом вероятности 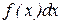 , а конечную сумму – интегралом:
, а конечную сумму – интегралом: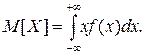 (6.2)
(6.2)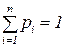 . Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью
. Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью 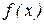 .
. , (6.3)
, (6.3)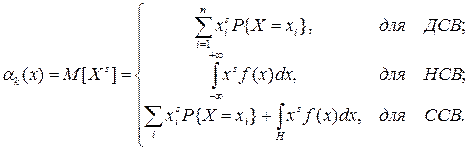 (6.7)
(6.7) .
. (6.8)
(6.8)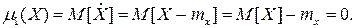

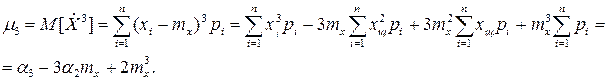
 (6.9)
(6.9) (6.10)
(6.10)
 . (6.11)
. (6.11)
 (6.12)
(6.12) . (6.13)
. (6.13)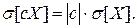 (6.14)
(6.14) . Если 0<½с½<1, то
. Если 0<½с½<1, то  .
.

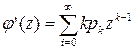
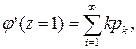
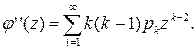
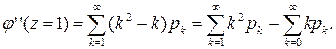
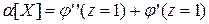 ,
,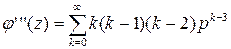
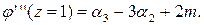
 .
.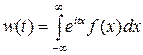
 .
. .
.
 .
. .
. .
. .
. .
.


 .
. .
. ;
;
 .
.
 .
.
 , wY (t)=
, wY (t)=  .
. t 2],
t 2],
 где e>0.
где e>0.
 величина Х отклонится от своего МО не меньше чем на ε:
величина Х отклонится от своего МО не меньше чем на ε: .
. --
-- .
. ,
, , то неравенство можно усилить
, то неравенство можно усилить
 Þ
Þ 

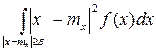 - это интегрирование по внешней части отрезка [ mx-ε, mx+ε ].
- это интегрирование по внешней части отрезка [ mx-ε, mx+ε ].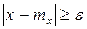 и подставляя его под знак интеграла, получаем
и подставляя его под знак интеграла, получаем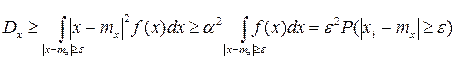 .
. - это 2-е неравенство Чебышева.
- это 2-е неравенство Чебышева. и
и  .
.
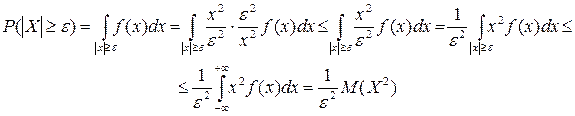 ,
, .
.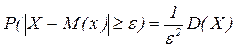 .
. , имеем
, имеем .
.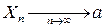 если при увеличении n вероятность того, что Xn и a будут сколь угодно близки, неограниченно приближается к единице:
если при увеличении n вероятность того, что Xn и a будут сколь угодно близки, неограниченно приближается к единице:

 .
.

 , где
, где  - сколь угодно малое число. Тогда
- сколь угодно малое число. Тогда .
.
 или
или 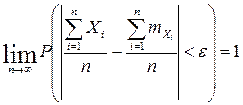
 .
. или
или 

 получаем:
получаем: .
.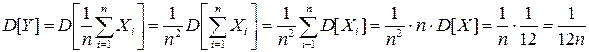 .
. .
.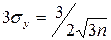 .
.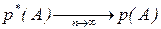 ,
, -- частота события А в n опытах, где m -число опытов в которых произошло событие А, n -число проведенных опытов или
-- частота события А в n опытах, где m -число опытов в которых произошло событие А, n -число проведенных опытов или или
или  .
.

 равна относительной частоте появлений события А в испытаниях Þ получаем
равна относительной частоте появлений события А в испытаниях Þ получаем .
.


