
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила сложения и умножения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Несколько событий называются несовместимыми, если появление одного из них исключает возможность появления остальных. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий P (AB) =P (A) +P (B). (2.1) Если имеется счетное множество несовместных событий A 1,..., An, то
Из правила сложения вероятностей вытекает, что если события A1, A2, …, An несовместны и образуют полную группу, то сумма их вероятностей равна единице; т.е. если
то
В частности, если два события А и
Тогда
Вероятность суммы двух совместных событий равна сумме вероятностей каждого из событий минус вероятность их совместного появления:
Вероятность суммы трех совместных событий
Событие A называется независимым от события B, если возможность наступления события A не зависит от того, произошло событие B или нет. В противном случае события являются зависимыми. Условной вероятностью события B при наличии A называется величина
(при этом полагается, что P(A) не равно 0). Условную вероятность события P(B/A) можно трактовать как вероятность события B, вычисленная при условии, что событие A произошло. На практике формулу (2.8) записывают в виде:
Вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого (правило умножения вероятностей). Правило умножения вероятностей может быть обобщено на случай произвольного числа событий
т.е. вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.
Событие A называется независимым от события B, если его вероятность не зависит от того, произошло событие B или нет, т.е. P(B / A)=P(B). Для независимых событий правило произведения вероятностей принимает вид:
Несколько событий A1, A2, …, An называются независимыми, если любое из них не зависит от любой комбинации (произведения) любого числа других. Для независимых событий правило умножения принимает вид:
или
т.е. вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий. Заметим, что если имеется несколько событий A1, A2, …, An, то их попарная независимость (т.е. независимость любых двух событий Ai и Aj, i≠j) еще не означает их независимости в совокупности.
Пример 2.1. Сообщение передается одновременно по n каналам связи, причем для надежности по каждому каналу оно повторяется k раз. При одной передаче сообщение (независимо от других) искажается с вероятностью p. Каждый канал связи (независимо от других) «забивается» помехами Решение. Обозначим события: A = {хотя бы один раз сообщение передано без искажений}; Bi = {по i -му каналу сообщение хотя бы один раз было передано без искажений}. Для выполнения события Вероятность того, что канал не «забит» помехами равна 1- q. Вероятность того, что хотя бы одно сообщение передано без помех – равна 1- pk (p – вероятность того, что все сообщения переданы с искажениями). Тогда P(B) = (1 - q) (1 - pk). Вероятность события A, состоящего в том, что хотя бы на одном канале произойдет событие, равна
Пример 1.5. Какова вероятность угадать в спортлото “5 из 36” не менее трех номеров? Решение. Событие А - угадать не менее трех номеров в спортлото, разбивается на сумму трех несовмеcтных событий: А3 - угадать ровно три номера; А4 - угадать ровно четыре номера; А5 - угадать ровно пять номеров. При этом P(A)=P(A3)+P(A4)+P(A5), так как события несовместны. Найдем вероятность P(A3). Для этого воспользуемся формулой (1.1). Здесь общее число комбинаций n по формуле (1.6) будет равно числу возможных заполнений карточек:
Число благоприятствующих комбинаций m в этом случае определяется следующим образом. Выбрать три номера из пяти выигравших можно Число таких выборок равно
Тогда
Аналогично вычисляются
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.177 (0.009 с.) |

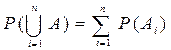 . (2.2)
. (2.2) AiּAj =О при i≠j,
AiּAj =О при i≠j,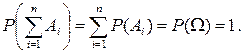 (2.3)
(2.3)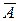 противоположны, то они образуют полную группу несовместных событий и
противоположны, то они образуют полную группу несовместных событий и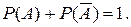 (2.4)
(2.4)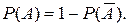 (2.5)
(2.5) . (2.6)
. (2.6)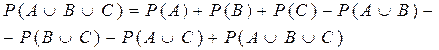 (2.7)
(2.7)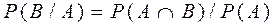 (2.8)
(2.8)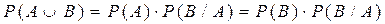 (2.9)
(2.9)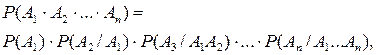 (2.10)
(2.10)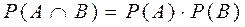 .(2.11)
.(2.11)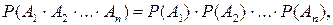 (2.12)
(2.12)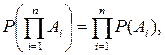 (2.13)
(2.13) с вероятностью q; «забитый» канал не может передавать сообщения. Найти вероятность того, что адресат получит сообщение без искажений.
с вероятностью q; «забитый» канал не может передавать сообщения. Найти вероятность того, что адресат получит сообщение без искажений.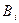
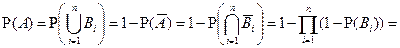
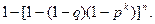
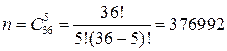 .
.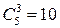 способами. Однако каждый выбор трех правильных номеров сочетается с выбором двух неправильных номеров.
способами. Однако каждый выбор трех правильных номеров сочетается с выбором двух неправильных номеров. . Таким образом, число благоприятствующих событий равно произведению найденных чисел:
. Таким образом, число благоприятствующих событий равно произведению найденных чисел: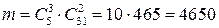 .
. .
.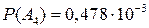 ,
, 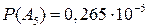 . Таким образом, искомая вероятность будет равна
. Таким образом, искомая вероятность будет равна .
.


