
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанная случайная величинаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случайная величина называется смешанной, если функция распределения F(x) на некоторых участках непрерывна, а в отдельных точках имеет разрывы (скачки). На тех участках, где F(x) непрерывна, вероятность каждого отдельного значения случайной величины равна нулю. Вероятность тех значений, где функция распределения совершает скачки, отличны от нуля и равны величине скачка.
Пример 5.1. По одной и той же стартовой позиции противника производится пуск из пяти ракет, причем вероятность попадания в цель при каждом пуске одной ракеты равна 0,8. Построить ряд распределения числа попаданий. Решение. Случайная величина X (число попаданий в цель) может принимать следующие значения: 0, 1, 2, 3, 4, 5. Найдем вероятность принятия величиной X этих значений, используя формулу Бернулли:
Ряд распределения имеет вид:
Пример 5.2. Случайная величина X распределена по закону, определяемому плотностью вероятности вида
Найти константу c, функцию распределения F (x) и вычислить P{| x | < /4}. Решение. Константу с вычислим исходя из условия нормировки:
откуда с = 0,5. Так как плотность вероятности задана различными формулами на разных интервалах, то и функцию распределения будем искать для каждого интервала в отдельности. Для x < -/2, для -/2 x /2 для x > /2,
Окончательно имеем
Вероятность P{| x | < /4}=
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Законы распределения случайной величины являются исчерпывающими характеристиками. Каждый закон распределения представляет собой некоторую функцию, указание которой полностью описывает случайную величину с вероятностной точки зрения. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями; зачастую достаточно бывает только отдельные числовые параметры, характеризующие отдельные черты распределения; например, среднее значение или разброс случайной величины («степень случайности»). Такие числа называются числовыми характеристиками случайной величины. Математическое ожидание Математическое ожидание (МО) характеризует среднее взвешенное значение случайной величины. Для вычисления математического ожидания для ДСВ каждое значение xi учитывается с «весом», пропорциональным вероятности этого значения.
M[X]- оператор математического ожидания; mx -- число, полученное после вычислений по формуле. Для НСВ заменим отдельные значения
Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.
где сумма распространяется на все значения xi, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна. Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках. Свойства математического ожидания. 1. Математическое ожидание неслучайной величины с равно самой величине с: M[ c ] = c. (6.4) Доказательствово: представим величину с как случайную величину, которая принимает одно и то же значение, с вероятностью р=1: M [ c ]= c ∙1= c. 2. При умножении СВ Х на неслучайную величину с не ту же самую величину увеличится ее математическое ожидание: M[ c × X ] = c×M[ X ]. (6.5) Доказательство:
3. При прибавлении к СВ Х неслучайной величины с к ее математическому ожиданию прибавляется такая же величина:
Доказательство: следует из свойств 1 и 3.
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: M [ X + Y ] = M [ X ]+ M [ Y ]. (6.6) Моменты случайной величины Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Теми же приемами пользуются и в теории вероятностей. Чаще на практике применяются моменты двух видов: начальные и центральные. Начальный момент s -го порядка СВ X есть математическое ожидание s -й степени этой случайной величины: a s = M[ Xs ].
Математическое ожидание случайной величины является начальным моментом первого порядка Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:
Центрирование случайной величины аналогично переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию случайной величины. Центральным моментом s -го порядка СВ X есть математическое ожидание s -й степени центрированной случайной величины: m s = M[(X-mx) s ].
Очевидно, что для любой случайной величины Х центральный момент первого порядка равен нулю:
Приведем некоторые соотношения, связывающие начальные и центральные моменты: Для второго:
Для третьего центрального момента:
Аналогично можно получить моменты не только относительно начала координат (начальные моменты) или математического ожидания (центральные моменты), но и относительно произвольной точки а.
Дисперсия Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины. Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений. Расчетные формулы:
Дисперсия может быть вычислена через второй начальный момент:
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина. Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ. Средним квадратическим отклонением (СКО) СВ X называется характеристика
СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ. Свойства дисперсии Дисперсия постоянной величины с равна нулю. Доказательство: по определению дисперсии
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется. D[ X + c ] = D[ X ]. Доказательство: по определению дисперсии
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2. Доказательство: по определению дисперсии
Для среднего квадратичного отклонения это свойство имеет вид:
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М [ сХ ] больше, чем возможные значения Х вокруг М [ X ], т.е. Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале: [ m - 3 s; m + 3 s; ]. (6.15)
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.163 (0.008 с.) |

 ,
, ,
, ,
, ,
, ,
, .
. .
. ,
,
 ,
, .
.
 .
. (6.1)
(6.1) непрерывно изменяющимся параметром
непрерывно изменяющимся параметром  , соответствующие вероятности
, соответствующие вероятности  - элементом вероятности
- элементом вероятности 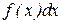 , а конечную сумму – интегралом:
, а конечную сумму – интегралом: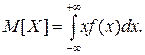 (6.2)
(6.2)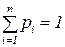 . Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью
. Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью 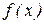 .
. , (6.3)
, (6.3)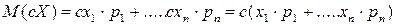
 (6.6)
(6.6)
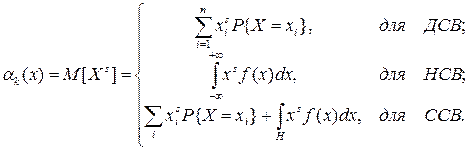 (6.7)
(6.7) .
. (6.8)
(6.8)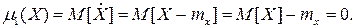

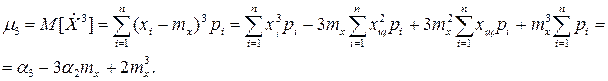
 (6.9)
(6.9) (6.10)
(6.10)
 . (6.11)
. (6.11)
 (6.12)
(6.12) . (6.13)
. (6.13)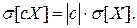 (6.14)
(6.14) . Если 0<½с½<1, то
. Если 0<½с½<1, то  .
.


