
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон распределения многомерной случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
N-мерной случайной величиной (Х1, Х2, …Хn) называется совокупность одномерных величин Хi , которые принимают значение в результате проведения одного и того же опыта. Это можно интерпретировать как случайные точки или случайные векторы в n -мерном пространстве. Например, совокупность n последовательных измерений с.в. Х - система n случайных величин. Полной характеристикой системы служит закон распределения, который может быть задан функцией распределения или плотностью вероятности. Функцией распределения n случайных величин (Х1, Х2...Хn) называется вероятность выполнения n неравенств вида Хi <xi: F(x1, x2...xn)=P((Х1 <x1)(Х2 <x2)... (Хn <xn)). Плотностью распределения системы n непрерывных с.в. называется n-я смешанная частная производная функции F(x1, x2...x n), взятая один раз по каждому аргументу:
Плотность распределения систем случайных величин обладает следующими свойствами: 1. 2.
Зная закон распределения системы, можно определить законы распределения отдельных величин, входящих в систему. Функция распределения каждой из величин, входящих в систему можно получить, если положить все остальные аргументы равными ¥: F1(x1)= F(x1, ¥......¥) или при выделении из системы случайных величин (Х1, Х2, …Хn) подсистемы случайных величин (Х1, Х2, …Хк) F1....к(x1)= F(x1......хк,¥......¥). Плотность распределения каждой из величин, входящих в систему, можно получить, интегрируя плотность распределения системы в бесконечных пределах по всем остальным аргументам:
Плотность распределения частной системы случайных величин (Х1, Х2, …Хn) подсистемы с.в. (Х1, Х2, …Хк) определяется так:
Условным законом распределения системы случайных величин (Х1, Х2, …Хn) называется ее закон распределения, вычисленный при условии, что остальные величины (Хк+1, Х к+2, …Хn) приняли значение (хк+1, х к+2, …хn). Условная плотность может быть вычислена по формуле: Случайные величины (Х1, Х2, …Хn) называются независимыми, если закон распределения каждой частной системы, выделенной из системы (Х1, Х2, …Хn), не зависит от того, какие значения приняли остальные случайные величины. Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему:
Вероятность попадания случайной точки (Х1, Х2, …Хn) в пределы n -мерной области D выражается n -кратным интегралом:
Эта формула является основной формулой для вычисления вероятностей событий, не сводящихся к схеме случаев. Переходят от схемы событий к схеме случайных величин (чаще всего – непрерывных) и сводят событие А к событию, состоящему в том, что система случайных величин (Х1, Х2, …Хn) окажется в пределах некоторой области D. Тогда вероятность события А может быть вычислена по этой формуле. 13.2. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН Как и в случае одномерных случайных величин, при невозможности точно установить законы распределения, применяют приближенное описание системы случайных величин с помощью минимального количества числовых характеристик. В качестве основных числовых характеристик используем следующие: 1. Вектор математических ожиданий M=(m1,m2,…mn) – характеризующих средние значения величин
2. Вектор дисперсий D =(D1,D2,…Dn) – характеризующих их рассеивание
3. Корреляционная матрица
где
характеризующих попарную корреляцию всех величин, входящих в систему. Дисперсия каждой из случайных величин
В случае, когда случайные величины не коррелированы, все элементы, кроме диагональной, равны 0 и корреляционная матрица принимает вид диагональной матрицы:
Помимо корреляционной матрицы для описания систем случайных величин может быть использована матрица коэффициентов корреляции. Это матрица, составленная не из корреляционных моментов, а из коэффициентов корреляции (нормированная корреляционная матрица):
где
Для некоррелированных случайных величин матрица коэффициентов корреляции вырождается в единичную матрицу:
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.01 с.) |

 .
.
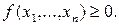



 .
.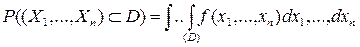

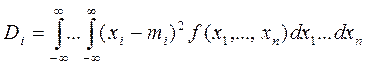
 ,
, или матрица коэффициентов корреляции
или матрица коэффициентов корреляции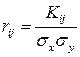 ,
, есть, по существу, не что иное, как корреляционный момент
есть, по существу, не что иное, как корреляционный момент 
 , поэтому корреляционная матрица и матрица коэффициентов корреляции принимает вид:
, поэтому корреляционная матрица и матрица коэффициентов корреляции принимает вид: ,
,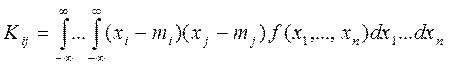

 ,
,
 .
.


