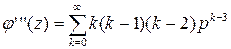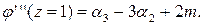Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнительные характеристики случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
6.4.1. Модой случайной величины называется ее наиболее вероятное значение, т.е. то значение, для которого вероятность pi (для дискретной СВ) или f (x) (для непрерывных СВ) достигают максимума. Обозначения: Mx, Mo.: Распределение с одним максимумом ряда распределения (для ДСВ) или плотности вероятности (НСВ) называется «унимодальным». Если многоугольник распределения или кривая распределения имеют несколько локальных максимумов, то такое распределение называют «полимодальным». Если распределение обладает не максимумом, а минимумом, то оно называется «антимодальным». 6.4.2. Медианой случайной величины X называется такое ее значение, для которого выполняется условие P{ X < Me } = P{ X ³ Me }. Медиана, как правило, существует только для непрерывных случайных величин:
Если известна функция распределения случайной величины Х, то Ме есть решение уравнения 6.4.3. Функция распределения Для решения обратной задачи используются следующие понятия. Квантилью c p случайной величины X является такое ее значение, для которого выполняется условие P{ X <c p } = F (c p) = p. Т.к. функция Очевидно, что квантиль, которая соответствует значению р=0.5, является медианой. Квантили
6.4.4.Третий центральный момент служит для характеристики асимметрии распределения. Если распределение симметрично относительно МО (масса распределена равномерно относительно центра тяжести), то все моменты нечетного порядка равны нулю. Поэтому для характеристик асимметрии выбирают третий центральный момент – он имеет размерность куба случайной величины. Безразмерный коэффициент асимметрии вычисляется так:
6.4.5. Четвертый центральный момент служит для характеристики так называемой «крутости», т.е. островершинности или плосковершинности распределения. Это свойство распределения описывается с помощью эксцесса:
6.4.6. Коэффициент вариации безразмерная величина, характеризует степень разбросанности значений СВ и вычисляется по формуле:
Пример 6.1. Из партии численностью 25 изделий, среди которых имеется шесть нестандартных, случайным образом выбраны три изделия. Найти математическое ожидание и среднее квадратическое отклонение нестандартных изделий, содержащихся в выборке. Решение. По условию задачи CB X принимает следующие значения: x 1=0; x 2=1; x 3=2; x 4=3. Вероятность того, что в этой выборке окажется ровно i (i = 0, 1, 2, 3) нестандартных изделий, вычисляется по формуле
откуда p 1=0,41; p 2=0,43; p 3=0,11; p 4=0,05. Дисперсию определим по формулам D[ X ] = M[ X 2] - (M[ X ])2, M[ X ] = 0 0,41 + 1 0,43 + 2 0,11 + 3 0,05 = 0,8, M[ X 2] = 0 0,41 + 1 0,43 + 22 0,11 + 32 0,05 = 1,32, D[ X ] = 1,32 - (0,8)2 = 0,68. Тогда
Пример 6.2. Непрерывная CB распределена по закону Лапласа:
Найти коэффициент b, математическое ожидание M[ X ], дисперсию D[ X ], среднее квадратическое отклонение [ X ]. Решение. Для нахождения коэффициента b воспользуемся свойством нормировки плотности распределения
Производящие функции В ряде случаев для определения важнейших числовых характеристик дискретных случайных величин может помочь аппарат производящих функций. Пусть имеется дискретная случайная величина X, принимающая неотрицательные целочисленные значения 0, 1, …, k, … с вероятностями p0, p1, …, pk, …; pk=P{X=k}. Производящей функцией случайной величины X называется функция вида:
где z – произвольный параметр(0<z≤1). Очевидно, что
Возьмем первую производную по z от производящей функции:
и полагаем в ней z =1:
т.е. математическому ожиданию случайной величины X. Таким образом, математическое ожидание неотрицательной целочисленной случайной величины равно первой производной ее производящей функции φ(z) при z=1. Возьмем вторую производную функции φ(z):
Полагая в ней z= 1, получим
Первая сумма является вторым начальным моментом α2 случайной величины X, а вторая – ее математическое ожидание. Тогда:
т.е. второй начальный момент случайной величины равен сумме второй производной от производящей функции при z=1 плюс ее математическое ожидание. Аналогично, берем третью производную:
и полагая в ней z= 1, получаем:
И так далее, что позволяет выразить начальные моменты более высокого порядка.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.198.181 (0.007 с.) |


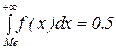

 случайной величины Х произвольному числу
случайной величины Х произвольному числу  ставит в соответствие вероятность.
ставит в соответствие вероятность.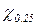 и
и  -называются нижней и верхней квантилью.
-называются нижней и верхней квантилью. (6.16)
(6.16) . (6.17)
. (6.17)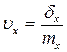 . (6.18)
. (6.18)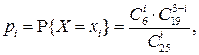
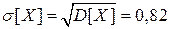 .
.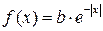 .
.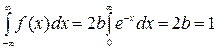 , откуда b = 1/2. Так как функция
, откуда b = 1/2. Так как функция 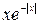 - нечетная, то
- нечетная, то 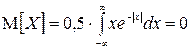 , дисперсия D[ X ] и СКО
, дисперсия D[ X ] и СКО  соответственно равны:
соответственно равны: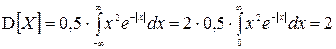 ,
,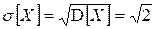 .
.

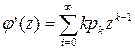
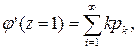
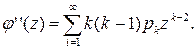
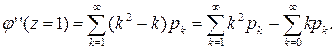
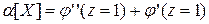 ,
,