
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики некоторых случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Числовые характеристики распределения вероятностей полезны тем, что помогают составить наглядное представление об этом распределении. Пусть Х1, Х2, …., Хn - взаимно независимые, одинаково распределенные случайные величины, а следовательно, одинаковы и их числовые характеристики. Обозначим среднее арифметическое этих величин через Тогда справедливы следующие предложения, устанавливающие связь между числовыми характеристиками среднего арифметического 1. Математическое ожидание среднего арифметического n одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию a каждой из величин, то есть М( 2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин D( Для среднего квадратического отклонения имеет место
Так как D и s служат мерами рассеяния случайной величины, то из (*) и (**) следует, что среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина. Более общими характеристиками случайных величин являются так называемые начальные и центральные теоретические моменты различных порядков. Начальным моментом порядка k случайной величины Х называют математическое ожидание величины Хk, то есть
В частности, при k = 1 получаем математическое ожидание
С помощью моментов первого и второго порядков можно получить следующую формулу для дисперсии
Центральным моментом порядка k случайной величины Х называют математическое ожидание отклонения степени k
В частности,
Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулу
Докажем, например, второе соотношение. По определению
Используя свойства математического ожидания и учитывая, что М(Х) есть постоянная величина, получим
Упражнения
1. Два консервных завода поставляют продукцию в магазин в пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90 %, а на втором – 80 %. В магазине куплено 3 банки консервов. Найти математическое ожидание M(X) и среднее квадратическое отклонение 2. Среди купленных семи билетов – три билета в партер. Наудачу взяли 4 билета. Составить закон распределения числа билетов в партер среди взятых. Найти функцию распределения этой случайной величины. 3. В коробке среди пяти деталей – две окрашенные. Детали извлекаются последовательно до появления обеих окрашенных деталей, после чего извлечения прекращаются. Составить закон распределения случайной величины Х – числа извлеченных деталей. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины. 4. Закон распределения случайной величины имеет вид Х 1 2 Р 0,3 0,7 Случайная величина Y биноминального распределения с параметрами n = 2, p = 0,4. Составить закон распределения случайной величины 5. Имеется пять ключей из которых два подходят к замку. Составить закон распределения числа Х проб при открывании замка, если использованный ключ в последующих пробах не участвует. Найти функцию распределения случайной величины Х, её математическое ожидание M(X) и дисперсию D(X). 6. При первичной поломке прибора, которая возможна с вероятностью 0,2, прибор ремонтируется. При вторичной поломке, происходящей с вероятностью 0,5, прибор снимается с испытаний. Составить закон распределения случайной величины Х – числа приборов, снятых с испытаний из трех проверяемых. Найти математическое ожидание и дисперсию этой случайной величины. 7. Полоса препятствий некоторых соревнований содержит три рубежа различной сложности. Спортсмен преодолевает эти рубежи без штрафных очков с вероятностями 0,8, 0,6, 0,4 соответственно. Составить закон распределения случайной величины Х – числа рубежей полосы препятствий, пройденных без штрафных очков. Найти математическое ожидание, дисперсию и функцию распределения этой величины. 8. Стрелок выстрелил три раза по удаляющейся мишени. Вероятность попадания в нее при первом выстреле равна 0,8, а с каждым следующим выстрелом она уменьшается на 0,1. Составить закон распределения случайной величины Х – числа попаданий в цель. Найти математическое ожидание и дисперсию этой случайной величины. 9. Лампочки елочной гирлянды соединены последовательно. Одна из них перегорела. Составить закон распределения числа проверенных лампочек до обнаружения перегоревшей, если в гирлянде 8 лампочек. Найти дисперсию этой случайной величины. 10. В ящике из 12 деталей – 8 окрашенных. Составить закон распределения случайной величины Х – числа окрашенных деталей среди четырех извлеченных, если после регистрации наличия (или отсутствия) окрашенности очередной извлеченной детали последняя возвращается назад в ящик. 11. Дискретная случайная величина Х принимает два значения: 12. Два товароведа проверяют партию изделий. Производительность их труда соотносится как 5:4. Вероятность определения брака первым товароведом составляет 85 %, вторым – 90 %. Из проверенных изделий отбирают четыре. Найти математическое ожидание и дисперсию числа готовых изделий среди отобранных. 13. В магазин поступили электролампы с трех заводов в пропорции 2:3:5. Доля брака в продукции первого завода – 5 %, второго – 2 %, третьего – 3 %. Покупатель приобрел 3 лампочки. Найти математическое ожидание и среднее квадратичное отклонение числа качественных лампочек среди купленных. 14. Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупатель, равна 0,6, а вероятность того, что второй – 0,8. Случайная величина Х – число покупок, сделанных покупателями. Найти функцию распределения случайной величины. 15. Партия содержит 20 телевизоров, среди которых шесть с дефектом. Купили два телевизора. Составить закон распределения исправных телевизоров. 16. Имеется 4 различных ключа, из которых только один подходит к замку. Составить закон распределения числа опробованных ключей, если опробованный ключ в дальнейшем не участвует в испытаниях. 17. Два баскетболиста по очереди забрасывают мяч в корзину с вероятностью попадания при каждом броске для первого 0,8, для второго – 0,7. Всего производится пять бросков. Составить закон распределения числа попаданий для каждого игрока, если начинает бросать первый баскетболист, а также закон распределения общего числа попаданий. 18. Вероятность того, что денежный автомат при опускании монеты сработает правильно, равна 0,97. Составить закон распределения числа опусканий монет в автомат до первого правильного срабатывания автомата. 19. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равном 0,7. Вычислить математическое ожидание и дисперсию этой случайной величины. 20. Составить закон распределения случайной величины, выражающей число попаданий в мишень при четырех выстрелах, если вероятность попадания при каждом выстреле равна 0,3. Вычислить её математическое ожидание и дисперсию, пользуясь только их определениями, а результаты проверить по формулам этих характеристик для случайной величины, распределенной по биноминальному закону. Закон больших чисел
Громадный опыт, накопленный человечеством за многовековую историю существования, дает основание принять в практической деятельности следующий принцип.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 .
. и соответствующими характеристиками каждой отдельной величины.
и соответствующими характеристиками каждой отдельной величины. ,
,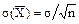 . (**)
. (**) . (7)
. (7) .
. .
. . (8)
. (8) ,
, .
. ,
, ,
, .
.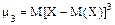 .
.

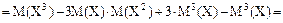
 .
. числа банок с продукцией высшего качества.
числа банок с продукцией высшего качества. , полагая, что X и Y – независимы. Проверить выполнение свойства дисперсии
, полагая, что X и Y – независимы. Проверить выполнение свойства дисперсии 
 , причём
, причём  . Известны:
. Известны:  . Найти закон распределения случайной величины Х.
. Найти закон распределения случайной величины Х.


