
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Технологий – ИМСИТ (г. Краснодар)Содержание книги
Поиск на нашем сайте Академия маркетинга и социально-информационных Технологий – ИМСИТ (г. Краснодар)
Кафедра общей и прикладной математики
Р.З. Камалян
Теория вероятностей И математическая статистика Учебное пособие для студентов экономических специальностей
Краснодар Кто так превратно рассуждает в области математики, от того, наверное, мало оснований ждать что-либо толкового и в других науках. Леонард Эйлер.
Предисловие
Настоящее пособие написано на основе лекций и семинарских занятий, проведенных автором в течение ряда лет в академии маркетинга и социально-информационных технологий. Пособие состоит из двух частей. В первой части изложены элементы теории вероятностей, иллюстрированные значительным числом решенных примеров. Вторая часть посвящена наиболее важным, с точки зрения прикладного применения, разделам математической статистики. Пособие содержит контрольные задания, предназначенные для самостоятельного выполнения студентами. Автор выражает глубокую благодарность президенту академии профессору С.Н Якаеву за поддержку и помощь при работе над рукописью настоящего пособия. Автор искренне признателен рецензентам - доктору физико- математических наук, профессору Кубанского государственного аграрного университета И.И. Ефремову и доктору технических наук, профессору Кубанского государственного технологического университета Г.Т. Вартумяну, чьи замечания и пожелания способствовали улучшению содержания пособия. Автор благодарит своих коллег, кандидатов физико- математических наук, доцентов А.И. Горшкова, И.В. Терещенко (КубГТУ), В.О. Осипяна, А.А. Халафяна (КубГУ) за содержательное обсуждение рукописи настоящего пособия, а также С.Р. Камаляна за помощь в подборе и решении значительного числа задач и упражнений. Введение Зарождение и первоначальное развитие теории вероятностей связано с решением задач статистики, с практикой страховых обществ и различных азартных игр. Последним принадлежит особая роль. Действительно, большинство первых задач теории вероятностей было связано с азартными играми. Азартные игры доставляли удобные схемы и модели, а отчасти и терминологию, позволявшие описать многие вероятностные явления и задачи. Конечно, и сами игры выдвигали задачи, стимулировавшие развитие теории вероятностей, хотя это и не было решающим. Следует отметить, что и сейчас при изложении начал теории вероятностей, в педагогических целях, преподаватели обращаются к играм в кости или в карты, так как в этих случаях легко подсчитать вероятности тех или иных возможных исходов. Занимаясь вопросами теории вероятностей, математики, естественно, встречаются и с вопросами комбинаторного характера. Например, Н. Тарталья определил число различных сочетаний из n элементов по m (без повторений), которое сейчас принято обозначать символом До середины XVII в. в теории вероятностей не было никакого общего метода решения задач, не говоря уже о цельной математической теории. Первым руководством по теории вероятностей была книга великого голландского ученого Христиана Гюйгенса. По поводу своего сочинения «О расчетах в азартной игре», Гюйгенс писал: «Я полагаю, что при внимательном изучении предмета читатель заметит, что имеет дело не только с игрой, но что здесь закладываются основы очень интересной и глубокой теории». Книга Гюйгенса выдержала ряд изданий и переводов и была фактически единственной по теории вероятностей до начала XVIII в. Она оказала большое влияние на многих ученых, в том числе и на Я. Бернулли. Теория вероятностей как наука возникла в середине XVII в., когда были выработаны её специфические понятия и методы. В этот же период появляются первые статистические работы так называемых политических арифметиков, видными представителями которых являются Джон Граунт и Вильям Петти. Конечно ни Д. Граунт, ни В. Петти в своих исследованиях не пользовались теорией вероятностей, но применявшиеся ими методы и понятия, по существу, были тесно связаны с теорией вероятностей, а поставленные в них вопросы стимулировали развитие этой науки. Необходимая связь между статистикой и теорией вероятностей была установлена только Я. Бернулли, с которого начался новый этап в истории теории вероятностей. Творчество Я. Бернулли в теории вероятностей было основополагающим. Его открытия в этой области изложены в книге «Искусство предположений», которое вышло в свет уже после его смерти, в 1713 году. В ней Я. Бернулли, прежде всего, высказывает общие соображения о природе случайных событий, а затем выводит носящую теперь его имя теорему, лежащую в основе всех последующих исследований о закономерностях случайных массовых явлений. Теорема Бернулли явилась первой и простейшей в цепи предложений, образующих закон больших чисел, - этот термин предложил в 1835 г. французский математик С. Пуассон. Вместе с теоремой Муавра-Лапласа и её обобщениями закон больших чисел принадлежит к числу предельных теорем теории вероятностей, принципиальное значение которых в том, что на них основаны все применения этой науки к природным и общественным явлениям. Первые исследования по теории вероятностей в России относятся к началу XIX в., когда по разным поводам Н.И. Лобачевскому, М.В. Остроградскому и В. Я. Буняковскому пришлось решить ряд частных задач. Формулировка и решение общих проблем теории вероятностей и начало становления её как большой математической науки со специфическими постановками проблем, играющих главную роль во всем естествознании, связаны с именами П.Л. Чебышева, А.М. Ляпунова и А.А. Маркова. Доказательством закона больших чисел П.Л. Чебышев не только открыл в науке общую и важную закономерность, но и дал исключительно простой и сильный метод важный как для теории вероятностей, так и для всей математики. На протяжении XIX в. и начала XX в. в России были созданы учебники по теории вероятностей, уровень которых соответствовал уровню развития теории вероятностей в нашей стране. Начало теоретико-вероятностных исследований в России связано с именами двух выдающихся математиков - А.Н. Колмогорова и А.Я. Хинчина. Фундаментальная монография А.Н. Колмогорова «Основные понятия теории вероятностей», а также книга, написанная им совместно с Б. Гнеденко, «Предельные распределения для сумм независимых случайных величин» были изданы на немецком, английском и др. языках. Вклад отечественных ученых в развитие теории вероятностей заслуживает самой высокой оценки. Создав аксиоматику теории вероятностей на базе теории меры и теории функций действительного переменного, они в корне изменили эту науку, заложили прочный логический фундамент для развития новых её ветвей. В последующем, благодаря развитию общих методов теории случайных процессов и полей открылись большие возможности для изучения собственно как явлений природы, так и экономических процессов.
Основные понятия и формулы теории Вероятностей
События
В любой науке есть основные понятия, на которые она опирается. Каждое последующее понятие определяется через предыдущие. Однако где-то этот процесс определения должен заканчиваться. Иными словами, должны быть первоначальные понятия, которые нельзя определить через другие; они лишь разъясняются, а все остальные сводятся к ним. Одним из таких понятий в теории вероятностей является понятие события. Под событием понимается всякий факт, который в результате эксперимента может произойти или не произойти. События обозначают заглавными буквами латинского алфавита: A, B, C и т.д. Два события называют несовместными, если появление одного из них исключает появление другого в одном и том же испытании. В противном случае события называются совместными. Элементы комбинаторики
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. Наиболее употребительны комбинации: перестановки, размещения и сочетания. Перестановками из n элементов называются соединения, каждое из которых содержит n элементов и которые отличаются между собой лишь порядком элементов. Число Рn всех перестановок из n элементов равно произведению последовательных натуральных чисел от 1 до n включительно, то есть Рn = 1 × 2 × 3… (n - 1)×n. (2) Произведение n натуральных чисел от 1 до n принято сокращенно обозначать n!, то есть Рn = 1 × 2 × 3 … (n - 1)n = n!; читается «n факториал» (от латинского factor - множитель). Тогда формулу (2) можно переписать в виде Рn = n! Пример: Р5 = 1 × 2 ×3× 4 ×5 = 120. Размещениями из n элементов по k (k £ n) называются соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются между собой элементами (хотя бы одним) или их порядком (k £ n). Число размещений из n элементов по k обозначается символом Число всевозможных размещений из n элементов по k равно произведению k последовательных чисел натурального ряда, наибольший из которых есть n, то есть
Например: Пользуясь понятием факториала, формулу (4) для числа размещений можно переписать так:
то есть
Сочетаниями из n элементов по k (k £ n) называются соединения, в каждое из которых входят k элементов, взятых из данных n элементов и которые отличаются только элементами (хотя бы одним) (k £ n). Число различных сочетаний из n элементов по k обозначается символом Вместо ( Число всевозможных сочетаний из n элементов по k равно частному от деления произведения последовательных чисел натурального ряда, наибольшее из которых равно n, на произведение последовательных натуральных чисел от 1 до k включительно, то есть
Формулу (6) можно выразить через число размещений и перестановок
или, учитывая (5),
Например:
Относительная частота
Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей. Относительной частотой (частостью) события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой W(A) = m/n, где m - число появлений события, n - общее число испытаний. Необходимо четко различать понятия вероятности и относительной частоты события. Вероятность события вычисляется до опытов и численно выражает меру объективной возможности наступления события, а относительная частота определяется лишь после того, как результаты опыта становятся известными. Пример. Монета подброшена пять раз. «Орел» выпал два раза. Каковы вероятность и частость выпадения «орла»? Решение. Вероятность выпадения «орла» есть р = 1/2 = 0,5 (из двух возможных исходов при подбрасывании монеты выпадению «орла» благоприятствует один), а частость выпадения «орла» есть 2/5 = 0,4 (событие наступило два раза в пяти испытаниях).
Для независимых событий Р(А + В) = Р(А) + Р(В) - Р(А) × Р(В). Для зависимых событий Р(А + В) = Р(А) + Р(В) - Р(А) × РА(В). Если события А и В несовместны, то Р(АВ) = 0 и (17) примет вид Р(А + В) = Р(А) + Р(В). Таким образом, формула (17) справедлива как для совместных, так и для несовместных событий.
Пример 2. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,75, вторым стрелком - 0,8, третьим стрелком - 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель. Решение. Р(А) = 0,75, Р(В) = 0,8, Р(С) = 0,9. Р(АВС) = Р(А) × Р(В) × Р(С) = 0,75 × 0,8 × 0,9 = 0,54. Пример 3. Вероятности появления каждого их трех независимых событий А1, А2, А3 соответственно равны р1, р2, р3. Найти вероятность появления только одного из этих событий. Решение. Заметим, что, например, появление только первого события А1 равносильно появлению события В1 - появилось только событие А1, то есть В1 = В2 - появилось только событие А2, то есть В2 = В3 - появилось только событие А3, то есть В3 = Таким образом, надо найти вероятность события В1 + В2 + В3, то есть вероятность появления одного, безразлично какого, из событий В1, В2, В3. Так как события В1, В2, В3 несовместны, то применима теорема сложения Р(В1 + В2 + В3) = Р(В1) + Р(В2) + Р(В3). (*)
Остается найти вероятности каждого из событий В1, В2, В3. События А1, А2, А3 независимы, следовательно, независимы события Р(В1) = Р ( Аналогично Р(В2) = Р(
Р(В3) = Р(
Подставив эти вероятности в (*), найдём искомую вероятность
Р(В1 + В2 + В3) = р1q1q3 + q1p2q3 + q1q2p3.
Пример 4. Вероятности попадания в цель при стрельбе из трех орудий таковы: р1 = 0,8, р2 = 0,7, р3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события А1 (попадание первого орудия), А2 (попадание второго орудия) и А3 (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям А1, А2 и А3 (то есть вероятности промахов), соответственно равны
q1 = 1 - p1 = 0,2, q2 = 1 - p2 = 0,3, q3 = 1 - p3 = 0,1.
Искомая вероятность Р(А) = 1 - q1q2q3 = 1 - 0,2 × 0,3 × 0,1 = 0,994.
Пример 5. Вероятность того, что событие появится хотя бы один раз в трех независимых в совокупности испытаниях, равна 0,936. Найти вероятность появления события в одном испытании, (вероятность появления события в одном испытании постоянна). Решение. Так как рассматриваемые события независимы в совокупности, то применима формула (16) Р(А) = 1 -
По условию, Р(А) = 0,936; n = 3. Следовательно,
0,936 = 1 - q3 или q3 = 1 - 0,936 = 0,064.
Отсюда q = Искомая вероятность p = 1 - q = 1 - 0,4 = 0,6. Упражнения Решить уравнения 1. 2.
Решить систему уравнений
3. Исходя из свойств сочетаний вычислить сумму
и проверить справедливость полученного равенства при n = 4. 4. В урне 4 белых и 6 черных шаров. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми. 5. В урне 8 белых и 6 красных шаров. Из урны вынимают сразу пять шаров. Найти вероятность того, что два из них будут белыми, а три красными. 6. В урне 6 белых, 8 синих и 5 красных шаров. Из урны вынимают один за другим все находящиеся в ней шары и записывают их цвета. Найти вероятность того, что в этом списке синий цвет появится раньше белого. 7. Имеются две урны: в первой 6 белых и 8 черных шаров; во второй 4 белых и 10 черных. Из каждой урны вынимается по шару. Найти вероятность того, что оба шара будут белыми; оба шара будут разных цветов. 8. В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны переложили во вторую наугад один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным. 9. В коробке 20 синих и 10 красных стержней. Из коробки вынимается один стержень, отмечается его цвет и стержень возвращается обратно в коробку. После этого из коробки извлекается один стержень. Найти вероятность того, что оба вынутые стержня будут синими. 10. В урне 4 белых и 6 черных шаров. Из урны вынимаются сразу два шара. Найти вероятность того, что эти шары будут разных цветов. 11. Пусть вероятность того, что в магазине сначала будет продана пара мужской обуви 44-го размера, равна 0,12, 45-го – 0,04, 46-го или большего – 0,01. Найти вероятность того, что сначала будет продана пара мужской обуви не менее 44-го размера. 12. В порт приходят корабли только из трех пунктов отправления. Вероятность появления корабля из первого пункта равна 0,2, из второго пункта – 0,6. Найти вероятность прибытия корабля из третьего пункта. 13. В партии содержатся 12 стандартных и 4 нестандартных деталей. Наудачу извлекаются 3 детали. Найти вероятность того, что среди извлеченных деталей: 1) не менее двух стандартных; 2) все три нестандартные; 3) хотя бы одна стандартная. 14. Имеются три урны. В первой урне 10 белых и 3 черных шара, во второй – 15 белых и 4 черных, и в третьей – 20 белых и 5 черных шаров. Из каждой урны наудачу извлекают по одному шару. Найти вероятность того, что: 1) только один шар оказался белым; 2) только два шара оказались белыми. 15. При массовом изготовлении изделий брак составляет в среднем 1,5 % общего количества всех изделий. Из числа готовых изделий 85,3 % составляют изделия первого сорта. Найти вероятность того, что наудачу взятое изделие окажется первого сорта. 16. Доказать, что произведение вероятностей противоположных событий не превышает 1/4. 17. В урне имеются два белых шара, два синих и три красных. Шары извлекаются наудачу по одному. Найти вероятность того, что белый шар появится раньше красного, если шар после извлечения в урну не возвращается. 18. Из партии изделий товаровед отбирает изделие высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,7. Найти вероятность того, что из трех наудачу взятых изделий, только два окажутся высшего сорта. 19. От аэровокзала отправились два автобуса к трапам самолета. Вероятность своевременного прибытия каждого автобуса равна 0,92. Найти вероятность событий: 1) оба автобуса прибудут вовремя; 2) оба автобуса опоздают; 3) только один автобус прибудет вовремя. 20. Имеется две партии деталей. Первая партия состоит из семи стандартных и трех нестандартных деталей, вторая – из десяти стандартных и четырех нестандартных. Из каждой партии наудачу извлекают по одной детали. Найти вероятности: 1) обе детали стандартные; 2) обе детали нестандартные; 3) одна стандартная и одна нестандартная. 21. В установку входят четыре одинаковые детали. Установка не будет работать, если при её сборке не менее трех деталей будут поставлены размера меньшего, чем необходимо. У сборщика осталось 15 деталей, среди которых 6 деталей меньшего размера. Сборщик берет детали наудачу. Найти вероятность того, что после сборки механизм будет работать. 22. Проверка партии риса, расфасованного по 1,0 кг дала следующие результаты: 20 % всех пачек были по 998 г, 60 % – по 1000 г, 20 % – по 1002 г. Из партии наудачу взяты две пачки. Найти вероятность того, что: 1) обе пачки имеют одинаковый вес; 2) общий вес этих пачек будет отклонен от нормы на 4 г. 23. В коробке содержится четыре новых одинаковых резца. Токарь, каждый раз приступая к работе, берет наудачу один из них, а после работы снова кладет в ту же коробку. Какова вероятность того, что за четыре смены в коробке не останется неиспользованных резцов, если в течение каждой смены токарь пользуется только одним резцом. 24. Изделие проверяется на стандартность. Вероятность того, что изделие стандартное, равна 0,95. Найти вероятность того, что из двух проверенных изделий только одно стандартное. 25. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность изготовления бракованной детали на первом станке равна 0,02, на втором – 0,03, на третьем – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего – в два раза меньше, чем второго. Взятая наугад деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем станке. 26. Пряжа поступает с трех станков, производительности которых относятся как 6:5:4. Вероятность того, что поступившая с первого станка пряжа будет высшего качества, равна 0,2, со второго – 0,3. Найти вероятность изготовления пряжи высшего качества на третьем станке, если среди продукции всех трех станков доля пряжи высшего качества равна 0,32. 27. При первом выстреле вероятность попадания первого стрелка равна – 0,8, второго – 0,9. При втором выстреле эта вероятность уменьшается на 0,2 для каждого стрелка. Найти вероятность того, что в мишени будет не менее двух пробоин, если каждый из стрелков сделал два выстрела. 28. В магазин поставляют изделия две фабрики. В продукции первой из них 90 % стандартных изделий, второй – 80 %. Известно, что во всей стандартной продукции магазина количество изделий фабрик относятся как 27:8. Изделие, отобранное случайным образом из всей продукции, оказалось нестандартным. Найти вероятность того, что оно изготовлено на второй фабрике. 29. Партия изготовленных деталей проверялась двумя контролерами. Первый контролер проверил 45 % деталей, второй – 55 %. Вероятность допустить ошибку при проверке для первого контролера 0,15, для второго 0,1. После проверки в партии деталей, признанных годными, обнаружена бракованная деталь. Какой из контролеров вероятнее допустил ошибку? 30. Имеется две партии одинаковых изделий. Первая партия состоит из 15 стандартных и 4 нестандартных, вторая – из 18 стандартных и 5 нестандартных. Из наудачу взятой партии наудачу извлечено одно изделие, которое оказалось стандартным. Найти вероятность того, что второе извлеченное изделие также окажется стандартным. 31. Имеется три партии одинаковых деталей. В первой 20 стандартных и 5 нестандартных, во второй – 15 стандартных и 3 нестандартных, в третьей – 14 стандартных и 2 нестандартных. Из наудачу взятой партии наудачу извлеченная деталь оказалась стандартной. Найти вероятность того, что эта деталь извлечена: 1) из первой партии; 2) из второй партии; 3) из третьей партии. Повторение испытаний Формула Бернулли
Важные закономерности теории вероятностей, имеющие применение в статистике, связываются с рассмотрением независимых повторных испытаний. Определение. Испытания называются независимыми по отношению к событию А, если вероятность появления события А в каждом испытании не зависит от исходов других испытаний. Под сложным событием принято понимать совмещение нескольких отдельных событий, называемых простыми. Пусть нужно решить такую задачу. Задача. Вероятность попадания в цель при одиночном выстреле равна р = 0,8. Производится четыре выстрела. Какова вероятность того, что цель будет поражена в точности три раза? Решение. Обозначим попадание в цель при отдельном выстреле через А, а промах - через Тогда возможны следующие сложные события: ААА Запись, например, ААА Интересующее нас событие В, что цель будет поражена ровно три раза, разлагается на следующие попарно несовместные события.
В = ААА
Число этих событий равно, очевидно, числу
Ввиду того, что испытания взаимно независимы (вероятность попасть в цель не зависит от того, были ли попадания или промахи при предыдущих выстрелах), можно применить формулу для вероятности совмещения независимых событий. Итак, Р(ААА = Аналогично Р(АА
Таким образом, вероятности событий, на которые разлагается В, одинаковы и равны
По теореме сложения
Р(В) = Р(ААА или Р(В) = Р(В) = 4×
Итак, вероятность появления события В в 4-х независимых испытаниях ровно три раза равна
р = 0,8, q = 0,2, Обозначим число независимых испытаний через n, число появлений события А в n испытаниях через k. Тогда, формула для определения вероятности того, что при n испытаниях событие А осуществится ровно k раз примет вид
Простейший поток событий Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени. Например, поток заявок, поступающих на предприятие бытового обслуживания; поток вызовов на станцию скорой помощи и т.д. Среднее число событий, происходящих в единицу времени, называется интенсивностью потока. Поток называется простейшим (пуассоновским), если он обладает следующими свойствами: 1) стационарности – вероятность наступления того или иного числа событий за некоторый промежуток времени t зависит только от длины этого промежутка и не зависит от начала его отсчета, т.е. интенсивность потока постоянна; 2) отсутствие последствия – вероятность наступления числа событий на любом промежутке не зависит от того, какое число событий наступило до начала этого промежутка 3) ординарности – вероятность появления двух и более событий за малый промежуток времени пренебрежимо мала по сравнению с вероятностью одного события. Рассмотрим подробнее перечисленные условия. 1. Условию стационарности удовлетворяет поток заявок, вероятностные характеристики которого не зависят от времени. В частности, для стационарного потока характерна постоянная плотность (среднее число заявок в единицу времени). На практике часто встречаются потоки заявок, которые (по крайней мере, на ограниченном отрезке времени) могут рассматриваться как стационарные. 2. Условие отсутствия последствия – наиболее существенное для простейшего потока – означает, что заявки поступают в систему независимо друг от друга. Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последствия потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не в другой момент, как правило, не связаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последствия может быть нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последствия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой 3. Условие ординарности означает, что заявки приходят поодиночке, а не парами, тройками и т.д. Например, поток клиентов, входящих в парикмахерскую, может считаться практически ординарным, чего нельзя сказать о потоке клиентов, направляющихся в ЗАГС для регистрации брака. Если поток событий является простейшим, то вероятность того, что за промежуток времени t некоторое событие А появится k раз, определяется формулой Пуассона
где λ – интенсивность потока. Эта формула отражает все три свойства простейшего потока, и поэтому является его математической моделью. Пример. Среднее число заявок, поступающих на комбинат бытового обслуживания за один час, равно четырем. Найти вероятность того, что за три часа поступит: 1) шесть заявок, 2) не менее шести заявок, 3) менее шести заявок. Решение. Пусть А – событие, означающее поступление одной заявки на комбинат бытового обслуживания. Так как интенсивность поступления заявок в единицу времени постоянна и число заявок, поступающих в любой промежуток времени, не зависит от того, сколько их поступило раньше, то поток является простейшим. Для решения задачи применима формула Пуассона, в которой λ = 4, t = 3, k = 6, 1. 2.
3. Упражнения
1. На каждые 30 штампованных изделий в среднем 6 изделий приходится с дефектом. Найти вероятность того, что из 5 наудачу взятых изделий 3 окажутся без дефекта. 2. Вероятность правильного оформления накладной при передаче продукции равна 0,8. Найти вероятность того, что из трех накладных только две оформлены правильно. 3. Играют 2 равносильных шахматиста. Что вероятнее выиграть: не менее трех партий из четырех или не менее пяти партий из 8. 4. Доля 3-го сорта некоторой массовой продукции в среднем составляет 20 %. Найти вероятность того, что из пяти наудачу взятых экземпляров этой продукции не менее трех окажутся 3-го сорта. 5. В партии, состоящей из изделий двух сортов, изделий 2-го сорта в полтора раза больше, чем 1-го сорта. Найти вероятность того, что среди трех наудачу взятых изделий окажется хотя бы одно 1-го сорта. 6. Вероятность выигрыша по одной облигации за весь срок займа равна 0,6. Куплено 5 облигаций. Найти вероятность того, что: 1) выигрыш выпадет на две облигации; 2) выигрыш выпадает хотя бы на одну облигацию; 3) выиграет не более двух облигаций. 7. Для обеспечения работы на некотором строительном объекте автопредприятие имеет 6 автомобилей. Вероятность выхода на линию в первую смену каждого из них равна 0,8. Найти вероятность нормальной работы автопредприятия, если в первую смену для этого на линии необходимо иметь не менее 4 автомобилей. 8. В партии содержится 12 стандартных и 4 нестандартных деталей. Наудачу извлекается 3 детали с возвращением. Найти вероятности того, что среди извлеченных деталей: 1) все три стандартные; 2) не более одной нестандартной; 3) хотя бы одна нестандартная. 9. На каждые 40 штампованных изделий, изготовленных станком-автоматом, приходится в среднем 4 дефектных. Из продукции станка наудачу взято 400 изделий. Найти вероятность того, что среди них 350 изделий окажутся без дефекта. 10. Завод отправил на базу 1000 доброкачественных изделий. За время пребывания в пути каждое изделие может быть повреждено с вероятностью 0,003. Найти вероятность того, что на базу прибудут 3 поврежденных изделия. 11. Всхожесть семян пшеницы составляет 95 %. Найти вероятность того, что из 2000 посеянных семян прорастут от 1880 до 1920. 12. Стандартных деталей автомат штампует в 5 раз больше, чем нестандартных. Наудачу отобрано 200 деталей. Найти вероятность того, что среди них 30 деталей нестандартных. 13. Найти вероятность остановки 20 станков из 80 работающих, если вероятность остановки каждого отдельного станка равна 0,3. 14. Посевной фонд содержит 92 % семян 1-го сорта. Наудачу взято 150 семян. Найти вероятность того, что среди этих семян содержится 140 семян 1-го сорта. 15. В банк поступило 5000 пачек денежных знаков. Вероятность того, что пачка неправильно укомплектована, т.е. содержит недостаточное или избыточное количество знаков, равна 0,0004. Найти вероятность того, что среди поступивших пачек не более одной пачки укомплектовано неправильно. 16. Устройство состоит из 2000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента равна 0,002. Найти вероятность отказа хотя бы одного элемента. 17. Вероятность того, что при сортировке стеклянное изделие будет разбито, равна 0,002. Найти вероятность того, что из 1500 изделий, прошедших сортировку, 4 изделия окажутся разбитыми. 18.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.015 с.) |


 . Важную роль в развитии комбинаторики сыграл «Трактат об арифметическом треугольнике» Б. Паскаля, который записал таблицу сочетаний в треугольной форме и который известен теперь как треугольник Паскаля.
. Важную роль в развитии комбинаторики сыграл «Трактат об арифметическом треугольнике» Б. Паскаля, который записал таблицу сочетаний в треугольной форме и который известен теперь как треугольник Паскаля. (от французского Arramgement - размещение).
(от французского Arramgement - размещение). = 8 · 7 · 6 · 5 · 4 = 6720.
= 8 · 7 · 6 · 5 · 4 = 6720.


 (5)
(5) (от латинского combinare - соединить).
(от латинского combinare - соединить). ).
). (6)
(6)
 (7)
(7)
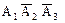 (появилось первое и не появились второе и третье события). Введем обозначения:
(появилось первое и не появились второе и третье события). Введем обозначения: ;
; ;
; .
.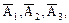 поэтому применима теорема умножения
поэтому применима теорема умножения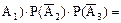 р1q2q3.
р1q2q3. q1p2q3;
q1p2q3;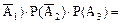 q1q2p3.
q1q2p3.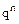 .
.
 .
. .
.


 (противоположное событие).
(противоположное событие). сочетаний из 4 по 3 (из четырех испытаний 1, 2, 3, 4 надо выбрать три, в которых выстрел окажется «удачным»; это можно сделать
сочетаний из 4 по 3 (из четырех испытаний 1, 2, 3, 4 надо выбрать три, в которых выстрел окажется «удачным»; это можно сделать  .
. .
. и т.д.
и т.д. +
+ 
 1 = 4 - 3.
1 = 4 - 3. . (1)
. (1) ,
, , k < 6.
, k < 6. ,
,
 ,
, .
.


