
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Можно доказать, что все свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Обобщением числовых характеристик, как и в случае дискретных величин, являются теоретические моменты различных порядков. Начальный теоретический момент порядка k непрерывной случайной величины Х определяется равенством
или
Центральный теоретический момент порядка k непрерывной случайной величины Х определяется равенством
или
Пример 1. Дана функция распределения непрерывной случайной величины Х
Найти числовые характеристики. Решение. Найдем плотность распределения
Найдем М(Х)
Дисперсию определим по формуле (7а)
Пример 2. Случайная величина Х задана плотностью распределения f(x) = 0,5x в интервале (0, 2); вне этого интервала f(x) = 0. Найти начальные и центральные моменты первого, второго и третьего порядков. Решение. По формуле
найдем начальные моменты
Найдем центральные моменты. Центральный момент первого порядка любой случайной (дискретной или непрерывной) величины равен нулю, то есть m1 = 0. Для нахождения центральных моментов второго и третьего порядков воспользуемся формулами, выражающими центральные моменты через начальные.
Упражнения 1. Случайная величина Х задана законом распределения
1. Найти параметр а; 2. Построить график распределения плотности f(x); 3. Найти вероятность попадания Х в промежуток (1; 2). 2. Дискретная случайная величина Х задана законом распределения
Найти F(x) и начертить график. 3. Случайная величина Х задана функцией распределения
Вычислить вероятность попадания случайной величины Х в интервалы (1,5; 2,5) и (2,5; 3,5). 4. Случайная величина Х задана плотностью распределения
1. Найти коэффициент а; 2. Построить график распределения f(x); 3. Найти вероятность попадания случайной величины Х в интервал (а/2; а). 5. Показать, что функция 6. В урне 5 белых и 25 черных шаров. Вынули 1 шар. Случайная величина Х – число вынутых белых шаров. Найти F(x). 7. Дана функция
Показать, что f(x) может служить плотностью вероятности некоторой случайной величины Х. Найти M(X), D(X) и σ(Х). 8. Дана функция
При каком значении λ функция f(x) может быть принята за плотность вероятностей случайной величины Х? Найти M(X), D(X) и σ(Х). 9. Дана плотность распределения непрерывной случайной величины
Определить а, моду и медиану. 10. Дана функция
При каком значении а функция f(x) является плотностью распределения случайной величины Х? Найти начальные и центральные моменты первых четырех порядков. Нарисовать график f(x). 11. Плотность распределения случайной величины имеет вид
Найти начальные и центральные моменты первых четырех порядков. Примеры непрерывных распределений
Равномерное распределение
Распределение вероятностей называют равномерным, если на промежутке, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. Найдем плотность равномерного распределения f(x), считая, что все возможные значения случайной величины заключены на промежутке [a, b], на котором функция f(x), сохраняет постоянные значения. По условию f(x) = 0 при x < a и x > b. Найдем постоянную С. Так как все возможные значения случайной величины принадлежат [a, b], то должно выполняться соотношение
Откуда
Таким образом
Функцию распределения найдем по формуле
Графики функций f(x) и F(x) представлены на рис. 9 и рис. 10.
Пример. Определить числовые характеристики M(X), D(X), s(X) случайной величины с равномерным распределением. Решение. Имеем
то есть Для нахождения дисперсии воспользуемся формулой
Нормальное распределение
Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические распределения подчинены закону нормального распределения, функция плотности вероятности которого имеет вид
Из (9) видно, что нормальное распределение определяется двумя параметрами: а и s, знание которых позволяет однозначно задать нормальное распределение. При произвольных значениях а и s (s > 0) нормальное распределение называют общим. Функция F(x) общего нормального распределения имеет вид
Если а = 0, s = 1, то нормальное распределение называют нормированным. Плотность нормированного распределения
Значения функции (10) табулированы (Приложение 1). Функция распределения имеет вид
которая также табулирована. Пример 1. Случайная величина Х распределена по нормальному закону. Найти математическое ожидание и среднее квадратическое отклонение этой величины. Решение. Для нахождения М(Х) воспользуемся формулой (4)
Заменим f(x) его выражением для нормального распределения (9), получим
Для нахождения несобственного интеграла осуществим замену переменной интегрирования по формуле
Первое слагаемое равно нулю. Действительно
Так как интеграл Пуассона
то второе слагаемое равно а. Итак,
Таким образом, математическое ожидание нормально распределенной случайной величины равно параметру а. Для нахождения дисперсии воспользуемся формулой (6). Учитывая, что
Заменим переменную интегрирования: z = (x – a)/s, x – a = sz, dx = sdz. Так как пределы интегрирования не меняются, получим
Интегрируя по частям, положив u = z,
Следовательно,
Итак, среднее квадратическое отклонение нормального распределения равно параметру s. Пример 2. Доказать, что
где Доказательство. Так как
то в силу симметрии j(х) относительно нуля имеем
а значит
С другой стороны
Тогда
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |


 .
.
 .
.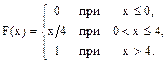
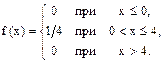
 .
. ,
, .
.
 ,
,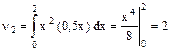 ,
, .
.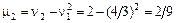 ,
,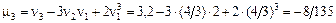 .
.


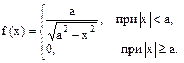
 является плотностью вероятности некоторой случайной величины Х, вычислить вероятность попадания случайной величины Х в интервал
является плотностью вероятности некоторой случайной величины Х, вычислить вероятность попадания случайной величины Х в интервал  .
.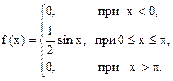
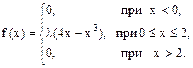

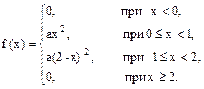

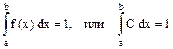 .
. .
.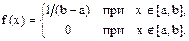
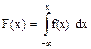 .
.

 ,
,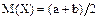 , как это и должно быть в силу симметрии распределения.
, как это и должно быть в силу симметрии распределения.

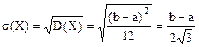 .
. . (9)
. (9) .
.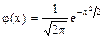 . (10)
. (10)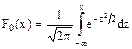 ,
, .
. .
. . Отсюда
. Отсюда  ,
, 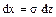 . Нетрудно установить, что пределы интегрирования не меняются, а значит
. Нетрудно установить, что пределы интегрирования не меняются, а значит .
.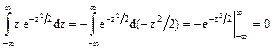 .
. ,
,
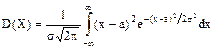 .
.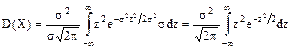 .
. , найдем
, найдем .
. .
. ,
,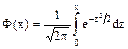 - функция Лапласа.
- функция Лапласа. ,
, ,
,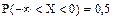 .
. .
.



