Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распределения непрерывных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю. Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:
Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения. Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины. Т. е. представить некоторую замену вероятностям Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения:
Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью f(x) на определенном участке оси абсцисс.
Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [ a; b ], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид:
Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами
Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении Нормальный закон распределения случайной величины Х с параметрами Согласно определению функция плотности вероятности и функция распределения связаны между собой:
Интеграл такого рода является "неберущимся", поэтому для его нахождения используют особую функцию, так называемый интеграл вероятностей или функцию Лапласа, для которой составлены таблицы (см. Приложение 2).
Используя функцию Лапласа можно выразить функцию распределения нормального закона по формуле:
Для практических целей очень важны свойства случайной величины, имеющей нормальный закон распределения.
Вычисление асимметрии и эксцесса позволяет установить симметричность распределения случайной величины
Центральный момент четвертого порядка используется для определения эксцесса, характеризует плосковершиннисть или гостровершиннисть плотности вероятности
Число 3 вычитается для сравнения отклонения от центрального закона распределения (нормального закона), для которого подтверждается равенство:
Итак,
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.007 с.) |

 .
. для дискретной случайной величины в непрерывном случае.
для дискретной случайной величины в непрерывном случае. .
.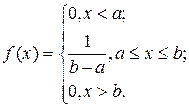


 и
и  (обозначают
(обозначают 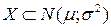 ), если ее плотность вероятности имеет вид:
), если ее плотность вероятности имеет вид: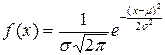 ,
где
,
где  ,
, 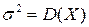 .
.


 и при
и при 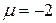 ). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при
). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при 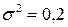 ;
;  ;
;  ). Таким образом, параметр
). Таким образом, параметр  (обозначается N (0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.
(обозначается N (0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.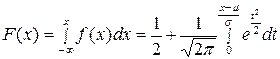 , где
, где  .
. ,
,
 - функция нечетная!
- функция нечетная!

 , где
, где 
 .
. (по абсолютной величине), равна:
(по абсолютной величине), равна: .
. ). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры (
). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры ( и
и  относительно
относительно  Для этого находят третий центральный момент, характеризующий асимметрию закона распределения случайной величины. Если он равен нулю
Для этого находят третий центральный момент, характеризующий асимметрию закона распределения случайной величины. Если он равен нулю  , то случайная величина
, то случайная величина  Поскольку
Поскольку  имеет размерность случайной величины в кубе, то вводят безразмерную величину — коэффициент асимметрии:
имеет размерность случайной величины в кубе, то вводят безразмерную величину — коэффициент асимметрии:
 Эксцесс вычисляется по формуле
Эксцесс вычисляется по формуле

 для нормального закона распределения. Если эксцесс положительный
для нормального закона распределения. Если эксцесс положительный  то на графике функция распределения остро вершину и для отрицательных значений
то на графике функция распределения остро вершину и для отрицательных значений 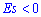 более пологую. Таким образом можно установить отклонения заданного закона от нормального. Для наглядности при различных значениях асимметрии и эксцесса
более пологую. Таким образом можно установить отклонения заданного закона от нормального. Для наглядности при различных значениях асимметрии и эксцесса  изображены на рисунках ниже
изображены на рисунках ниже