Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбинаторные задачи на перестановки.Содержание книги
Поиск на нашем сайте
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающихся только порядком расположения. Формула Общая постановка задачи: Каким количеством способов можно разместить N объектов на М мест. Особая разновидность задач на перестановки-объекты расположенные по кругу.
2 стул
3 стул Комбинаторная задача на вычисление числа сочетаний. Сочетаниями называют комбинации, составленные из n различных элементов по m элементов. которые отличаются хотя бы одним элементом. Формула Общая постановка задачи. Каким количеством способов можно выбрать М объектов из N? Ч К Б: Задача. Сколькими способами можно выбрать 5 деталей из ящик, содержащего10 деталей?
Комбинаторная задача на вычисление размещений. Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Формула Общая постановка задачи. Каким количеством способов можно разместить М объектов из N, учитывая порядок выбора(назначая объектам разные фун-ии) Перестановки- частный случай размещения, когда выбираются все объекты. Задача. Сколько можно составить сигналов из 6 флагов взятых по 2? ЗАМЕТИМ! Что числа размещений, сочетаний и перестановки связаны равенством:
Вопрос№ 7. Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных конфигураций (комбинаций), подчиненных тем или иным условиям, можно составить из заданных объектов. Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения. Правило суммы. Если некоторый объект A можно выбрать n способами, а другой объект B можно выбрать m способами, то выбор "либо A, либо B" можно осуществить n+m способами. Правило произведения. Если объект A можно выбрать n способами, а после каждого такого выбора другой объект B можно выбрать (независимо от выбора объекта А) m способами, то пары объектов A и B можно выбрать n*m способами. Вопрос №8. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Вопрос№9.
Бернулли: Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n с вероятностями, вычисляемыми по формуле Бернулли: где q=1-p; Биномиальный закон распределения. Случайная величина X принимает значения: 0, 1, 2, 3, 4, 5,..., п, с вероятностью, определяемой по формуле Бернулли
Вопрос№10. Геометрический закон распределения. Испытания проводятся до наступления события. Событие происходят с постоянной вероятностью. P=(const) P(A)=q^n-1*p
Вопрос№11.
ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Гипергеометрический закон определяется тремя параметрами N, М, п. При n<0, 1N этот закон стремится к биномиальному.
Вопрос№12. Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Теорема. Если вероятность р наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, произведение np = λ, то вероятность Рn(m) того, что в n независимых испытаниях события А наступит m раз, приближенно равна
Простейший поток событий Потоком событий называют последовательность событий, которые наступают в случайные потоки времени.
Простейшим(Пуассоновским) называют поток событий, обладает тремя свойствами: 1)стационарность, 2) отсутствие последствия, 3) ординарность. Сво-во стационарности. Вероятность появления k событий в любом промежуткевремени зависит только от числа k и от длительности промежутка времени и не зависит от начала отсчета. Свойство отсутствие последствия. Вероятность появления k событий не зависти от того появились или нет события в промежуток времени, предшествующее началу рассмотрения промежутка. Свойство ординарности Появление двух и более событий за малый промежуткок времени практически невозможно. Интенсивность потока λ называют сореднее число событий, которое появляется в еденицу времени. Если извеестна λ, то вероятность появления k событий простейшего потока за t определяется функцией
15.
16. Мат. ожидание дискретной случайной величины и его сво-ва
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.80.179 (0.009 с.) |

 =n!= n(n-1)(n-2)…
=n!= n(n-1)(n-2)…


 6 способов 1 стул 2 стул
6 способов 1 стул 2 стул
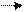 2 стул 3 стул
2 стул 3 стул
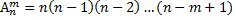

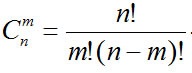 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.


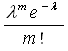 , т.е.
, т.е.