
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения вероятностей. Плотность вероятностейСодержание книги
Поиск на нашем сайте
Определение. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Для непрерывной случайной величины вводится понятие функции распределения. Определение. Функцией распределения вероятностей случайной величины Хназывают функцию F(х), определяющую для каждого значения x вероятность того, что случайная величина Х примет значение меньшее x, то есть F(х) = P(X < x)
Часто вместо термина «функция распределения» используют термин «интегральная функция распределения». Свойства функции распределения: 1. Значения функции распределения принадлежат отрезку [0; 1]: 0 ≤ F(х) ≤ 1. 2. Функция распределения есть неубывающая функция, то есть если x то F(x 3. Вероятность того, что случайная величина примет значение, заключенное в интервале [a; b), равна приращению функции распределения на этом интервале: P(a ≤ X < b) = F(b) – F(a). 4. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю: Р(Х = x 5. Если возможные значения случайной величины принадлежат интервалу (а; b), то F(x) = 0 при х ≤ a; F(х) = 1 при х ≥ b. 6. Если возможные значения непрерывной случайной величины расположены на всей оси Ox, то справедливы следующие предельные соотношения:
Определение. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x) = F'(x).
Часто вместо термина «плотность распределения вероятностей» используют термин «плотность вероятностей» и «дифференциальная функция». Свойства плотности распределения: 1. Плотность распределения неотрицательна в любой точке оси Ох: f(x)≥0 при х 2. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, b), определяется равенством: P(a < X < b) = 3. Зная плотность распределения, можно найти функцию распределения: F(x)= 4. Несобственный интеграл от плотности распределения в пределах от –∞ до +∞ равен единице:
5. Если все возможные значения случайной величины принадлежат интервалу (a; b), то
Определение. Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством М(Х)= где f(x) – плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (a; b), то М(Х)= Математическое ожидание обладает следующими свойствами: 1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С. 2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
3. Постоянный множитель можно выносить за знак математического ожидания:
4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
Определение. Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством: D(x)= Как и в случае с дискретной случайной величиной, можно показать, что D(x)= В частности, если все возможные значения Х принадлежат интервалу (a; b), то D(X)= или D(X)= Дисперсия обладает следующими свойствами: 1. Дисперсия постоянной равна нулю: D(C) =0. 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(CХ)=C 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:
4. Дисперсия произведения независимых случайных величин равна произведению дисперсий сомножителей:
5. Дисперсия суммы постоянной и независимой случайной величины равна квадрату постоянной на дисперсию независимой случайной величины:
Пример. Дана функция распределения непрерывной случайной величины Х
Требуется найти: 1. график F(x), 2. плотность f(x), 3. график f(x), 4. математическое ожидание М(Х), 5. дисперсию D(Х), 6. среднее квадратическое отклонение σ, 7. Р(Х < –2), P( Решение. 1. Построим график функции распределения
Рис. 2. График функции распределения. 2. Так как плотность f(x) равна первой производной от функции распределения f(x)= F′(х), то найдем производные от каждой из функций, составляющих функцию F(x):
Тогда получаем функцию f(x): f(x)= 3. Построим график плотности f(x)
Рис. 3. График плотности f(x).
Заметим, что при х=0 производная F′(х) не существует. 4. Найдем математическое ожидание непрерывной случайной величины Х: М(Х)=
5. Чтобы найти дисперсию непрерывной случайной величины Х, найдём математическое ожидание случайной величины Х М(Х Дисперсию найдем по формуле: D(Х) = M(Х 6. Среднее квадратическое отклонение σ найдем по формуле: σ(X) = 7. Найдем вероятность того, что случайная величина Х примет значение из интервала (– Р(Х< – 2) = F(– 2) = 0, Вторую вероятность Р( Р( Так как события Р
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.94.189 (0.012 с.) |

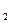 > x
> x 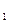 ,
, .
. (– ∞; +∞).
(– ∞; +∞). .
. .
. dx = 1.
dx = 1. = 1.
= 1. ,
, .
. .
. .
. .
.


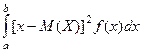
 .
. D(Х).
D(Х). .
. .
. .
.
 ≤ Х < 1) P(Х ≥
≤ Х < 1) P(Х ≥  ).
).
 .
.

 =
=  =
=  =
= 
 =
=  =
=  .
. =
=  =
= 
 =
= 
 =2.
=2. = 2 ─1,78 = 0,22.
= 2 ─1,78 = 0,22. =
=  = 0,47.
= 0,47. ;– 2), то есть Р(Х< – 2):
;– 2), то есть Р(Х< – 2): ≤ Х < 1) найдём по формуле Р(a ≤ Х < b)= F(b) – F(a):
≤ Х < 1) найдём по формуле Р(a ≤ Х < b)= F(b) – F(a): .
. и
и  противоположные, то вероятность события
противоположные, то вероятность события  находится по формуле:
находится по формуле: =1–
=1– 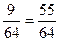 .
.


