
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное и нормальное распределенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Равномерное распределение Определение. Будем говорить, что распределение вероятностей непрерывной случайной величины является равномерным распределением, если плотность вероятности случайной величины Х имеет вид: f(x)= Найдем значение с. Так как плотность вероятности удовлетворяет условию:
то получаем:
Так как f(x)=c на промежутке [a;b], то Итак, равномерно распределённая случайная величина имеет плотность вероятности: f(x)= Пример. Если распределение случайной величины Х – равномерное и задан отрезок [2;8], то b – a = 8 – 2 = 6 и f(x)= Найдем числовые характеристики равномерного распределения. 1. Математическое ожидание равномерного распределения. М(Х)= Пример. Для предыдущей задачи найдем математическое ожидание М(Х)= 2. Дисперсия равномерного распределения. D(Х) =
=
Пример. Для предыдущей задачи найдем дисперсию: D(Х) = Нормальное распределение Определение. Случайная величина Х имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид: f(x)= где σ и a – параметры распределения. Определение. График функции f(x) называется нормальной кривой или кривой нормального распределения. Методами дифференциального исчисления можно установить, что: 1. кривая симметрична относительно прямой х= a; 2. функция имеет максимум при х= a f(a)= 3. по мере удаления х от точки a функция убывает и при х→ 4. кривая выпукла вверх при х є (a – σ; a + σ) и выпукла вниз при х є (– ∞; a – σ) и х є (a + σ; + ∞).

Рис. 4. Кривая нормального распределения. Замечание. Форма кривой изменяется с изменением параметра σ. С возрастанием σ кривая f(x) становится более пологой и растянутой вдоль оси Ох. Значениям случайной величины, близким к математическому ожиданию, соответствует большая плотность вероятности, то есть малые отклонения значений случайной величины от ее математического ожидания встречаются чаще, чем большие. Так как случайная величина определена на всей числовой оси, то при вычислении числовых характеристик рассматривается интеграл на промежутке (– ∞; +∞). Можно показать, что: М(Х) = D(Х)= σ(Х) = σ. Свойства нормального распределения. 1. Вероятность того, что нормально распределенная случайная величина Х примет значение, принадлежащее интервалу (α; β), находится по формуле: Р(α < Х < β) = Ф где Φ(х) 2. Вероятность того, что абсолютная величина отклонения меньше положительного числа δ находится по формуле: Р( В частности при a =0 справедливо равенство: Р( Правило «3 σ». Для нормально распределенной случайной величины велика вероятность того, что при однократном испытании отклонение величины от ее математического ожидания не превышает среднего квадратического отклонения. Преобразуем формулу Р( Р( Если t=3 и, следовательно, σ·t=3σ, то Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти, что значения нормально распределенной случайной величины выйдут за пределы интервала (a – 3σ; a + 3σ). Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможным. В этом и состоит сущность правила трех сигм.
Решение. Воспользуемся формулой: Р(α<Х<β)=Ф По условию, α = 19; β = 23; а = 11; σ = 4, тогда Р(19<Х<23)=Ф По таблице приложения 2 находим: Ф(3)=0,49865, Ф(2)=0,4772. Найдем искомую вероятность (вероятность того, что в результате испытания Х примет значение, заключенное в интервале (19;23)): Р(19<Х<23)=0,49865 – 0,4772=0,02145. Пример 2. Математическое ожидание нормально распределенной случайной величины Х равно 5 и среднее квадратическое отклонение равно 2. Написать плотность вероятности Х. Решение. Плотность нормально распределенрон случайной величины Х имеет вид: f(x)= Подставив a =5 и σ=2, получим: f(x)=
§13. Статистическое распределение выборки
Пусть для изучения количественного (дискретного или непрерывного) признака Х из генеральной совокупности извлечена выборка, причем значение x1 наблюдалось n1 раз, значение x2 наблюдалось n2 раз, …, значение xk наблюдалось nk раз. Наблюдаемые значения xi (i = 1, 2, …, n) признака Х называют вариантами, а последовательность всех вариант, записанных в возрастающем порядке, – вариационным рядом. Числа наблюдений ni называют частотами, их сумма Статистическим распределением выборки называют перечень вариант xi вариационного ряда и соответствующих им частот ni (сумма всех частот равна объему выборки n) или относительных частот Wi (сумма всех относительных частот равна единице). Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал). Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами (или относительными частотами). Пример. Задано распределение частот выборки объема n = 20:
В данной выборке получены следующие варианты x1 = 2; x2 = 6; x3 = 12, соответствующие частоты n1 = 3; n2 = 10; n3 = 7. Напишем распределение относительных частот. Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки
Напишем распределение относительных частот:
Контроль: сумма всех относительных частот
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2914; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 =1,
=1,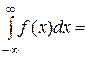
 .
.

 , следовательно, c =
, следовательно, c =  .
.

 =
= 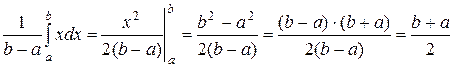 .
. .
. =
=
 .
. .
. ,
, ;
; ∞ кривая приближается к оси Ох;
∞ кривая приближается к оси Ох; 0 a X
0 a X
 =
=  ,
, ,
, —Ф
—Ф  ,
, – функция Лапласа (см. приложение 2).
– функция Лапласа (см. приложение 2). <δ)=2Ф(
<δ)=2Ф( ).
). <δ)= 2Ф(
<δ)= 2Ф( ).
). <
<  =
=  , то есть вероятность того, что отклонение от математического ожидания по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Это и есть правило «3 σ».
, то есть вероятность того, что отклонение от математического ожидания по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Это и есть правило «3 σ». Пример 1.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны соответственно 11 и 4. Найти вероятность того, что в результате испытания Х примет значение, заключенного в интервале (19;23).
Пример 1.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны соответственно 11 и 4. Найти вероятность того, что в результате испытания Х примет значение, заключенного в интервале (19;23). – Ф
– Ф  = Ф(3) – Ф(2).
= Ф(3) – Ф(2). .
. .
. ─ объем выборки. Отношения частот к объему выборки
─ объем выборки. Отношения частот к объему выборки  ─ относительными частотами.
─ относительными частотами.

 = 3 + 10 + 7 = 20.
= 3 + 10 + 7 = 20. ─ относительные частоты:
─ относительные частоты: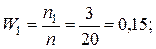



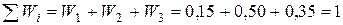 .
.


