
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трапецеидальные распределенияСодержание книги
Поиск на нашем сайте
К трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение (рис. 6.5,а) описывается уравнением
Трапецеидальное распределение (рис 6.5,6) образуется как композиция двух равномерных распределений шириной а, и а2.
Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона) Нормальное распределение (распределение Гаусса) Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гауссах При введении новой переменной t = (х-Хц)/а из (6.6) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49]. Определенный интеграл с переменным верхним пределом
Шкалы измерений Шкалой измерений называют упорядоченную совокупность значений физ величины, принятую по соглашению на основании результатов точных измерений 1. Шкала наименований (классификации) – основана на приписывании объекту знаков или цифр для их идентификации или нумерации. 2. Шкала порядка (ранжирования) - упорядочивает объекты относительно какого-либо их свойства в порядке убывания или возрастания 3. Шкала интервалов (разностей) содержит разность значений физической величины. Шкала состоит из одинаковых интервалов, имеет условную (принятую по соглашению) единицу измерения и произвольно выбранное начало отсчета - нуль. 4. Шкала отношений - это шкала интервалов с естественным (не условным) нулевым значением и принятые по соглашению единицы измерений. 5. Абсолютные шкалы - это шкалы отношений, в которых однозначно присутствует определение единицы измерения. Абсолютные шкалы присущи относительным единицам (коэффициенты усиления, полезного действия и др.), единицы таких шкал являются безразмерными. 6. Условные шкалы - шкалы, исходные значения которых выражены в условных единицах. К таким шкалам относятся шкалы наименований и порядка. Шкалы разностей, отношений и абсолютные называются метрическими (физическими) шкалами.
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.210.16 (0.005 с.) |




 где о — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.
где о — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.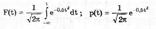
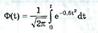 называют функцией Лапласа.
называют функцией Лапласа.


