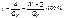Принципы оценивания погрешностей

Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Точность результата измерения характеризуется погрешностью. Погрешность измерения описывается определенной математической моделью.

Характеристики погрешности принято делить на точечные и интервальные. К точечным относятся СКО случайной погрешности и предел сверху для модуля систематической погрешности, к интервальным — границы неопределенности результата измерения. Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называются предельными интервалами.

Принципы:

Во-первых, оцениваются отдельные характеристики и параметры выбранной модели погрешности.

Во-вторых, оценки погрешности определяют приближенно, с определенной точностью.

В-третьих, погрешности оцениваются сверху, поэтому погрешность лучше преувеличить, чем преуменьшить, так как в первом случае снижается качество измерений, а во втором — возможно полное обесценивание результатов всего измерения.

В-четвертых, точность измерений должна соответствовать цели измерения. Излишняя точность ведет к неоправданному расходу средств и времени. Недостаточная точность в зависимости от цели измерения может привести к признанию годным в действительности негодного изделия, к принятию ошибочного решения и т. п.

Оценивание погрешностей может проводится до (априорное) и после (апостериорное) измерения. Априорное оценивание — это проверка возможности обеспечить требуемую точность измерений, проводимых в заданных условиях выбранным методом с помощью конкретных СИ. Оно проводится в случаях:

• нормирования метрологических характеристик СИ;

• разработки методик выполнения измерений;

• выбора средств измерений для решения конкретной измерительной задачи;

• подготовки измерений, проводимых с помощью конкретного СИ.

Апостериорную оценку проводят в тех случаях, когда априорная оценка неудовлетворительна или получена на основе типовых метрологических характеристик, а требуется учесть индивидуальные свойства используемого СИ.

 

Погрешности измерений

Отклонение результата измерения от истинного значения физической величины называется погрешностью измерения.

Истинное значение физической величины - значение физической величины, которое идеальным образом отражало бы в количественном и качественном отношениях соответствующее свойство объекта.

Поскольку определить истинное значение физической величины в принципе невозможно, то на практике вместо понятия истинного значения физической величины применяют понятие действительного значения измеряемой величины, которое настолько точно приближается к истинному значению, что может быть использовано вместо него. Это может быть, например, результат измерения физической величины образцовым средством измерения.

Погрешность измерения (результирующая погрешность) является суммой двух составляющих: систематической погрешности и случайной погрешности.

Систематическая погрешность - это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Причинами появления систематической погрешности могут являться неисправности средств измерений, несовершенство метода измерений, неправильная установка измерительных приборов, отступление от нормальных условий их работы, особенности самого оператора. Систематические погрешности в принципе могут быть выявлены и устранены. Систематические погрешности подразделяются на методические, инструментальные и субъективные.

Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Инструментальные погрешности зависят от погрешностей применяемых средств измерения. Субъективные погрешности вызываются неправильными отсчетами показаний прибора человеком (оператором). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности.

Погрешность результата измерений – это разница между результатом измерения X и истинным значением Q измеряемой величины D = X – Q. (1)

Погрешность средства измерения – разность между показанием средства измерения и истинным значением измеряемой величины.

По характеру проявления погрешности делятся на: случайные, систематические, прогрессирующие и грубые.

Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины.

Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Грубая погрешность (промах) – это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, который для единых условий резко отличается от остальных результатов этого ряда.

По способу выражения измерения погрешности бывают: абсолютная, относительная, приведенная.

Абсолютная погрешность D выражается в единицах измеряемой величины.

Относительная погрешность – это отношение абсолютной погрешности к истинному значению измеряемой величины.

Приведенная погрешность – это относительная погрешность, у которой абсол. погрешность средств измерений определена к условно принятому Q_N, постоянному во всем диапазоне измерений или его части.

где Q_N – нормирующее значение.

По зависимости абсол. погрешности от значений измеряемой величины:

1) аддитивная D_а, не зависящая от измеряемой величины;

2) мультипликативная D_м, которая прямо пропорциональна измеряемой величине;

3) нелинейная D_N, имеющая нелинейную зависимость от измеряемой.

По влиянию внешних условий: основная и дополнительная погрешность.

Основная погр-ть – в нормальных условиях эксплуатации.

Дополнительная погрешность – погреш-ть СИ, возникающая за счет отклонения от н.у. эксплуатации.

 

23. Эталоны единиц электрических величин. Эталон - это средство измерения или комплекс средств измерения, обеспечивающих воспроизведение и (или) хранения единицы ФВ с наивысшей точностью для данного уровня развития измерительной техники. Первичный эталон – обеспечивает воспроизведение единицы с наивысшей в стране точностью. Специальный эталон – обеспечивает воспроизведение единицы в особых условиях и заменяет первичный эталон. Первичный и специальный эталоны являются исходными для страны, их утверждают в качестве гос-го. Эталоны бывают: государственные, национальные, международные. Эталон свидетель – служит для проверки сохранности и неизменности гос-го эталона и замены его в случае порчи или утраты. Эталон копия – предназначен для передачи размера единиц рабочим эталонам. Его создают в случае необходимости проведения большого числа поверочных работ. Эталон сравнения – применяют для взаимного сличения эталонов, которые по тем или иным причинам нельзя непосредственно сравнивать друг с другом.

Рабочие эталоны – предназначены для поверки образцовых и наиболее точных рабочих средств измерений.

 

 

6.Показатели точности измерений и формы представления результатов Основной метрологической характеристикой метода измерений является точность измерений, под которой понимается степень приближения результата измерений к истинному значению измеряемой величины. показатели точности измерений: интервал, в котором погрешность измерения находится с заданной вероятностью; интервал, в котором систематическая составляющая погрешности измерения находится с заданной вероятностью; числовые характеристики систематической составляющей погрешности измерения; числовые характеристики случайной составляющей погрешности измерения; функция распределения составляющей погрешности измерения. Погрешности измерений не всегда требуется знать с очень высокой точностью. В частности, для технических измерений допустимой считается погрешность оценивания погрешности в 15…20 %. Так, вычислив значение погрешности 0,4359, а результата измерения — 12,7254, надо подумать, имеет ли смысл запись результата с такой погрешностью. Ведь если исходить из того, что недостоверность результата уже характеризуется десятыми долями (0,4...), то вклад последующих значащих цифр в погрешность будет все менее весом. Поэтому и необходимо ограничивать число значащих цифр в записи результата измерения. В численных показателях точности измерений и их погрешностях должно быть не более двух значащих цифр. Так, при записи наименьшие разряды числовых значений результата измерения и численных показателей точности должны быть одинаковы. В приведенном примере оценка погрешности должна быть записана как 0,43 или 0,4, а результат измерения — 12,72 или 12,7 соответственно. Расчет погрешностей округления погрешности измерения показывает, что при округлении значений погрешности до двух значащих цифр она составляет не более 5 %, а при округлении до одной значащей цифры — не более 50 %. Правила округления результатов и погрешностей измерений 1. Результат измерения округляют до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасывают до того разряда, который соответствует разряду числового значения погрешности Пример. Результат 4,0800, погрешность 0,001. Решение. Результат округляют до 4,080 2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяют. Лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают. Пример. Число 174437 при сохранении четырех значащих цифр должно быть округлено до 174400, число 174,437 — до 174,4. 3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю сохраняемую цифру увеличивают на единицу. Пример 4.7. При сохранении трех значащих цифр число 12567 округляют до 12600, число 125,67 до 126. 4. Если отбрасываемая цифра равна 5, а следующие за ней — неизвестны или нули, то последнюю сохраняемую цифру не изменяют, если она четная, и увеличивают на единицу, если она нечетная. Пример 4.8. Число 232,5 при сохранении двух значащих цифр округляют до 232, а число 233,5 до 234. 5. Погрешность результата измерения указывают двумя значащими цифрами, если первая из них равна 1 или 2, и одной — если первая цифра равна 3 или более. 6. Округление результатов измерений производят лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками