
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА 3. Законы распределения случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
График плотности нормального распределения называется +кривой Гаусса — кривой Бернулли —кривой Пауссона —кривой Лапласа
Нормальное распределение случайной величины возникает тогда, когда варьирование случайной величины обусловлено воздействием —малого числа факторов +большого числа факторов —редкими факторами —конечным заранее определенным числом факторов
Дискретная случайная величина, выражающая число появления события А в n независимых испытаниях, проводимых в равных условиях и с одинаковой вероятностью появления события в каждом испытании, называется распределенной по —нормальному закону —по закону Пуассона +биномиальному закону —по показательному закону
Если случайная величина имеет биномиальное распределение, n – число независимых испытаний, а p – вероятность наступления события, то математическое ожидание вычисляется по формуле — — — +
Если случайная величина имеет биномиальное распределение, n – число независимых испытаний, а p – вероятность наступления события, то дисперсия случайной величины вычисляется по формуле + — — —
В распределении Пуассона редких событий параметр а равен — + — —
Свойство стационарности потока событий означает, что вероятность появления k событий за промежуток времени —не зависит от числа k —не зависит от величины промежутка времени +зависит только от числа k и величины промежутка времени —не зависит ни от числа k ни от величины промежутка времени
Для расчета вероятностей ошибок при округлении показаний измерительных приборов используют + равномерное распределение —биномиальное распределение —распределение Пуассона —нормальное распределение
Функция надежности связана с —нормальным распределением —биномиальным распределением —равномерным распределением +показательным распределением
Математическое ожидание равномерно распределенной случайной величины вычисляется по формуле — + — —
Дисперсия равномерно распределенной случайной величины вычисляется по формуле — — + —
Вероятность попадания равномерно распределенной случайной величины в интервал
— —
— +
Плотность распределения случайной величины с показательным распределением имеет вид + — —
—
Функция распределения случайной величины с показательным распределением имеет вид — + —
—
У показательного распределения математическое ожидание и среднее квадратическое отклонение —всегда различны —всегда различаются на единицу +всегда равны —всегда равны 1
Если —надежность работы —скорость отказов работы —вероятность отказа +наработка на отказ
Графиком плотности распределения равномерно распределенной случайной величины является +ступенчатая функция —парабола —гипербола —экспонента
Для равномерно распределенной случайной величины параметр с вычисляется по формуле — + — —
Распределение Пуассона имеет —0 параметров —два параметра +один параметр — три параметра
Показательное распределение имеет —0 параметров —три параметра —два параметра +один параметр
Нормальное распределение имеет + два параметра —0 параметров —один параметр — три параметра
Среднее квадратическое отклонение биномиально распределенной случайной величины вычисляется по формуле — + — —
В распределении Пуассона редких событий при — — + —
В точке —точку перегиба —точку минимума —точку разрыва +точку максимума
Точки +точками перегиба —точками максимума —точками минимума —точками разрыва
Функция плотности нормального распределения с математическим ожиданием — + — —
Вероятность того, что нормально распределенная случайная величина Х, имеющая математическое ожидание а и средне – квадратическое отклонение — — + —
Вероятность того, что отклонение нормально распределенной случайной величины Х от ее математического ожидания не превзойдет по абсолютной величине
— — —
+
Распределение Пуассона характеризуется тем, что его математическое ожидание и дисперсия + равны между собой —обратно пропорциональны друг другу —оба равны 0 —отличаются друг от друга на 1
Поток событий называется простейшим, если он обладает следующими свойствами —стационарностью, отсутствием последействия, независимостью +стационарностью, отсутствием последействия, ординарностью —отсутствием последействия, периодичностью, непрерывностью —стационарностью, периодичностью, непрерывностью
Интенсивностью потока называется —общее число появления событий в наблюдаемый отрезок времени —среднее время между появлением событий +среднее число появлений событий за единицу времени —общее время между появлением событий
Случайная величина, являющаяся числом появлений событий в простейшем потоке за фиксированный промежуток времени, имеет распределение — нормальное —биномиальное —показательное +Пуассона
Непрерывная случайная величина, являющаяся промежутком времени между появлением двух событий в простейшем потоке, имеет —равномерное распределение —нормальное распределение —биномиальное распределение +показательное распределение
Параметрами нормального распределения являются +математическое ожидание и средне – квадратическое отклонение —функция распределения и функция плотности распределения —функция —дисперсия и средне – квадратическое отклонение
Если плотность распределения — нормальное распределение + равномерное распределение — показательное распределение — биномиальное распределение
Плотность нормального распределения определяется формулой — — — +
Случайная величина равномерно распределена на отрезке [2,6]. Ее дисперсия равна — —3 + —2
Случайная величина равномерно распределена на отрезке [2,8]. Ее математическое ожидание равно —2 —3 —8 +5
Случайная величина имеет биномиальное распределение с параметрами n=40 и p=0,3. Ее математическое ожидание равно —3 —18 +12 —10
Случайная величина имеет биномиальное распределение с параметрами n=20 и p=0,4. Ее дисперсия равна —9 +4,8 —13 —2,1
ТЕМА 4. Выборочный метод. Если генеральная совокупность неоднородна, то способ отбора — серийный — собственно – случайный +типический —механический
Статистическое распределение выборки – это +соответствие между вариационным и частотным рядами —вариационный ряд —частотный ряд —число вариант в вариационном ряду
Мерой колеблемости признака около среднего значения в выборочной совокупности является —предельная ошибка выборки —выборочная доля — коэффициент надежности +выборочная дисперсия
Ошибкой репрезентативности (выборки) называется —ошибка при вычислении характеристик выборочной совокупности +отклонение характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности —ошибка при вычислении характеристик генеральной совокупности —среднее квадратическое отклонение
Надежностью оценки числовой характеристики генеральной совокупности называется
+вероятность попадания этой характеристики в доверительный интервал —отношение предельной ошибки выборки к средней ошибке —доверительный интервал —точность оценки
В выборочном методе гистограмма – это графическая иллюстрация —функции распределения —функции распределения —плотности распределения +статистического распределения выборки при интервальном задании вариационного ряда —закона распределения дискретной случайной величины
К числовым характеристикам выборочной совокупности относится —предельная ошибка выборки —генеральная доля —коэффициент надежности +выборочная доля
Средняя ошибка выборки – это —выборочная средняя —выборочное среднее квадратическое отклонение +среднее отклонение характеристики выборочной совокупности от соответствующей характеристики генеральной совокупности —выборочная дисперсия
Доверительный интервал – это интервал, в который с надежностью +характеристика генеральной совокупности —характеристика выборочной совокупности —значение изучаемого признака генеральной совокупности — значение изучаемого признака выборочной совокупности
Выборочная средняя – это —значение изучаемого признака, выбранное из середины вариационного ряда +среднее взвешенное значение признака в выборочной совокупности —среднее арифметическое всех значений признака в выборочной совокупности —среднее взвешенное квадратов отклонений значений признака около среднего
Выборочная средняя равна — — + —
Величина объема выборки зависит от + требуемой точности и надежности результатов —генеральной дисперсии —выборочной средней —генеральной средней
В формуле —коэффициентом выборки + коэффициентом надежности —признаком выборки —точностью оценки
При повторном собственно – случайном отборе предельная ошибка выборки зависит от —объема генеральной совокупности —генеральной дисперсии +объема выборочной совокупности —выборочной средней
При серийном отборе под объемом выборки понимается —среднее количество элементов в серии —количество элементов в одной из серий —наибольшее количество элементов во всех сериях +количество серий, выбранных из общего количества серий
Выборочный метод опирается на
—теорему Бернулли —теорему Пуаcсона —лемму Маркова +теорему Чебышева –Ляпунова
При повторном отборе зарегистрированные и обследованные единицы +вновь возвращаются в генеральную совокупность и снова могут принять участие в дальнейшем отборе —в генеральную совокупность не возвращаются —в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут —помечаются специальным знаком
При бесповторном отборе зарегистрированные и обследованные единицы —возвращаются в генеральную совокупность +не возвращаются в генеральную совокупность —возвращаются в генеральную совокупность и могут принять участие в дальнейшем отборе — в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут
При серийном способе отбора внутри выбранной серии проводится +сплошное наблюдение —выборочное наблюдение —наблюдение первых n элементов —наблюдение последних n элементов
Типический способ отбора применяется в тех случаях, когда генеральная совокупность —состоит из малого числа элементов +неоднородна — однородна — неупорядочена
К способам отбора не требующим разделения на группы, относятся —случайный и типический способы отбора —типический и серийным способы отбора —механический и серийный способы отбора +случайный и механический способы отбора
К способам отбора требующим разделения на группы, относятся —случайный и типический способы отбора +типический и серийным способы отбора — механический и серийный способы отбора —случайный и механический способы отбора
Одной из основных задач выборочного метода является —сплошное наблюдение +определение необходимой численности выборки —подсчет количества элементов генеральной совокупности —изучение изменчивости элементов генеральной совокупности
Выборочная дисперсия по средней – это —среднее взвешенное значение квадратов признаков в выборке +среднее взвешенное квадратов отклонений значений признака около выборочной средней —среднее значение признака в выборке —наибольшее значение признака
Выборочную (по средней) дисперсию можно вычислять по формуле — + — —
При типическом отборе численность каждого типа в выборке — одинакова —равна объему выборки —обратно пропорциональна объему типа в генеральной совокупности +пропорциональна объему типа в генеральной совокупности
Частотный ряд это —совокупность выборочных значений признака —совокупность квадратов выборочных значений признака +упорядоченная последовательность частоты появлений различных значений признака — соответствие между значениями признака и числом появления этих значений
Предельная ошибка выборки — + — —
Предельная ошибка —наименьшее отклонение выборочной средней от генеральной средней —среднее отклонение выборочной средней от генеральной средней
+наибольшее отклонение выборочной средней от генеральной средней —наибольшую дисперсию
Упорядоченная последовательность вариант называется —частотным рядом — числовым рядом +вариационным рядом —функциональным рядом
В выборочном методе полигон частот – это графическая иллюстрация — функции распределения —плотности распределения —статистического распределения выборки при интервальном задании вариационного ряда +статистического распределения выборки при задании вариационного ряда в виде последовательности вариант
При возрастании объема выборки n предельная ошибка выборки +уменьшается — увеличивается —не изменяется —стремится к бесконечности
При увеличении надежности — уменьшается +увеличивается —не изменяется —стремится к 0
С вероятностью —коэффициента надежности t —средней ошибки выборки —дисперсии +предельной ошибки выборки
Величина объема выборки n зависит от +требуемых точности и надежности результатов —изучаемого признака —генеральной средней —генеральной доли
При выборочном обследовании 100 единиц совокупности, полученной собственно – случайным способом, были получены следующие данные:
Выборочная средняя равна —28 —29 —30 +31
При выборочном обследовании 100 единиц найдено среднее квадратическое отклонение —0,2 —0,02 +0,06 —0,6
При выборочном обследовании стажа работы 100 сотрудников учреждения собственно – случайным способом отбора получены данные:
Доля сотрудников, имеющих стаж работы 20 лет и более, равна —0,2 +0,4 —0,3 —0,1
Доля стандартных деталей в выборочной совокупности объемом в 100 штук, полученной путем повторного, собственно – случайного отбора, равна 0,8. С вероятностью 0,9973 предельная ошибка выборки по доле —0,08 +0,12 —0,8 —1,2
При выборочном обследовании 80 единиц совокупности, полученной путем собственно – случайного отбора, были получены следующие данные:
Выборочная средняя равна —28,6 —26,6 +25,6 —23,6
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.166.247 (0.013 с.) |


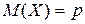
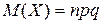

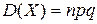
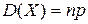


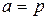




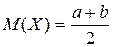








 вычисляется по формуле
вычисляется по формуле

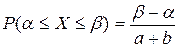
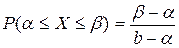




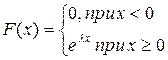
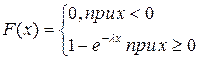


 - интенсивность отказов работы элемента, то 1/
- интенсивность отказов работы элемента, то 1/ 


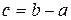








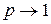
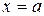 кривая Гаусса имеет
кривая Гаусса имеет и
и  являются для кривой Гаусса
являются для кривой Гаусса и средне – квадратическим отклонением
и средне – квадратическим отклонением  задается формулой
задается формулой


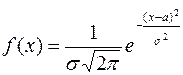
 равна
равна



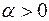 , равна
, равна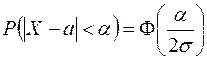



 и
и 
 непрерывной случайной величины имеет вид
непрерывной случайной величины имеет вид  , где с= const, то эта случайная величина имеет
, где с= const, то эта случайная величина имеет


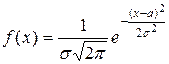


 попадает
попадает


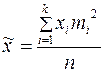
 коэффициент t называется
коэффициент t называется

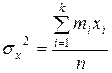

 связана со средней ошибкой
связана со средней ошибкой  формулой
формулой



 предельная ошибка выборки
предельная ошибка выборки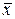 и
и  не превзойдет
не превзойдет
 . С вероятностью, равной 0,9973, предельная ошибка выборки по средней
. С вероятностью, равной 0,9973, предельная ошибка выборки по средней 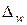 равна
равна


