Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 10. Транспортные задачи. Блокирование перевозок.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если план транспортной задачи Х= — — + —
2Модель транспортной задачи закрытая, если — + — —
Цикл в транспортной задаче – это —замкнутая прямоугольная ломаная линия, все вершины которой находятся в занятых клетках — замкнутая прямоугольная ломаная линия, все вершины которых находятся свободных клетках —замкнутая прямоугольная ломаная линия, одна вершина которой в занятой клетке, остальные в свободных клетках + замкнутая прямоугольная ломаная линия, одна вершина которой в свободной клетке, а остальные в занятых клетках
Если число занятых клеток меньше, чем (m+n-1), то одну свободную клетку делают занятой с нулевой перевозкой. Эта клетка — должна образовывать цикл с вершинами только в занятых клетках + не должна образовывать цикл с вершинами только в занятых клетках — должна образовывать цикл с вершинами только в свободных клетках — может быть любой свободной клеткой
Модель транспортной задачи является открытой, если + — — не зависит от —
Потенциалами транспортной задачи размерности (m×n) называются m+n чисел ui и vj, для которых выполняются условия + ui+vj=cij для занятых клеток — ui+vj=cij для свободных клеток — ui+vj=cij для первых двух столбцов распределительной таблицы — ui+vj=cij для первых двух строк распределительной таблицы
Оценками транспортной задачи размерности (m+n) называются числа γij=cij-ui-vj, которые вычисляются — для занятых клеток +для свободных клеток — для первых двух строк распределительной таблицы — для первых двух столбцов распределительной таблицы
Целевая функция транспортной задачи имеет вид — — — +
При составлении первоначального плана транспортной задачи по методу минимальной стоимости в первую очередь заполняются клетки — расположенные по главной диваглнали распределительной таблицы — с максимальными тарифами + с минимальными тарифами — расположенные в первых строках и столбцах распределительной таблицы
При решении транспортной задачи значение целевой функции должно от итерации к итерации — увеличиваться — увеличиваться или не меняться — увеличиваться на γij +уменьшаться или не меняться
В клетках распределительной таблицы располагаются — только тарифы перевозок cij — только планы перевозок xij +планы перевозок xij и соответствующие тарифы cij — значения поизведений cijxij
Если план транспортной задачи X=(xij)mxn является оптимальным, то оценки γij=cij-ui-vj удовлетворяют условиям — γij — γij — γij <0 для свободных клеток + γij
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид —
+
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид —
+
—
Чтобы произвести блокировку некоторой клетки транспортной задачи, в этой клетке тариф — заменяют на нуль — удваивают + заменяют на достаточно большое число М — уменьшают в два раза
Число занятых клеток невырожденного плана транспортной задачи должно быть равно — m+n — m+n+2 +m+n-1 — m+n+1
Экономический смысл целевой функции транспортной задачи —суммарный объем перевозок + суммарная стоимость перевозок —суммарные поставки — суммарные потребности
В целевой функции транспортной задачи — коэффициенты прямых затрат — коэффициенты полных затрат + стоимость перевозки одной тонны груза от i–ого поставщика к j–ому потребителю — общая стоимость перевозки от i–ого поставщика к j–ому потребителю
В целевой функции транспортной задачи — тарифы перевозок — коэффициенты полных затрат — коэффициенты прямых затрат + объем перевозимого груза от i–ого поставщика к j–ому потребителю
В транспортной задаче сумма потенциалов ui+vj равна тарифу cij, + занятых клеток — незанятых клеток — для любых клеток — для первого ряда клеток
В транспортной задаче оценки γij вы числяются для —занятых клеток — для всех клеток + для незанятых клеток —для клеток первого столбца
В транспортной задаче — максимизируется объем перевозок + минимизируется общая стоимость перевозок — минимизируется общий объем перевозок — минимизируется объем холостого пробега транспорта
Экономически отрицательная оценка —увеличится на —не изменится +уменьшится на —уменьшится на 2
Оценки транспортной задачи, вычисляемые для свободных клеток, находятся по формуле — + — —
Блокирование перевозок применяется для клетки —наибольший тариф —перевозки разрешены +перевозки запрещены —наименьший тариф
План транспортной задачи называется невырожденным, если число загруженных клеток равно — m+n-2 + m+n-1 — m+n — m+n+1
Если все оценки для свободных клеток +оптимальным —невырожденным —неоптимальным —вырожденным
Если число загруженных клеток в плане транспортной задачи меньше m+n-1, то план называется —оптимальным —неоптимальным —невырожденным +вырожденным
Блокирование перевозок применяется в транспортной задаче с открытой моделью. Если +быть вывезен полностью —частично остаться на складе —не вывозиться совсем —быть отправлен только j –му потребителю
Блокирование перевозок применяется в транспортной задаче с открытой моделью. Если —не удовлетворяться +удовлетворяться полностью — удовлетворяться частично —должны удовлетворятся полностью только i – м поставщиком
Если плану транспортной задачи —неоптимальным —вырожденным — невырожденным +оптимальным
В транспортной задаче для плана, приведенного в таблице
неоптимальной клеткой будет —(1,1) +(1,2) —(2,3) —(1,3)
Если план транспортной задачи вырожденный, то число загруженных клеток — больше, чем m+n-1 —равно m+n-1 +меньше, чем m+n-1 —равно m+n
В транспортной задаче для плана, приведенного в таблице
неоптимальной клеткой будет —(1,1) —(1,2) —(1,3) +(3,1)
Если модель транспортной задачи открытая и —дополнительный потребитель с тарифами, равными 1 +фиктивный потребитель с тарифами, равными 0 —фиктивный поставщик с тарифами, равными 0 — фиктивный поставщик с тарифами, равными 1
План транспортной задачи называется вырожденным, если число занятых клеток — равно m+n —равно m+n-1 —больше m+n-1 +меньше m+n-1 —
Дан план транспортной задачи и вычислены потенциалы:
Данный план является +оптимальным —вырожденным —неоптимальным — произвольным
Дана транспортная задача:
с открытой моделью. После приведения к закрытой модели она примет вид —
+
Дана транспортная задача:
После приведения к закрытой модели она примет вид —
+
Если в транспортной задачи +фиктивного потребителя —фиктивного поставщика — фиктивных поставщика и потребителя —нулевую поставку
Если в транспортной задачи —фиктивного потребителя +фиктивного поставщика — фиктивных поставщика и потребителя —нулевую поставку
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 3863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.70 (0.01 с.) |

 является оптимальным, то ему соответствует система
является оптимальным, то ему соответствует система  чисел, называемых потенциалами, для которых выполняются следующие условия
чисел, называемых потенциалами, для которых выполняются следующие условия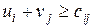 для
для  ,
,  для
для 
 для
для  для
для  для
для  для
для  для
для 





 и
и 





 0 для всех клеток
0 для всех клеток 0 для всех клеток
0 для всех клеток коэффициенты cij – это
коэффициенты cij – это ,
,  для
для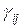 показывает что, если в клетку
показывает что, если в клетку  перебросить 1т груза, то суммарная стоимость перевозки
перебросить 1т груза, то суммарная стоимость перевозки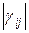




 , то план транспортной задачи будет
, то план транспортной задачи будет , то накладывается дополнительное условие, что груз i – го поставщика должен
, то накладывается дополнительное условие, что груз i – го поставщика должен соответствует система m+n чисел (потенциалов), для которых выполняются условия
соответствует система m+n чисел (потенциалов), для которых выполняются условия