
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Случайные события. Классическая вероятность.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕМА 4. Выборочный метод. Если генеральная совокупность неоднородна, то способ отбора — серийный — собственно – случайный +типический —механический
Статистическое распределение выборки – это +соответствие между вариационным и частотным рядами —вариационный ряд —частотный ряд —число вариант в вариационном ряду
Мерой колеблемости признака около среднего значения в выборочной совокупности является —предельная ошибка выборки —выборочная доля — коэффициент надежности +выборочная дисперсия
Ошибкой репрезентативности (выборки) называется —ошибка при вычислении характеристик выборочной совокупности +отклонение характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности —ошибка при вычислении характеристик генеральной совокупности —среднее квадратическое отклонение
Надежностью оценки числовой характеристики генеральной совокупности называется +вероятность попадания этой характеристики в доверительный интервал —отношение предельной ошибки выборки к средней ошибке —доверительный интервал —точность оценки
В выборочном методе гистограмма – это графическая иллюстрация —функции распределения —функции распределения —плотности распределения +статистического распределения выборки при интервальном задании вариационного ряда —закона распределения дискретной случайной величины
К числовым характеристикам выборочной совокупности относится —предельная ошибка выборки —генеральная доля —коэффициент надежности +выборочная доля
Средняя ошибка выборки – это —выборочная средняя —выборочное среднее квадратическое отклонение +среднее отклонение характеристики выборочной совокупности от соответствующей характеристики генеральной совокупности —выборочная дисперсия
Доверительный интервал – это интервал, в который с надежностью +характеристика генеральной совокупности —характеристика выборочной совокупности —значение изучаемого признака генеральной совокупности — значение изучаемого признака выборочной совокупности
Выборочная средняя – это —значение изучаемого признака, выбранное из середины вариационного ряда +среднее взвешенное значение признака в выборочной совокупности —среднее арифметическое всех значений признака в выборочной совокупности —среднее взвешенное квадратов отклонений значений признака около среднего
Выборочная средняя равна — — + —
Величина объема выборки зависит от + требуемой точности и надежности результатов —генеральной дисперсии —выборочной средней —генеральной средней
В формуле —коэффициентом выборки + коэффициентом надежности —признаком выборки —точностью оценки
При повторном собственно – случайном отборе предельная ошибка выборки зависит от —объема генеральной совокупности —генеральной дисперсии +объема выборочной совокупности —выборочной средней
При серийном отборе под объемом выборки понимается —среднее количество элементов в серии —количество элементов в одной из серий —наибольшее количество элементов во всех сериях +количество серий, выбранных из общего количества серий
Выборочный метод опирается на —теорему Бернулли —теорему Пуаcсона —лемму Маркова +теорему Чебышева –Ляпунова
При повторном отборе зарегистрированные и обследованные единицы +вновь возвращаются в генеральную совокупность и снова могут принять участие в дальнейшем отборе —в генеральную совокупность не возвращаются —в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут —помечаются специальным знаком
При бесповторном отборе зарегистрированные и обследованные единицы —возвращаются в генеральную совокупность +не возвращаются в генеральную совокупность —возвращаются в генеральную совокупность и могут принять участие в дальнейшем отборе — в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут
При серийном способе отбора внутри выбранной серии проводится +сплошное наблюдение —выборочное наблюдение —наблюдение первых n элементов —наблюдение последних n элементов
Типический способ отбора применяется в тех случаях, когда генеральная совокупность —состоит из малого числа элементов +неоднородна — однородна — неупорядочена
К способам отбора не требующим разделения на группы, относятся —случайный и типический способы отбора —типический и серийным способы отбора —механический и серийный способы отбора +случайный и механический способы отбора
К способам отбора требующим разделения на группы, относятся —случайный и типический способы отбора +типический и серийным способы отбора — механический и серийный способы отбора —случайный и механический способы отбора
Одной из основных задач выборочного метода является —сплошное наблюдение +определение необходимой численности выборки —подсчет количества элементов генеральной совокупности —изучение изменчивости элементов генеральной совокупности
Выборочная дисперсия по средней – это —среднее взвешенное значение квадратов признаков в выборке +среднее взвешенное квадратов отклонений значений признака около выборочной средней —среднее значение признака в выборке —наибольшее значение признака
Выборочную (по средней) дисперсию можно вычислять по формуле — + — —
При типическом отборе численность каждого типа в выборке — одинакова —равна объему выборки —обратно пропорциональна объему типа в генеральной совокупности +пропорциональна объему типа в генеральной совокупности
Частотный ряд это —совокупность выборочных значений признака —совокупность квадратов выборочных значений признака +упорядоченная последовательность частоты появлений различных значений признака — соответствие между значениями признака и числом появления этих значений
Предельная ошибка выборки — + — —
Предельная ошибка —наименьшее отклонение выборочной средней от генеральной средней —среднее отклонение выборочной средней от генеральной средней +наибольшее отклонение выборочной средней от генеральной средней —наибольшую дисперсию
Упорядоченная последовательность вариант называется —частотным рядом — числовым рядом +вариационным рядом —функциональным рядом
В выборочном методе полигон частот – это графическая иллюстрация — функции распределения —плотности распределения —статистического распределения выборки при интервальном задании вариационного ряда +статистического распределения выборки при задании вариационного ряда в виде последовательности вариант
При возрастании объема выборки n предельная ошибка выборки +уменьшается — увеличивается —не изменяется —стремится к бесконечности
При увеличении надежности — уменьшается +увеличивается —не изменяется —стремится к 0
С вероятностью —коэффициента надежности t —средней ошибки выборки —дисперсии +предельной ошибки выборки
Величина объема выборки n зависит от +требуемых точности и надежности результатов —изучаемого признака —генеральной средней —генеральной доли
При выборочном обследовании 100 единиц совокупности, полученной собственно – случайным способом, были получены следующие данные:
Выборочная средняя равна —28 —29 —30 +31
При выборочном обследовании 100 единиц найдено среднее квадратическое отклонение —0,2 —0,02 +0,06 —0,6
При выборочном обследовании стажа работы 100 сотрудников учреждения собственно – случайным способом отбора получены данные:
Доля сотрудников, имеющих стаж работы 20 лет и более, равна —0,2 +0,4 —0,3 —0,1
Доля стандартных деталей в выборочной совокупности объемом в 100 штук, полученной путем повторного, собственно – случайного отбора, равна 0,8. С вероятностью 0,9973 предельная ошибка выборки по доле —0,08 +0,12 —0,8 —1,2
При выборочном обследовании 80 единиц совокупности, полученной путем собственно – случайного отбора, были получены следующие данные:
Выборочная средняя равна —28,6 —26,6 +25,6 —23,6
Тема 1. Случайные события. Классическая вероятность. В формуле полной вероятности событие А является следствием одного из событий —являться единственно возможными и независимыми +образовывать полную группу событий — являться несовместными и равновозможными —являться несовместными и независимыми
В формуле Байеса событие А является следствием одного из событий — являться единственно возможными и независимыми +образовывать полную группу событий — являться несовместными и равновозможными —являться несовместными и независимыми
События образуют полную группу событий, если являются — независимыми и противоположными —единственно возможными и независимыми +несовместными и единственно возможными —несовместными и равновозможными
Обязательным условием применения формулы —независимость события А и В —события А и В единственно возможны — события А и В противоположны +совместность событий А и В
Обязательным условием применения формулы —независимость события А и В +несовместность событий А и В — события А и В единственно возможны —совместность событий А и В
Обязательным условием применения формулы —противоположность событий А и В +независимость событий А и В —несовместность событий А и В — зависимость событий А и В
Два события называются противоположными, если они —независимы — не совместны —единственно возможны +образуют полную группу событий
Суммой событий А и В называется событие С, которое происходит, если происходят —только событие А —только событие В +одно из событий А или В — оба события А и В Произведением событий А и В называется событие С, которое происходит, если происходит — только событие А —только событие В —одно из событий А или В +оба события А и В
—вероятность события А при условии, что А и В противоположные события —вероятность события А при условии, что А и В несовместные события вероятность события А при условии, что событие В произошло —произведение событий А и В
Пусть — + — —
Если некоторый объект А может быть выбран равно — + — —
Если некоторый объект А можно выбрать — + — —
Формула полной вероятности имеет вид + — — —
Вероятность невозможного события равна —1 —2 +0 —4
Вероятность достоверного события равна —2 —4 —0 +1
Вероятность — — — +
Сумма вероятностей событий, образующих полную группу, равна —0 —1/2 +1 —4
Достоверным называется событие, которое —может произойти, а может не произойти —никогда не произойдет +обязательно произойдет —происходит три раза
Невозможным называется событие, которое —может произойти, а может не произойти +никогда не произойдет —обязательно произойдет —происходит три раза
Произведено — — + —
Случайным называется событие А, которое +может произойти, а может не произойти —никогда не произойдет —обязательно произойдет —произойдет только совместно с событием
События А и В называются зависимыми, если —сумма их вероятностей обязательно равна 1 —вероятности событий А и В не зависят друг от друга +вероятность наступления одного из событий зависит от появления или не появления другого —они происходят одновременно
События А и В называются несовместными, если — вероятность наступления одного из событий зависит от появления или не появления другого +появление одного из них исключает появление другого — сумма их вероятностей никогда не равна 1 —если одновременно они могут появиться только конечное число раз
Если вероятность события А равна 0,7, то —0,8 —0,5 —0,4 +0,3
События называются единственно возможными, если они —независимы — несовместны —достоверны + одно из них обязательно происходит
Полная группа событий называется пространством элементарных событий, если события —независимы —единственно возможны +равновозможны —попарно противоположны
Рассматривается пространство из N элементарных событий. Событию А благоприятствуют M элементарных событий. Классическая вероятность события А равна — — + —
Рассматривается пространство элементарных событий. Некоторое элементарное событие благоприятствует событию А, если —они несовместны —они противоположны —они независимы +А − следствие этого элементарного события
Если вероятность события А равна нулю, то оно называется —достоверным — случайным —произвольным +невозможным
Если вероятность события А равна 1, то оно называется —произвольным +достоверным —невозможным —случайным
Какая пара событий состоит из противоположных событий —день, ночь +попадание, промах —черное, белое —большой, маленький
Если —невозможным —достоверным — единственно возможным +случайным
Уровнем значимости называется —значительная вероятность —вероятность близкая к 1 +вероятность, близкая к 0 —значительный уровень события
На склад поступает продукция трех цехов. Доли цехов соответственно равны 1) 30%; 2) 50%; 3) 20%. Процент брака в продукции первого цеха 4%, второго цеха 6%, третьего – 8%. Полная вероятность того, что случайно взятое на складе изделие – бракованное, равна —0,025 +0,058 —0,03 —0,045
Вероятность того, что размер изделия не соответствует стандарту, равна 0,7. Вероятность того, что вес изделия не соответствует стандарту, равна 0,6. Вероятность, что изделие не стандартно, равна —0,8 —0,62 +0,88 —0,53
Вероятность того, что студент Иванов сдаст сессию на «отлично», равна 0,7. Вероятность, что студент Петров сдаст сессию на «отлично», равна 0,6. Вероятность, что оба студента станут отличниками, равна —0,51 +0,42 —0,24 —0,31
Вероятность того, что первый стрелок поразит мишень, равна 0,6, второй 0,5. Вероятность, что хотя бы один из стрелков поразит мишень, равна —0,4 +0,8 — 0,7 —0,5
—0,7 —0,4 +0,2 —0,5
Вероятность наступления каждого из трех событий p=0,8. Вероятность наступления хотя бы одного из них равна —0,995 +0,992 —0,904 —0,97
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.255.122 (0.013 с.) |

 попадает
попадает


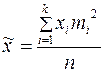
 коэффициент t называется
коэффициент t называется

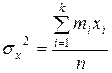

 связана со средней ошибкой
связана со средней ошибкой  формулой
формулой



 предельная ошибка выборки
предельная ошибка выборки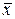 и
и  не превзойдет
не превзойдет
 . С вероятностью, равной 0,9973, предельная ошибка выборки по средней
. С вероятностью, равной 0,9973, предельная ошибка выборки по средней 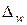 равна
равна . События
. События  обязательно должны
обязательно должны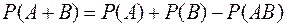 является
является является
является является
является это
это . Вероятность появления хотя бы одного из событий
. Вероятность появления хотя бы одного из событий  равна
равна



 способами, после чего объект В может быть выбран
способами, после чего объект В может быть выбран  способами, то число вариантов выбора пары А и В
способами, то число вариантов выбора пары А и В








 любого события принадлежит отрезку
любого события принадлежит отрезку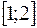











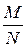

 , то событие А является
, то событие А является .
.  равна
равна


