
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели случайных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Министерство Российской Федерации По связи и информатизации
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ Им. проф. М.А.Бонч-Бруевича
А.П. Сальников
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Конспект лекций Часть 2
САНКТ-ПЕТЕРБУРГ УДК 621.391.1
Сальников А.П. Теория электрической связи: Конспект лекций, часть 2/ СПбГУТ.-СПб., 2003.– с.: ил.
Предназначено для студентов, изучающих дисциплину «Теория электрической связи». Содержит общие сведения о математических моделях случайных сигналов и помех, их преобразованиях в различных функциональных узлах. Рассмотрены задачи оптимального когерентного и некогерентного приема дискретных сообщений, реализации соответствующих демодуляторов для двоичных систем связи и определения помехоустойчивости для основных видов цифровой модуляции. Материал соответствует действующей учебной программе по курсу ТЭС.
Ответственный редактор М.Н. Чесноков
© Сальников А.П., 2003 © Издание Санкт-Петербургского государственного университета телекоммуникаций им. проф. М.А. Бонч-Бруевича, 2003 Математические модели случайных процессов Сигналы в системах передачи информации и действующие в них помехи по своей природе являются случайными процессами. Для их описания необходимо применять математический аппарат теории вероятностей и случайных процессов. Настоящую главу следует рассматривать как развитие раздела 2. Математические модели сигналов (Теория электрической связи. Конспект лекций. Часть 1) применительно к случайным процессам.
Понятие случайного процесса
Таблица 4.1
Примеры распределений случайных величин:
Информация о сечениях СП не является достаточной для описания самого СП, так как не содержит сведений о зависимостях сечений между собой. Исчерпывающее описание СП осуществляется с помощью n -мерной функции распределения
или n -мерной плотности вероятности
где x 1, x 2…, xn – аргументы, t 1, t 2…, tn – параметры этих функций, а n – любое целое число. Если n -мерная функция распределения (плотность вероятности) СП не меняется при сдвиге всех моментов tk (k = 1, 2, …, n) на один и тот же интервал D t, то такой процесс называют стационарным в узком смысле.
Сокращенное описание случайных процессов Полное описание СП не всегда возможно, да и не всегда требуется. Во многих случаях достаточно знать основные его характеристики. В качестве таковых широко используют: 1. Математическое ожидание СП – начальный момент первого порядка
2. Дисперсия СП – центральный момент второго порядка
Здесь использовано понятие центрированного СП 3. В общем случае можно использовать моменты k -го порядка: Начальные
Центральные
Нетрудно видеть, что моменты полностью определяются одномерным распределением и в общем случае произвольного СП являются детерминированными функциями времени. Для стационарных в узком смысле СП моменты от времени не зависят. 1. Корреляционная (автокорреляционная) функция – центральный смешанный момент второго порядка
Случайные процессы называют стационарными в широком смысле, если выполняются следующие условия:
Очевидно, что стационарность СП в узком смысле влечет его стационарность в широком смысле, но не наоборот. Некоторые свойства корреляционной функции СП: 1. 2. Доказательство:
откуда следует вышеуказанное неравенство 3. Корреляционная функция характеризует статистическую связь сечений СП (внутри процесса). Если связи между сечениями Доказательство:
Отсутствие связи влечет отсутствие корреляции, но не наоборот. Обратное утверждение справедливо лишь в случае нормального (гауссовского) процесса. Нормальным называют СП, у которого одномерная плотность вероятности имеет вид
где а любая n -мерная плотность вероятности описывается выражением
где An, cij, ai, aj – константы, определяемые выбором сечений t 1, t 2,,, tn. 4. Корреляционная функция стационарного случайного процесса является четной Доказательство:
Подставляя
5. Чтобы абстрагироваться от дисперсии и учитывать только связи внутри СП удобно пользоваться нормированной функцией корреляции (коэффициентом корреляции)
Очевидно, что 6. Интервал корреляции – грубую числовую оценку связи внутри СП – чаще всего определяют методом равновеликого прямоугольника
7. Взаимная корреляционная функция двух процессов X (t) и Y (t)
8. Корреляционная функция суммы независимых случайных процессов Доказательство:
- постоянную составляющую СП,
- переменную составляющую СП,
- мощность переменной состав- ляющей СП.
Нетрудно видеть, что эти характеристики являются случайными величинами, не зависящими от времени.
 Эргодическое свойство СП заключается, грубо говоря, в том, что все его реализации «похожи» друг на друга. Отсюда следует возможность получения вышеуказанных характеристик эргодического СП усреднением по времени единственной его реализации x (t), что существенно облегчает построение аппаратуры для их измерений. В частности, функцию корреляции эргодического СП можно вычислить по одной реализации с помощью следующего выражения: Эргодическое свойство СП заключается, грубо говоря, в том, что все его реализации «похожи» друг на друга. Отсюда следует возможность получения вышеуказанных характеристик эргодического СП усреднением по времени единственной его реализации x (t), что существенно облегчает построение аппаратуры для их измерений. В частности, функцию корреляции эргодического СП можно вычислить по одной реализации с помощью следующего выражения:
Рекомендации по проведению экспериментальных Преобразователи сигналов
Через безынерционные цепи
Безынерционная цепь (безынерционный функциональный узел –БФУ) полностью описывается функциональной зависимостью y = f (x), связывающей мгновенные значения воздействия x (t) и реакции y (t) в совпадающие моменты времени. В результате имеем дело с функциональным преобразованием случайного процесса Y (t) = f [ X (t)]. Для вычисления одномерной плотности вероятности реакции w (y) по известной плотности вероятности воздействия w (x) рассмотрим рис. 5.2, на котором изображены функциональная характеристика БФУ y = f (x), заданная плотность вероятности воздействия w (x) и искомая плотность вероятности реакции БФУ w (y). Учитывая, что при попадании случайной величины X в интервал (x, x+dx) случайная величина Y с вероятностью 1 попадает в соответствующий ему интервал (y, y+dy), можно написать следующее соотношение
из которого вытекает
где f -1(y) – обратная функция (x = x (y) = f -1(y)).
Примеры:
1. Линейное безынерционное преобразованиеy = f (x) = ax + b. Обратная функция
Таким образом, при линейном преобразовании случайной величины ее кривая плотности распределения смещается на величину b, а масштаб по координатным осям изменяется в |a| раз. 2. Кусочно-линейное преобразование y = f (x) (рис. 5.3). Задачу решим графически, определяя вид кривой wY (y) на отдельных интервалах оси у.
 Из рассмотрения функциональной характеристики y = f (x) с очевидностью вытекает, что Из рассмотрения функциональной характеристики y = f (x) с очевидностью вытекает, что
а) при у < 0 и у > y 2 wY (y) = 0, т. к. значения реакции у не могут выйти за пределы уровней отсечки (у = 0) и насыщения (у = y 2,); б) при 0 < у < y 1 wY (y) = 0, т. к. в этот интервал (протяженностью y 1) значения реакции попадают при единственном значении воздействия x = x 1, вероятность которого wX (x 1) dx ® 0; в) при y 1 ≤ у < y 2 г) при у = 0 д) при у = у 2 3. Преобразование при неоднозначной обратной функции
На практике встречаются ситуации, когда обратная функциональная характеристика является многозначной (рис. 5. 4). Рассуждая аналогично тому, как это делали при выводе выражения (5.1), легко убедиться в том, что в этом случае для интервала
математическое ожидание
дисперсия
Функциональное преобразование двух случайных процессов Постановка задачи: Заданы два случайных процесса X 1(t) и X 2(t) с известной совместной плотностью вероятности их значений в совпадающие моменты времени w (x 1, x 2; t). С этими процессами связаны два других СП Y 1(t) и Y 2(t) известными функциональными зависимостями
Требуется определить w (у 1, у 2; t) – совместную плотность вероятности процессов Y 1(t) и Y 2(t) в совпадающие моменты времени. Решение: По аналогии с (5.1) можно написать следующее соотношение
где J – якобиан преобразования переменных x 1, x 2 в у 1, у 2
Постановка задачи Дано: 1) X (t) = A (t)cosY(t) – узкополосный центрированный стационарный нормальный СП (на выходе ПФ), 2) Определить: 1) w (A) – одномерную плотность вероятности огибающей, 2) w (Y) – одномерную плотность вероятности фазы. Для решения этой задачи наметим три этапа: 1. Переход к аналитическому СП 2. Расчет совместной плотности вероятности 3. Определение одномерных плотностей вероятности w (A) и w (Y) по вычисленной совместной плотности вероятности Решение 1 этап. Найдем одномерную плотность вероятности
Таким образом, имеем
Докажем некоррелированность
После подстановки
Некоррелированность сечений нормальных процессов влечет их независимость, следовательно
2 этап. Расчет совместной плотности вероятности
где согласно (5.2), (5.5) и (5.6)
Следовательно, с учетом (5.3) имеем
3 этап. Определение одномерных плотностей вероятности
Окончательно
Выражение (5.8) известно как распределение Рэлея, его график приведен на рис. 5.8. На рис. 5.9 приведен график равномерного распределения фазы (5.9).
Выражение (5.7) можно представить в виде произведения (5.8) и (5.9)
из чего следует независимость огибающей A (t) и фазы w (Y) нормального СП. Рассмотрим более сложную задачу прохождения аддитивной смеси выше рассмотренного нормального СП с гармоническим сигналом через АД и ФД. Постановка задачи сохраняется прежней за исключением исходного процесса Y (t), который приобретает вид
где X (t) – центрированный нормальный СП. Поскольку
то
Запишем Y (t) в квазигармонической форме
и будем решать задачу определения плотностей вероятности w (A) и w (j) по выше приведенному плану. Предварительно запишем X (t) в квазигармонической форме и через его квадратурные компоненты
Тогда
где
Отсюда
Для нахождения
Из его выражения видно, что
и, следовательно, имеют нормальное распределение с дисперсиями
Докажем их некоррелированность (а следовательно и независимость) в совпадающие моменты времени
Здесь учтено, что B (t) и θ(t) – огибающая и фаза нормального СП являются, как выше установлено, независимыми. Таким образом,
и с учетом (5.10) и (5.11) получаем
Поскольку выражение (5.12) невозможно представить в виде произведения одномерных функций Для нахождения распределения огибающей суммы центрированного нормального СП с гармоническим сигналом проинтегрируем (5.12) по всем возможным значениям случайной фазы j(t)
Интеграл вида
известен в математике как модифицированная функция Бесселя нулевого порядка. С его учетом окончательно имеем
Выражение (5.13) называют обобщенным распределением Рэлея или распределением Райса. Графики этого выражения приведены на рис. 5.10 для следующих частных случаев: 1) U = 0 2) 3)
Из графиков видно, что чем больше отношение сигнал/шум
Выводы 1. Если мгновенные значения центрированного СП X (t) имеют нормальное распределение, то его огибающая A (t) распределена по закону Релея
а фаза Y(t) равномерно
2. Распределение огибающей аддитивной смеси центрированного нормального СП и гармонического сигнала подчиняется обобщенному распределению Рэлея (оно же распределение Райса)
Контрольные вопросы 1. Сформулируйте задачу анализа прохождения СП через заданный функциональный узел. 2. Как вычисляют плотность вероятности w (y) реакции безынерционной цепи по известной плотности вероятности w (x) воздействия? 3. Как вычисляют математическое ожидание реакции безынерционной цепи на случайное воздействие X (t)? 4. Как вычисляют дисперсию реакции безынерционной цепи на случайное воздействие X (t)? 5. Как вычисляют функцию корреляции реакции безынерционной цепи на случайное воздействие X (t)? 6. Как вычисляют совместную плотность вероятности w (у 1, у 2; t) двух СП Y 1(t) и Y 2(t), связанных известными функциональными зависимостями 7. Как меняется распределение нормального СП при его прохождении через линейную цепь? 8. Как меняется произвольное распределение СП при его прохождении через узкополосный фильтр? 9. В чем суть явления нормализации широкополосного процесса при его прохождении через узкополосный фильтр? Дайте математическое обоснование этому явлению. 10. Опишите процедуру корреляционного анализа прохождения СП через линейную цепь. 11. Дайте определение огибающей и фазы СП. 12. Дайте определения аналитическому СП, его математическому ожиданию, дисперсии и функции корреляции. 13. Каким условиям удовлетворяет стационарный аналитический СП? 14. Каково распределение огибающей центрированного нормального СП? 15. Каково распределение фазы центрированного нормального СП? 16. Каково распределение огибающей суммы центрированного нормального СП и гармонического сигнала? 17. Напишите аналитическое выражение закона Рэлея. Распределение какого СП он характеризует? 18. Напишите аналитическое выражение обобщенного закона Рэлея (закона Райса). Распределение какого СП он характеризует?
Рекомендации по проведению экспериментальных исследований Постановка задачи Дано: 1. Источник дискретных сообщений. Это значит, что известен ансамбль передаваемых сообщений
и их статистика (распределение вероятностей) 2. Модулятор. Это значит, что известны правила преобразования каждого сообщения в непрерывный сигнал и длительность сигнала T bi ® si (t); i = 1, 2,…, m; t Î (0, T). 3. Непрерывный канал. Канал задается своей математической моделью, описывающей связь его реакции Z (t) с воздействием si (t) и канальными помехами N (t), например
4. Тактовая синхронизация осуществляется идеально. Вопросы синхронизации не рассматриваются в рамках курса ТЭС, поэтому здесь и в дальнейшем всегда будем считать, что границы между сигналами si (t) в приемнике определяются точно, иначе говоря, в нем осуществляется дискретизация времени функцией d(t-kT), при которой границы тактов совпадают с границами сигналов. Требуется: Определить правило решения (решающую схему) вида
т.е. указать, каким образом на основе анализа принятой реализации z (t) СП Z (t) на каждом интервале Т следует принимать решение Дадим геометрическую трактовку этой постановке задачи (рис. 6.1). Совокупность всех возможных реализаций z (t) образует пространство принимаемых колебаний (обычно бесконечномерное пространство Гильберта L 2(T)) в котором присутствуют m различных векторов Разные правила решения (разные приемные устройства) различаются способом разбиения пространства принимаемых колебаний на области В такой постановке задача приема дискретных сообщений в канале с аддитивной, нормальной помехой была решена В.А. Котельниковым (1946 г.), заложившим основы теории потенциальной помехоустойчивости. Приемник, реализующий наилучшее разбиение пространства принимаемых сигналов по выбранному критерию качества приема, Котельников назвал идеальным, а достигаемую им помехоустойчивость, при которой обеспечивается максимум средней вероятности правильного приема при заданной модуляции, – потенциальной помехоустойчивостью. Мы будем в дальнейшем такой идеальный приемник называть оптимальным демодулятором, как это часто принято в современной теории связи. Теория потенциальной помехоустойчивости конструктивна, т.к. позволяет не только определить пределы достигаемой помехоустойчивости, но и указывает пути реализации соответствующих демодуляторов.
Критерий Неймана-Пирсона
Критерий Неймана-Пирсона применяется в двоичных системах в ситуациях, когда невозможно определить априорные вероятности отдельных сообщений, а последствия ошибок разного рода неодинаковы. Такая ситуация типична для радиолокации, где осуществляется зондирование пространства узким радиолучом и прием отраженного от цели сигнала. При этом имеют место две ситуации: 1) наличие цели – колебание на входе приемника содержит сигнал в аддитивной смеси с помехой (с неизвестной априорной вероятностью P (b 1)), 2) отсутствие цели – на входе приемника действует одна помеха (с вероятностью P (b 0) = 1 – P (b 1)). Задача приема – обнаружение сигнала на фоне помех. При ее реализации возможны два вида ошибок: 1) пропуск цели (цель есть, но отраженный сигнал не обнаружен) с условной вероятностью 2) ложная тревога (цель отсутствует, но принято решение о наличии отраженного сигнала) с условной вероятностью Очевидно, что последствия этих ошибок сильно различаются. В таком случае целесообразно стремиться к уменьшению условной вероятности ошибки, вызывающей особо тяжелые последствия (пропуск цели), что можно сделать только за счет увеличения вероятности ошибки другого вида (ложной тревоги). Ясно, что это можно делать до определенной степени, т. к. слишком большая вероятность ложной тревоги приведет к ощутимым экономическим потерям и к подрыву доверия к системе в целом. Разумный выход – зафиксировать вероятность ложной тревоги на выбранном уровне ε
и затем минимизировать вероятность пропуска цели
Минимизация (6.9) при заданной величине (6.8) достигается, если решение о наличии цели принимается при выполнении неравенства
где λ(ε) – пороговый уровень, определяемый заданной вероятностью ложной тревоги.
Контрольные вопросы
1. Сформулируйте задачу оптимального приема дискретных сообщений. 2. Дайте геометрическую трактовку задаче оптимального приема дискретных сообщений. 3. Что называют правилом решения (решающей схемой) демодулятора? 4. Что такое идеальный (оптимальный) приемник дискретных сообщений? 5. Что понимают под потенциальной помехоустойчивостью приема дискретных сообщений? 6. В чем суть теории потенциальной помехоустойчивости? Когда и кем были заложены ее основы? 7. Какой смысл вкладывают в понятие критерия качества приема дискретных сообщений? Перечислите известные Вам критерии. 8. В чем суть критерия идеального наблюдателя (критерия Котельникова)? 9. Укажите особенности критерия Котельникова. 10. Что представляет собой критерий максимального правдоподобия? Как он соотносится с критерием Котельникова? 11. Расскажите о критерии минимального среднего риска. В чем его общность? 12. При каких условиях критерий минимального среднего риска совпадает с критерием Котельникова? 13. При каких условиях критерий минимального среднего риска совпадает с критерием максимального правдоподобия? 14. В чем сущность критерия Неймана-Пирсона? В каких случаях целесообразно его использование?
На корреляторах Постановка задачи: Известны: 1. Ансамбль сигналов на выходе модулятора { si (t)}; i = 1, 2,…, m; t Î (0, T). 2. Непрерывный канал
где N (t) – квазибелый нормальный шум, т. е.
3. В качестве критерия качества приема задан критерий максимального правд
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.130.228 (0.01 с.) |


 Для полного описания сечений X (ti) СП необходимо указать законы распределения значений СП в этих сечениях. Они могут быть заданы в интегральной (функция распределения) или дифференциальной (плотность вероятности) формах. В таблице 4.1., в порядке напоминания, приведены основные сведения об этих законах и их свойствах.
Для полного описания сечений X (ti) СП необходимо указать законы распределения значений СП в этих сечениях. Они могут быть заданы в интегральной (функция распределения) или дифференциальной (плотность вероятности) формах. В таблице 4.1., в порядке напоминания, приведены основные сведения об этих законах и их свойствах.









 Равномерное
Равномерное Нормальное (гауссовское)
Нормальное (гауссовское) Распределение дискретной случайной величины
Распределение дискретной случайной величины
 ,
,

 .
. ,
, .
. .
. ,
, ,
, , где τ = t 2 – t 1
, где τ = t 2 – t 1


 ,
, и
и  нет (сечения статистически независимы), то
нет (сечения статистически независимы), то  .
.

 .
. ,
, ,
,  ,
, ,
, .
. .
. , получим
, получим .
. .
. .
. .
.
 .
. есть сумма корреляционных функций каждого из слагаемых СП в отдельности
есть сумма корреляционных функций каждого из слагаемых СП в отдельности 


 .
. Вместо усреднения по множеству реализаций случайного процесса можно ввести его усреднение по времени, определяя:
Вместо усреднения по множеству реализаций случайного процесса можно ввести его усреднение по времени, определяя: Случайные стационарные процессы называют эргодическими, если их усреднение по множеству и по времени приводит к одинаковым результатам:
Случайные стационарные процессы называют эргодическими, если их усреднение по множеству и по времени приводит к одинаковым результатам: ,
,
 из которого вытекает схема коррелометра, приведенная на рис. 4.2.
из которого вытекает схема коррелометра, приведенная на рис. 4.2. В общем случае решение задачи прохождения заданного СП через конкретную электрическую цепь – функциональный узел (ФУ) произвольной сложности предполагает определение n -мерной плотности вероятности (или функции распределения) реакции цепи Y (t) на заданное случайное воздействие X (t) (рис. 5.1). Однако общего метода решения такой задачи не существует. Поэтому ограничимся рассмотрением некоторых частных случаев.
В общем случае решение задачи прохождения заданного СП через конкретную электрическую цепь – функциональный узел (ФУ) произвольной сложности предполагает определение n -мерной плотности вероятности (или функции распределения) реакции цепи Y (t) на заданное случайное воздействие X (t) (рис. 5.1). Однако общего метода решения такой задачи не существует. Поэтому ограничимся рассмотрением некоторых частных случаев. ,
, , (5.1)
, (5.1) Дифференциалы dx, dy и производная обратной функции в полученном выражении взяты по модулю в силу свойства положительности плотности вероятности.
Дифференциалы dx, dy и производная обратной функции в полученном выражении взяты по модулю в силу свойства положительности плотности вероятности. ,
, .
. y 2
y 1
y 2
y 1
 x 1 x 2 x 0 w (y)
w (x)
x 1 x 2 x
Рис. 5.3. Кусочно-линейное преобразование случайной величины.
x 1 x 2 x 0 w (y)
w (x)
x 1 x 2 x
Рис. 5.3. Кусочно-линейное преобразование случайной величины.
 (см. пример 1);
(см. пример 1); , т. к. у = 0 для всех х < x 1;
, т. к. у = 0 для всех х < x 1; , т. к. у = у 2 для всех х > x 2.
, т. к. у = у 2 для всех х > x 2. .
.
 .
. Если при анализе прохождения СП через БФУ достаточно знать только основные характеристики распределения реакции, то их можно найти, не определяя wY (y). В частности:
Если при анализе прохождения СП через БФУ достаточно знать только основные характеристики распределения реакции, то их можно найти, не определяя wY (y). В частности: ,
, функция корреляции
функция корреляции
 .
.
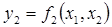 .
. ,
, . (5.2)
. (5.2) .
. и определение совместной плотности вероятности
и определение совместной плотности вероятности  .
.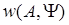 по вычисленной на первом этапе
по вычисленной на первом этапе  (5.3) ÷ (5.6).
(5.3) ÷ (5.6). процесса
процесса 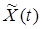 . На основе линейности преобразования Гильберта
. На основе линейности преобразования Гильберта 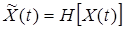 делаем вывод о том, что
делаем вывод о том, что 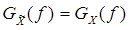 , получаем
, получаем 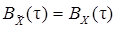 , а следовательно
, а следовательно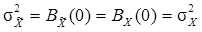 .
.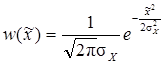 .
.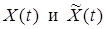 в совпадающие моменты времени, т. е. что
в совпадающие моменты времени, т. е. что  .
. .
. ,
, 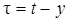 ,
, 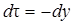 , учитывая, что при
, учитывая, что при 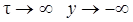 , получим
, получим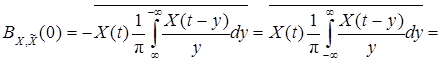
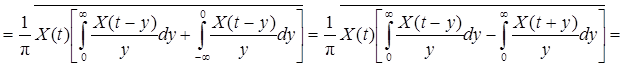
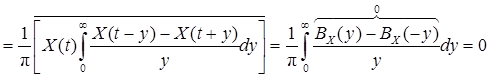 .
. .
.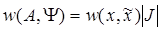 ,
,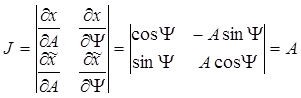 .
.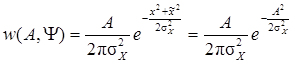 . (5.7)
. (5.7)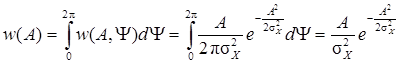 ,
,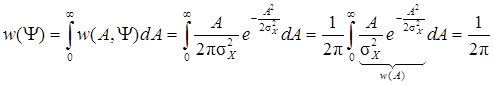
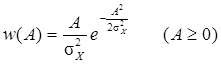 , (5.8)
, (5.8) . (5.9)
. (5.9)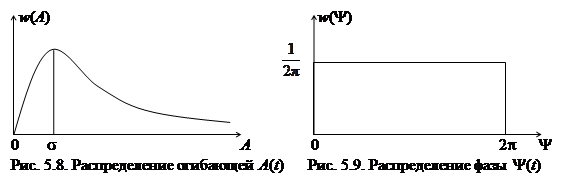
 ,
, ,
,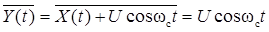 ,
, .
.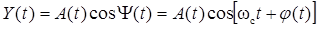
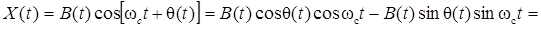
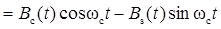 .
.

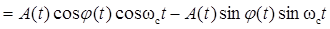 ,
,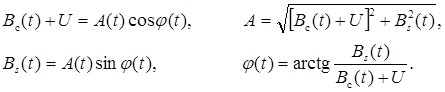
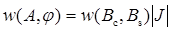 , (5.10)
, (5.10)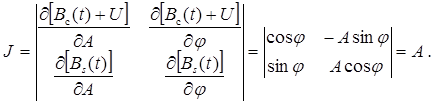 (5.11)
(5.11)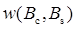 обратимся к аналитическому СП
обратимся к аналитическому СП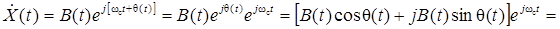
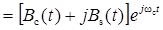 .
.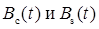 являются линейными преобразованиями центрированного нормального СП X (t):
являются линейными преобразованиями центрированного нормального СП X (t):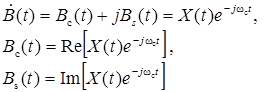
 .
.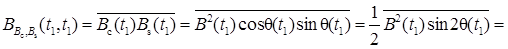
 .
.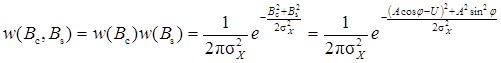
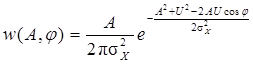 . (5.12)
. (5.12)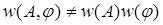 , то можно сделать вывод о зависимости процессов
, то можно сделать вывод о зависимости процессов 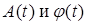 .
.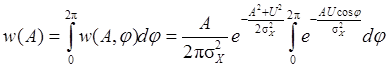 .
.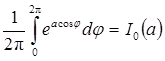
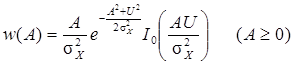 . (5.13)
. (5.13)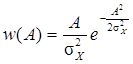 – обычное распределение Рэлея,
– обычное распределение Рэлея,
 – случай отсутствия в Y (t) СП X (t),
– случай отсутствия в Y (t) СП X (t),

 – обобщенное распределение Рэлея (Райса).
– обобщенное распределение Рэлея (Райса). тем правее смещен максимум плотности вероятности и тем симметричнее (ближе к нормальному распределению) кривая
тем правее смещен максимум плотности вероятности и тем симметричнее (ближе к нормальному распределению) кривая 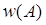 .
.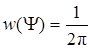 .
.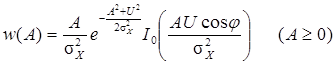 .
. , где m – объем алфавита источника
, где m – объем алфавита источника .
.
 ,
, о переданном символе bi (при j = i имеет место правильный прием, иначе (при j ≠ i) – ошибочный).
о переданном символе bi (при j = i имеет место правильный прием, иначе (при j ≠ i) – ошибочный). передаваемых сигналов si (t) (i = 1, 2,…, m). Выбор правила решения таким образом сводится к разбиению этого пространства на m непересекающихся областей
передаваемых сигналов si (t) (i = 1, 2,…, m). Выбор правила решения таким образом сводится к разбиению этого пространства на m непересекающихся областей  , каждая из которых соответствует принятию решения о передаче конкретного сообщения bi (сигналом si (t)). На рис. 6.1. показаны две ситуации: 1) конец вектора колебания
, каждая из которых соответствует принятию решения о передаче конкретного сообщения bi (сигналом si (t)). На рис. 6.1. показаны две ситуации: 1) конец вектора колебания  попадает в область
попадает в область  отведенную под решение о передаче сообщения bk сигналом sk (t), что соответствует правильному приему; 2) конец вектора колебания
отведенную под решение о передаче сообщения bk сигналом sk (t), что соответствует правильному приему; 2) конец вектора колебания  попадает в область
попадает в область  , отведенную под решение о передаче сообщения bj сигналом sj (t), что соответствует ошибочному приему.
, отведенную под решение о передаче сообщения bj сигналом sj (t), что соответствует ошибочному приему. ;
; .
. , (6.8)
, (6.8) . (6.9)
. (6.9) ,
, ,
, .
.


