
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение случайного процесса. Основные подходы к заданиюСодержание книги
Поиск на нашем сайте
Глава 1. Основные понятия теории случайных процессов Определение случайного процесса. Основные подходы к заданию Случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы. Случайным (стохастическим, вероятностным) процессом называется функция действительного переменного t, значениями которой являются соответствующие случайные величины X(t). В теории случайных процессов t трактуется как время, принимающее значения из некоторого подмножества Т множества действительных чисел (t В рамках классического математического анализа под функцией y=f(t) понимается такой тип зависимости переменных величин t и y, когда конкретному числовому значению аргумента t соответствует и притом единственное числовое значение функции y. Для случайных процессов ситуация принципиально иная: задание конкретного аргумента t приводит к появлению случайной величины X(t) с известным законом распределения (если это дискретная случайная величина) или с заданной плотностью распределения (если это непрерывная случайная величина). Другими словами, исследуемая характеристика в каждый момент времени носит случайный характер с неслучайным распределением. Значения, которые принимает обычная функция y=f(t) в каждый момент времени, полностью определяет структуру и свойства этой функции. Для случайных процессов дело обстоит совершенно иным образом: здесь совершенно не достаточно знать распределение случайной величины X(t) при каждом значении t, необходима информация об ожидаемых изменениях и их вероятностях, то есть информация о степени зависимости предстоящего значения случайного процесса от его предыстории. Наиболее общий подход в описании случайных процессов состоит в задании всех его многомерных распределений, когда определена вероятность одновременного выполнения следующих событий:
F(t1;t2;…;tn;x1;x2;…;xn) = P(X(t1)≤x1; X(t2)≤x2;…; X(tn)≤xn). Такой способ описания случайных процессов универсален, но весьма громоздок. Для получения существенных результатов выделяют наиболее важные частные случаи, допускающие применение более совершенного аналитического аппарата. В частности, удобно рассматривать случайный процессX(t, ω) как функцию двух переменных: t Неслучайная числовая функция x(t)=X(t, ω0) называется реализацией (траекторией) случайного процесса X(t, ω). Сечением случайного процесса X(t, ω) называется случайная величина, которая соответствует значению t=t0. Если аргумент t принимает все действительные значения или все значения из некоторого интервала T действительной оси, то говорят о случайном процессе с непрерывным временем. Если t принимает только фиксированные значения, то говорят о случайном процессе с дискретным временем. Если сечение случайного процесса - дискретная случайная величина, то такой процесс называется процессом с дискретными состояниями. Если же любое сечение - непрерывная случайная величина, то случайный процесс называется процессом с непрерывными состояниями. В общем случае задать случайный процесс аналитически невозможно. Исключение составляют так называемые элементарные случайные процессы, вид которых известен, а случайные величины входят как параметры: X(t)=Х(t,A1,…,An), где Ai, i=1,…,n - произвольные случайные величины с конкретным распределением.
Пример 1. Рассматривается случайный процесс X(t)=A·e-t, где А - равномерно распределенная дискретная случайная величина, принимающая значения {-1;0;1}; t≥0. Изобразить все его реализации случайного процесса X(t) и показать сечения в моменты времени t0=0; t1=1; t2=2.
Решение. Данный случайный процесс является процессом с непрерывным временем и дискретными состояниями. При t=0 сечением случайного процесса X(t) является дискретная случайная величина А{-1;0;1}, распределенная равномерно. При t=0 сечением случайного процесса X(t) является дискретная случайная величина А{-1;0;1}, распределенная равномерно. При t=1 сечением случайного процесса X(t) является дискретная случайная величина {-1/е;0;1/е}., распределенная равномерно. При t=2 сечением случайного процесса X(t) является дискретная случайная величина {-1/е2;0;1/е2}., распределенная равномерно.
Пример 2. Рассматривается случайный процесс X(t)=sin At, где А - дискретная случайная величина, принимающая значения {0;1;2}; аргумент t принимает дискретные значения {0; π/4; π/2; π }. Изобразить графически все реализации и сечения данного случайного процесса.
Решение. Данный случайный процесс является процессом с дискретным временем и дискретными состояниями.
Процессов Функция вида
Функция вида
Решение. Математическое ожидание: mY(t)=M(Xe-t)=e-tmX=me-t. Дисперсия: DY(t)=D(Xe-t)=e-2t DX=σ2e-2t. Стандартное отклонение: Корреляционная функция: KY(t1; t2)=M((X = Нормированная корреляционная функция:
По условию задачи случайная величина X распределена нормально; при фиксированном значении t сечение Y(t) линейно зависит от случайной величины X, и по свойству нормального распределения сечение Y(t) также распределено нормально с одномерной плотностью распределения:
Пример 4. Найти основные характеристики случайного процесса Y(t)=W×e-Ut (t>0), где W и U - независимые случайные величины; U распределена равномерно на отрезке [0; а]; W имеет математическое ожидание mW и стандартное отклонение σW.
Решение. Математическое ожидание: mY(t)=M(We-Ut)=MW×M(e-Ut)=mw×*M(e-Ut);
Корреляционная функция:
так как то Дисперсия:
Пример 5. Найти одномерный закон распределения случайного процесса: Y(t)=Vcos(Ψt-U), где V и U независимые случайные величины; V нормально распределена с параметрами (mV; σV); Ψ-const; U- равномерно распределена на отрезке [0; 2π].
Решение. Математическое ожидание случайного процесса Y(t):
Дисперсия:
Стандартное отклонение: Переходим к выводу одномерного закона распределения. Пусть t-фиксированный момент времени, и случайная величина U принимает фиксированное значение U=u - const; u M(Y(t)| U=u)=mV×cos(Ψt-u); D(Y(t)| U=u)= σ(Y(t)| U=u)= Так как случайная величина V распределена нормально и при заданном значении случайной величины U=u все сечения линейно зависимы, то условное распределение в каждом сечении является нормальным и имеет следующую плотность:
Безусловная одномерная плотность случайного процесса Y(t):
Очевидно, что это распределение уже не является нормальным.
Сходимость и непрерывность Сходимость по вероятности. Говорят, что последовательность случайных величин {Хn} сходится по вероятности к случайной величине Х при n®¥, если
Обозначение: Обратите внимание, что при n®¥ имеет место классическая сходимость вероятности
Случайный процесс X(t), t 3. Сходимость в среднем в степени p³1. Говорят, что последовательность случайных величин {Xn} сходится в среднем в степени p³ 1 к случайной величине Х, если
Обозначение: Xn В частности, {Xn} сходится в среднеквадратичном к случайной величине Х, если
Обозначение: Случайный процесс X(t), t
4. Сходимость почти наверное (сходимость с вероятностью единица). Говорят, что последовательность случайных величин {Хn} сходится почти наверное к случайной величине Х, если
где ωÎW - элементарное событие вероятностного пространства (W, AА, Р). Обозначение: Слабая сходимость. Говорят, что последовательность {
Обозначение:
Решение. 1) Математическое ожидание, дисперсия, стандартное отклонение, корреляционная функция и нормированная корреляционная функция случайного процесса X(t) имеют вид (см. Пример 3):
2) Переходим к расчету характеристик случайного процесса
За исключением математического ожидания (которое поменяло знак), все остальные характеристики сохранились полностью. Взаимные корреляционные функции случайного процесса X(t) и его производной
3) В соответствии с Теоремами 41-64
Взаимные корреляционные функции случайного процесса X(t) и его интеграла Y(t):
Выражение вида
где φik(t), k=1;2;…-неслучайные функции; Рассмотрим характеристики случайного процесса
Так как по условию
Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин Vк. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции:
получают значения дисперсий
Пример 7. Случайный процесс Х(t) имеет следующее каноническое разложение:
Решение. Из полученных ранее общих формул имеем:
В каждом сечении случайный процесс Х(t) имеет нормальное распределение, так как является линейной комбинацией некоррелированных нормально распределенных случайных величин Vk, при этом одномерная плотность распределения имеет вид:
Двумерный закон распределения также является нормальным и имеет следующую двумерную плотность распределения:
Пример 8. Известныо математическое ожидание mX(t) и корреляционная функция КX(t1;t2)=t1t2 случайного процесса Х(t), где
Решение. Корреляционная функция имеет следующее разложение
следовательно,
Так как то
Плотность распределения случайных величин Vk:
Каноническое разложение случайного процесса Х(t) имеет вид:
Узком и широком смыслах.
Значительное число происходящих в природе событий, в частности, связанных с эксплуатацией технических устройств, носит «почти» установившиейся характер, то есть картина таких событий, подверженных незначительным случайным флуктуациям, тем не менее, в целом с течением времени сохраняется. В этих случаях принятно говорить о стационарных случайных процессах. Например, летчик выдерживает заданную высоту полета, но разнообразные внешние факторы (порывы ветра, всходящие потоки, изменение тяги двигателей и т.п.) приводят к тому, что высота полета колеблется около заданного значения. Другим примером могла бы служить траектория движения маятника. Если бы он был предоставлен сам себе, то при условии отсутствия систематических факторов, приводящих к затуханию колебаний, маятник находился бы в режиме установившихся колебаний. Но различные внешние факторы (порывы ветра, случайные колебания точки подвеса и т.п.), не меняя в целом параметров колебательного режима, тем не менее делают характеристики движения не детерминированными, а случайными.
Стационарным (однородным во времени) называют случайный процессСП, статистические характеристики которого не меняются с течением времени, то естьт.е. являются инвариантными относительно временных и сдвигов. Различают случайные процессыСП стационарные в широком и узком смысле.
Таких, что
Выполняется условие F(t1; t2;…;tn; x1; x2;…; xn)=F(t1+τ; t2+τ;…;tn+τ; x1; x2;…; xn), и, следовательно, все n-мерные распределения зависят не от моментов времени t1; t2;…;tn, а от n-1 длительности временных промежутков τi;:
В частности, одномерная плотность распределения вообще не зависит от времени t:
двумерная плотность сечений в моменты времени t1 и t2
n-мерная плотность сечений в моменты времени t1; t2...; tn:
Случайный процессСП Хx(t) называется стационарным в широком смысле, если его моменты первого и второго порядка инвариантны относительно временного сдвига, то есть его математическое ожидание не зависит от времени t и является константой, а корреляционная функция зависит только от длины временного промежутка между сечениями:
Очевидно, что стационарный случайный процессССП в узком смысле является стационарным случайным процессомССП и в широком смысле;, обратное утверждение не верно.
ПроцессаССП 1.
2.
4. Дисперсия стационарного случайного процесса ССП есть константа, равная знзнаачению ее корреляционной функции в точке
5.
6. Корреляционная функция стационарного случайного процессаССП является положительно определенной, то есть .е.
Нормированная корреляционная функция стационарного случайного процессаССП
Пример 11. Найти характеристики и сделать вывод о типе случайного процессаСП Хx(t):
гГде U1 иb U2 - некоррелированные случайные величиныСВ;
Решение.
Следовательно, случайный процесс Х(t) является стационарным в широком смысле. Как следует из Ппримера 10…,, если U1 и U2 независимые, центрирование и нормально распределенные случайные величиныСВ, то случайный процессСП
Пример 12. … Доказать, стационарность в широком смыслечто случайного процессаСП Хx(t) является стационарным в широком смысле:
где V
Решение. Запишем Хx(t) следующим образом:
Так как случайная величина
следовательно,
Получаем
Так как cлучайный процессСП Хx(t) имеет постоянные математическое ожидание и дисперсию, а корреляционная функция является функцией
Стационарно связанные СП Cлучайные процессыСП X(t)X(t) и Y(t)Y(t) называются стационарно связанными, если их взаимная корреляционная функция зависит только от разности аргументов τ =t2-t1:
Стационарность самих случайных процессов СП X(t) X(t) и Y(t) Y(t) не означает их стационарной связанности. Отметим основные свойства стационарно связанных случайных процессовСП, производной и интеграла от стационарных случайных процессовССП, 1) 1) rRxXYy(τ)=rRyYXx(-τ). 2) 2) 3) 3) 4)4) где 5) 5) 6) 6)
Пример 13. Корреляционная функция стационарного случайного процессаССП X(t) X(t) имеет вид
Найти корреляционные функции, дисперсии, взаимные корреляционные функции случайных процессовСП X(t), Решение. Ограничимся анализом случая значениями Далее без комментариев:
Воспользуемся следующим соотношением:
Получаем:
Обратите внимание, что в результатепри дифференцированияи стационарный случайный процессССП X(t) переходит в стационарный случайный процессССП X’(t)
И их характеристики
Среди стационарных случайных процессовССП есть особый класс процессов, называемых эргодическими, которые обладают следующими свойствоами: их характеристики, полученные усреднением множества всех реализаций,совпадают с соответствующими характеристиками, полученными усреднением по времени одной реализации, наблюдаемой на интервале (0, T) достаточно большой продолжительности. То есть на достаточнобольшом временном промежутке любая реализация проходит через любое состояние независимо от того, каково было исходное состояние системы при t=0; и в этом смысле любая реализация полностью представляет всю совокупность реализаций.
Нем,
Если при этом X(t) – эргодический стационарный случайный процессССП, то
В условии теоремы
Решение.
происходят в произвольные моментты времени (см. рис.), поэтому для любого значения t с равной вероятностью ½ СП X(t) может принимать значения и +а, и –а; Поэтому одномерный закон распределе- ния каждого сечения очевиден (см. таб- лицу). Получаем
mMxХ(t)=-a·0,5+a·0,5=0; DxХ(t)=(-a)2·0,5+a2·0,5=a2.
Корреляционная функция имеет вид:
=M(X(t1)X(t2)). Произведение X(t1)X(t2) может принимать только два значения: 1) –а2, если в интервале (t1, t2) в простейшем потоке произошло нечетное число событий; 2) а2, если в интервале (t1, t2) в потоке происходит четное число событий. Вероятность k К событий на временном промежутке τ=t2-t1 (τ≥0) в простейшем потоке с интенсивностью λ находится по формуле Пуассона:
Поэтому полная вероятность всех четных kK имеет вид:
Получаем следующее значение корреляционной функции:
Окончательно,
то есть случайный процессСП X(t ) стационарен и эргодичен.
Пример 16. По заданной реализации эргодического случайного процесса X(t) найти приближенные значения его характеристик.
Решение. Временной интервал (0;20) разобьем на 10 интервалов точками 0, 2, 4,…, 20. В качестве расчетных моментов времени выбираем середины полученных интервалов:
Математическое ожидание:
Дисперсия:
Корреляционная функция:
m=0: k KX(0)≈DX=6,65 m=1:
m=2:
m=3:
m=4:
m=5:
m=6:
m=7: m=8: m=9:
Процессов ССП Случайный процесс X(t) вида X(t)=Ucosωt+Vsinωt, где U и V – центрированные некоррелированные случайные величиныСВ; DU=DV=σ2, ω – const; называется элементарным стационарным случайным процессомСП. Как следует из Примера 11, mX(t)=0; KX(t1;t2)=kKX(τ)=σ2cosωτ, τ=t2-t1; DX(t)=σ2, следовательно, X(t) – стационарный в широком смысле случайный процессСП. Часто его записывают в виде гармоники
со случайной амплитудой
Теорема Винера-Хинчина. Пусть X(t) - стационарный случайный процессССП с непрерывным временем, тогда существует и притом единственная ограниченная монотонно неубывающая функция S*(ω) такая, что корреляционная функция имеет вид.ф. имеет вид:
Если функция S*(ω) дифференцируема:
то имеюет место так называемые формулы Винера-Хинчина:
Функция Функция
Спектральная плотность sSX(ω) и корреляционная функция kKX(τ) связаны прямым и обратным косинус-преобразованием Фурье:
Функция вида
Решение. а) следовательно,
Так как ω0>0, ω≥0, то ω+ ω0>0; δ(ω+ ω0)=0. Окончательно получаем sSX(ω)=σ2δ(ω-ω0). Заметим, что в случае ω0=0: X’(t)=U; mX=0; kKX(τ)=σ2; sSX(ω)=σ2 δ(ω).
б) В соответствии с теорией
пПоэтому по аналогии с предыдущей задачей получаем
Обратите внимание на следующий факт: если случайный процессСП является суммой счетного числа гармоник, то есть имеет дискретный спектр, то
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 6015; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.106 (0.014 с.) |

 T, T
T, T  R).
R). t1, t2,…,tn
t1, t2,…,tn  T, n
T, n  T, ω
T, ω  Ω, которая при любом фиксированном значении t
Ω, которая при любом фиксированном значении t  T становится случайной величиной, определенной на вероятностном пространстве (Ω, AА, P), где Ω - непустое множество элементарных событий ω; AА - σ-алгебра подмножеств множества Ω, то есть множество событий; P - вероятностная мера, определенная на AА.
T становится случайной величиной, определенной на вероятностном пространстве (Ω, AА, P), где Ω - непустое множество элементарных событий ω; AА - σ-алгебра подмножеств множества Ω, то есть множество событий; P - вероятностная мера, определенная на AА.




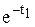 e-t1-m
e-t1-m  e-t1)×(X
e-t1)×(X  e-t2-m
e-t2-m  e-(t1+t2) M(X-m)2=σ2
e-(t1+t2) M(X-m)2=σ2 


 , (t>0).
, (t>0).



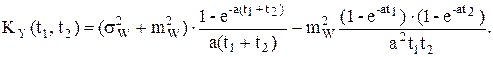


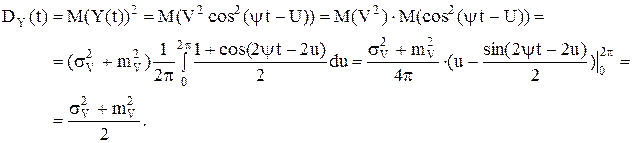

 ×cos2(Ψt-u);
×cos2(Ψt-u); ×|cos(Ψt-u)|.
×|cos(Ψt-u)|.



 к 1, то есть с возрастанием номера n можно гарантировать сколь угодно близкие к 1 значения вероятности. Но при этом нельзя гарантировать близости значений случайных величин Хn к значениям случайной величины Х ни при каких сколь угодно больших значениях n, поскольку мы имеем дело со случайными величинами.
к 1, то есть с возрастанием номера n можно гарантировать сколь угодно близкие к 1 значения вероятности. Но при этом нельзя гарантировать близости значений случайных величин Хn к значениям случайной величины Х ни при каких сколь угодно больших значениях n, поскольку мы имеем дело со случайными величинами. T называется стохастически непрерывным в точке t0
T называется стохастически непрерывным в точке t0 
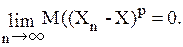
 X.
X.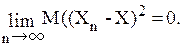
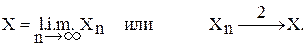


 .
. FXn(x)} функций распределения случайных величин Хn слабо сходится к функции распределения FX(x) случайной величины Х, если имеет место поточечная сходимость в каждой точке непрерывности функции FX(x).
FXn(x)} функций распределения случайных величин Хn слабо сходится к функции распределения FX(x) случайной величины Х, если имеет место поточечная сходимость в каждой точке непрерывности функции FX(x).
 X’(t). В соответствии с Tтеоремами 1-3 получаем:
X’(t). В соответствии с Tтеоремами 1-3 получаем: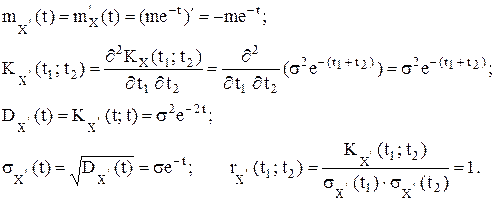

 основные характеристики интеграла от случайного процесса X(t) имеют следующие значения:
основные характеристики интеграла от случайного процесса X(t) имеют следующие значения:
 D (t1;t2)=?????????????
D (t1;t2)=?????????????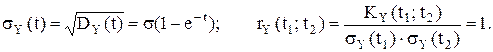

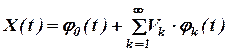 ,
,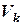 Vi, k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины
Vi, k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины 

 то
то
 . После разложения
. После разложения  в двойной ряд Фурье по координатным функциям φк(t):
в двойной ряд Фурье по координатным функциям φк(t):
 DVk случайных величин Vk.
DVk случайных величин Vk. , где Vk-нормально распределенные некоррелированные случайные величины с параметрами (0; σк); m0(t) - неслучайная функция. Найти основные характеристики случайного процесса Х(t), включая плотности распределения.
, где Vk-нормально распределенные некоррелированные случайные величины с параметрами (0; σк); m0(t) - неслучайная функция. Найти основные характеристики случайного процесса Х(t), включая плотности распределения.


 . Найти каноническое разложение Х(t) по координатным функциям
. Найти каноническое разложение Х(t) по координатным функциям  при условии, что коэффициенты разложения Vk - нормально распределенные случайные величины.
при условии, что коэффициенты разложения Vk - нормально распределенные случайные величины. ,
,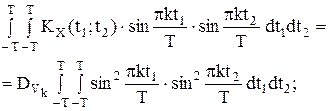 ;
; ;
; ;
; ,
, ;
;  .
.
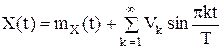 .
.








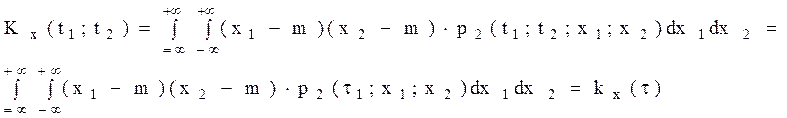 3. Корреляционная функция стационарного случайного процессаССП четна:
3. Корреляционная функция стационарного случайного процессаССП четна: поскольку она обладает следующей симметрией
поскольку она обладает следующей симметрией 
 :
:



 также четна, положительно определена и при этом
также четна, положительно определена и при этом








 также является стационарным в широком смысле.
также является стационарным в широком смысле.
 и
и  независимые случайные величиныСВ; MV=mvV - const;
независимые случайные величиныСВ; MV=mvV - const; 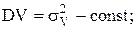
 случайная величинаСВ;
случайная величинаСВ; 








 , то вне зависимости от закона распределения случайной величиныСВ V М случайный процессСП Х x(t) является стационарным в широком смысле.
, то вне зависимости от закона распределения случайной величиныСВ V М случайный процессСП Х x(t) является стационарным в широком смысле. RxXYy(t1;t2)=rxXYy(τ).
RxXYy(t1;t2)=rxXYy(τ).





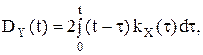 где
где 
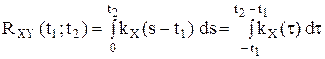 ;
;

 X’(t),
X’(t),  .
.
 DxХ(t)=1.
DxХ(t)=1.




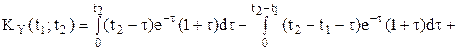

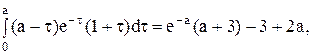
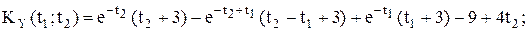





 для ССП с дискретным временем.
для ССП с дискретным временем.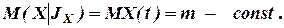
 - условное математическое ожидание случайного процессаСП X(t)относительно JYx; JYx –
- условное математическое ожидание случайного процессаСП X(t)относительно JYx; JYx – 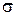 G-алгебра инвариантных по отношению к X(t)событий; событие А называется инвариантным относительно X(t), если
G-алгебра инвариантных по отношению к X(t)событий; событие А называется инвариантным относительно X(t), если  B
B 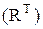 такое, что A={ω: X(ω,t)
такое, что A={ω: X(ω,t) 
 ППо смыслу задачи события в потоке
ППо смыслу задачи события в потоке


 (τ≥0).
(τ≥0). kKX(τ)→0 при τ→∞,
kKX(τ)→0 при τ→∞,
 X2(ti)
X2(ti)



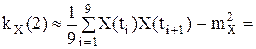
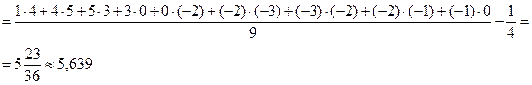
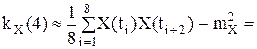



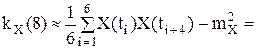

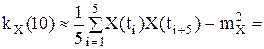

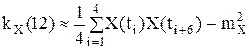 =
=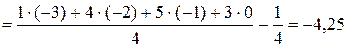







 ,
, 
 , случайной фазой ωt+arctgU/V и частотой ω.
, случайной фазой ωt+arctgU/V и частотой ω.
 ,
,

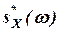 S*(ω) называется спектральной плотностью стационарного случайного процессаССП X(t) в комплексной форме.
S*(ω) называется спектральной плотностью стационарного случайного процессаССП X(t) в комплексной форме. , ω≥0 называется спектральной плотностью стационарного случайного процесса ССП X(t).
, ω≥0 называется спектральной плотностью стационарного случайного процесса ССП X(t).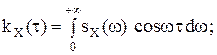 ;
; 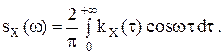 .
.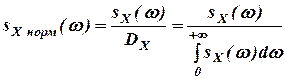
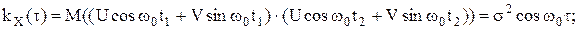
 .
. ,
, .
.


