
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумма бесконечного (счетного) числа гармоникСодержание книги
Поиск на нашем сайте
гГде Up и Vp – центрированные некоррелированные случайные величиныСВ,DUp=DVp= Как и ранее mX(t)=mX; Запись стационарного случайного процессаССП X(t) в виде суммы гармоник со случайными амплитудами, случайными фазами и фиксированными частотами называется его спектральным разложением данного ССП. Совокупность дисперсий всех гармоник стационарного случайного процессаССП называется дискретным спектром. Обычно дискретный спектр изображают в виде набора вертикальных отрезков, откладываемых от оси абсцисс в точках ωpи имеющих длину Если корреляционная функция kKX(τ) является периодической функцией с периодом 2T, то она может быть легко разложена в ряд Фурье по косинусам:
При этом коэффициенты разложения Dp образуют дискретный спектр, а координатные функции Очевидно, что если корреляционная функция kKX(τ) не обладает свойством периодичности, то стационарный случайный процессССП не обладает дискретным спектром. В этом случае ограничиваются разложением корреляционной функции в ряд Фурье на представляющем интерес отрезке [-T; T]. Но следует помнить, что увеличениеив отрезкаок: [-T; T] Каноническому разложению стационарного случайного процессаССП X(t) можно придать комплексную форму
где При этом корреляционная функция kX(τ) KX(τ) принимает вид
Непрерывный спектр. Спектральная плотность. Теорема Винера-Хинчина. Пусть X(t) - стационарный случайный процессССП с непрерывным временем, тогда существует и притом единственная ограниченная монотонно неубывающая функция S*(ω) такая, что корреляционная функция имеет вид.ф. имеет вид:
Если функция S*(ω) дифференцируема:
то имеюет место так называемые формулы Винера-Хинчина:
Функция Функция
Спектральная плотность sSX(ω) и корреляционная функция kKX(τ) связаны прямым и обратным косинус-преобразованием Фурье:
Функция вида
Называется нормированной спектральной плотностью стационарного случайного процессаССП X(t). Свойства спектральной плотности, нормированной спектральной плотности, спектральной плотности в комплексной форме. 1) 2) 3) sSX(ω)≥0; sSX норм(ω)≥0; 4) является есть плотностью распределения дисперсии стационарного случайно- го процессаССП по частоте; 5) Пусть X(t) и Y(t) – стационарные и стационарно связанные случайные процессыСП со взаимной корреляционной функцией rXY(τ). Функция sSXY(ω) вида
ННазывается взаимной спектральной плотностью. Очевидно, что rXY(τ) и s SXY(ω) связаны преобразованием Фурье:
В случае непрерывного спектра стационарный случайный процессССП X(t) имеет следующее интегральное каноническое представление:
где U(ω) и V(ω) представляют собой «белый шум», то есть
sSX(ω) – спектральная плотность. Для наиболее часто встречающихся стационарных случайных процессовССП существуют таблицы соответствия корреляционной функции kKX(τ) и спектральной плотности (в комплексной форме)
Пример 17. Найти спектральную плотность следующих стационарных случайных процессовССП: а) б) в) X(t) – стационарный «белый шум»; г) X(t) – стационарный случайный процессССП из Ппримера 15.
Решение. а) следовательно,
Так как ω0>0, ω≥0, то ω+ ω0>0; δ(ω+ ω0)=0. Окончательно получаем sSX(ω)=σ2δ(ω-ω0). Заметим, что в случае ω0=0: X’(t)=U; mX=0; kKX(τ)=σ2; sSX(ω)=σ2 δ(ω).
б) В соответствии с теорией
пПоэтому по аналогии с предыдущей задачей получаем
Обратите внимание на следующий факт: если случайный процессСП является суммой счетного числа гармоник, то есть имеет дискретный спектр, то спектральная плотность представляет собой линейную комбинацию δ-функций Дирака, принимающих бесконечное значение в точках спектра, а коэффициентами этой линейной комбинации являются соответствующие дисперсии отдельных гармоник.
в) Так как X(t) – «белый шум», то kKX(τ)=W·δ(τ), следовательно,
где W – интенсивность «белого шума».
г) ССПСтационарный случайный процесс X(t) из Примера 15примера обладает следующей корреляционной функцией
поэтому спектральная плотность sSX(ω) имеет вид:
Так как
то .
6.2. Линейные преобразования стационарного случайного процессаССП
Рассмотрим линейное преобразование Lt стационарного случайного процессаССП X(t), имеющего следующее спектральное разложение:
Получаем случайный процессСП Y(t):
имеющий характеристики mY(t)=M(Lt(mX))=Lt(mX);
где
В общем случае в результате линейного преобразования стационарного случайного процессаССП X(t) возникает нестационарный случайный процессСП Y(t). Для того, чтобы случайный процессСП Y(t) был стационарен, линейное преобразование Lt должно обладать следующими свойствами Lt(mX) – const;
Например, случайный процессСП Y(t) будет стационарен, если выполняется любая пара условий
Отметим наиболее важные в практическом отношении линейные операторы. 1.1. Оператор дифференцирования:
Очевидно, что
то есть.е. соблюдены все условия, при которых случайный процессСП Y(t) стационарен. При этом
Данные результаты легко обобщаются на случай
2.2. Оператор интегрирования: Случайный процессСП Y(t) имеет следующую структуру и характеристики:
Очевидно, что случайный процесс СП Y(t) не является стационарным.
3.3. Оператор сложения: Z(t)=X(t)+Y(t) Рассматривается сумма двух стационарных случайных процессовСП X(t ) и Y(t) с известными характеристиками mX; kKX(τ); mY; kKY(τ) и известной взаимной корреляционной функцией RXY(t1;t2).
В соответствии с общими формулами получаем: mZ(t)=mX+mY – const;
В общем случае случайный процессСПZ(t) не будет стационарным. Если жеX(t) и Y(t) стационарно связаны RXY(t1;t2)=rRXY(τ) или вообще не коррелированны RXY(t1;t2)=0, то случайный процессСП Z(t) стационарен. При этом либо
либо
Пример 18. Найти характеристики случайного процессаСП Y(t):
если mX=0;
Решение. Очевидно, что
Остановимся подробнее на процедуре дифференцированияи:
так как то Как показано в Ппримере 178 (г2), случайный процессСП X(t) имеет следующую спектральную плотность
следовательно,
. 6.3. Преобразование стационарного случайного процесса ССП стационарной Линейной системой Известно, что стационарные линейные преобразователи могут быть описаны с помощью линейных дифференциальных уравнений с постоянными коэффициентами
где X(t) – стационарный случайный процесс на входеССП на входе в систему; Y(t ) – стационарный случайный процессССП на выходе, который возникает после переходных осцилляций. В такой постановке начальные значения ССП X(t) при t=0 не играют никакой роли. Для удобства будем полагать
После применения преобразования Лапласа получаем:
где Для удобства переобозначим
тогда
Функция С(р) называется передаточной функцией стационарной линейной системы, а ее оригинал с(t) называется весовой функцией (функцией Грина) стационарной линейной системы. В соответствии со свойствами преобразования Лапласа между реализациями стационарных случайных процессовССП X(t) и Y(t) имеется следующая зависимость (называемая сверткой функций c(t) и x(t)):
Как было показано ранее, стационарный случайный процесс ССП X(t) имеет следующее каноническое разложение в комплексной форме
а его корреляционная функция имеет вид:
Рассмотрим реакцию системы на одну из гармоник, составляющих стационарный случайный процессССП, то есть x(t)=eiωt,. тогда Оочевидно, что выходной сигнал будет иметь вид y(t)=E·eiωt. Так как
Сследовательно, при возмущающем сигнале eiωt на выходе получается сигнал
Аналогично, при возмущающем сигнале
Наконец, для случайного процессаСП
получаем стационарный случайный процессССП Y(t) со следующим спектральным разложением
Выходной сигнал Y(t) имеет следующие характеристики:
где Dn=D(Wn)=D(W-n); Полученный результат допускает простое физическое толкование. При прохождении стационарного случайного процессаССП X(t) через стационарный линейный преобразователь меняются амплитуды дисперсий различных гармоник. Если Таким образомВ практическом отношении, если случайный процессСП Хx(t) и его корреляционная функция Если же известны математическое ожидание
то далее последовательно находятся
. Для наиболее распространенных выражений Пример 19. На вход стационарной линейной системы с передаточной функцией С(р) подается «белый шум» Хx(t) со следующими характеристиками: mxХ;
Решение. Из общих общенных формул получаем: чаем:
В частности, для заданной системы получаем
Знаменатель дроби может быть разложен на множители:
следовательно,
Методом неопределенных коэффициентов данное выражение можно представить как сумму следующих дробей:
Спектральная плотность случайного процессаСП Yy(t) имеет вид:
По таблице соответствий получаем
следовательно, но,
Пример 20. На вход линейной стационарной системы
подается случайный сигнал Хx(t), имеющий следующие характеристики с характеристиками: математическое ожидание mxХ и корреляционную функцию
Решение. 1. Спектральная плотность случайного процесса СП Хx(t):
2. Передаточная функция и квадрат ее модуля:
3. Спектральная плотность случайного процессаСП Y y(t):
Методом неопределенных коэффициентов получаем:
По таблице соответствий:
Задачи для самостоятельного решения 11. Задан случайный процессСП X(t)=f(t; A), где А-дискретная случайная величинаСВ, значения которой указаны в таблицеТаблице 1 (Приложение 1). Изобразить все реализации и сечения в моменты времени, указанные в таблице.
2. Найти математическое ожиданиеожидание, дисперсию, корреляционную функцию, нормированную корреляционную функцию и одномерную плотностьскость (для нормального распределенныхия случайных величин A и B) распределения сечений следующих случайного процесса Х(t),СП структура которого описана в Таблице 2 (Приложение 1). (Вво всех вариантах считать случайные величины A и B независимыми). (Пропуск в таблице означает совпадение законов распределения случайных величин А и В).
3. Найти математическое ожидание, дисперсию, корреляционную функцию и нормированную корреляционную функцию случайных процессов Х(t),
4. Задано ( см. Таблица 4, Приложение 1) каноническое разложение случайного процесса Х(t). Найти математическое ожидание, дисперсию, корреляционную функцию, одномерную и двумерную плотности распределения. Во всех вариантах
5. Случайный процесс Х(t) ( см. Таблица 5, Приложение 1) имеет известное математическое ожидание
6. Задано (см. Таблица 6, Приложение 1) каноническое разложение случайного процесса Х(t); во всех вариантах
7. Доказать, что случайный процесс X(t):
является стационарным в широком смысле и найти его характеристики;
8. Корреляционная функция стационарного случайного процесса X(t) имеет вид:
Найти корреляционные функции, дисперсии, взаимные корреляционные функции случайных процессов Х(t); 9. Рассматривается простейший поток событий с интенсивностью 10. По графику одной из реализаций эргодического стационарного случайного процесса Х(t) найти приближенные значения математического ожидания, дисперсии и корреляционной функции (см. Приложение 2). Во всех вариантах считать масштабы осей Ot и OX(t) одинаковыми;
11. Найти спектральную плотность стационарного случайного процесса Х(t), если задана корреляционная функция
12. Найти корреляционную функцию и дисперсию стационарного случайного процесса Х(t), если задана его спектральная плотность
3. Стационарная линейная система описывается следующим дифференциальным уравнением:
На вход подается стационарный «белый шум» X(t) с характеристиками:
где Wс - интенсивность «белого шума»; δ(τ) - дельта-функция Дирака. Найти характеристики выходного сигнала Y(t).
Таблица 9
14 4. На вход линейной стационарной системы:
подается стационарный случайный сигнал X(t) с математическим ожиданием mx и корреляционной функцией kKxX(τ)=e-λ|τ|. Найти характеристики выходного сигнала Y(t). Значения коэффициентов A,B,C,D взять из Ттаблицы 9задания 3. в соответствии с номером варианта.
Приложение 1
Таблица 1
|


 .
.




 позволяют записать каноническое разложение самого стационарного случайного процессаССП с точностью до mX.
позволяют записать каноническое разложение самого стационарного случайного процессаССП с точностью до mX. [-T'; T'], приводитполучаем к совершенно иномуе разложениюе, не совпадающемуе с первоначальным даже на отрезке [-T; T]. Другими словами, нет однозначности в разложении kX(τ) KX(τ) на отрезке [-T; T]; вне указанного отрезка вообще отсутствует сходимость к kX(τ) KX(τ).
[-T'; T'], приводитполучаем к совершенно иномуе разложениюе, не совпадающемуе с первоначальным даже на отрезке [-T; T]. Другими словами, нет однозначности в разложении kX(τ) KX(τ) на отрезке [-T; T]; вне указанного отрезка вообще отсутствует сходимость к kX(τ) KX(τ).






 ,
,

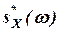 S*(ω) называется спектральной плотностью стационарного случайного процессаССП X(t) в комплексной форме.
S*(ω) называется спектральной плотностью стационарного случайного процессаССП X(t) в комплексной форме. , ω≥0 называется спектральной плотностью стационарного случайного процесса ССП X(t).
, ω≥0 называется спектральной плотностью стационарного случайного процесса ССП X(t).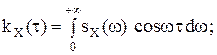 ;
; 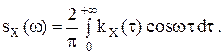 .
.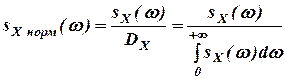


 , то естьт.е. спектральная плотность
, то естьт.е. спектральная плотность .
.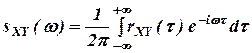
 ;
; 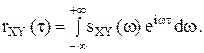 .
.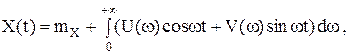 ,
,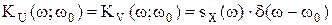 ,
, (см. Приложение 3).
(см. Приложение 3).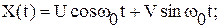 - элементарный ССП; ω0>0; X(t) – элементарный ССП;
- элементарный ССП; ω0>0; X(t) – элементарный ССП; ;
;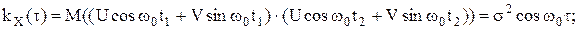
 .
. ,
, .
. ,
,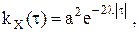 ,
,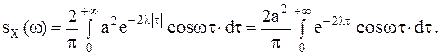 .
. ,
,
 .
. ,
,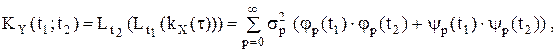 ,
,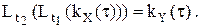 .
. ; или
; или 






 :
:

 .
.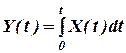

 ;
;
 ;
; .
.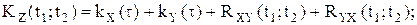

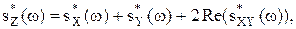
 ,
, .
. ,
, ; a, λ – const; λ>0.
; a, λ – const; λ>0. ;
; .
.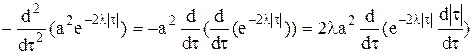 ;
; ,
, 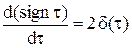 , то
, то
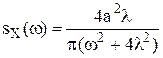 ,
,
 ,
, .
. ,
, и
и  - соответственно изображения стационарных случайных процессов ССП X(t) и Y(t).
- соответственно изображения стационарных случайных процессов ССП X(t) и Y(t). ;
; 


 ,
, .
. , то дифференциальное уравнение принимает вид
, то дифференциальное уравнение принимает вид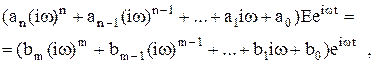 где
где ,
, .
. получаем
получаем .
.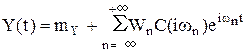 ;
;  .
.
 ;
; ;
;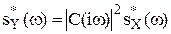 ,
, .
.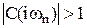 , то соответствующая дисперсия вырастает; если
, то соответствующая дисперсия вырастает; если  , то уменьшается. Так как все гармоники имеют математическое ожидание равное 0, то уменьшение дисперсии означает, что эта гармоника фактически удаляетсякак бы удаляется (отфильтровывается) из выходного сигнала.
, то уменьшается. Так как все гармоники имеют математическое ожидание равное 0, то уменьшение дисперсии означает, что эта гармоника фактически удаляетсякак бы удаляется (отфильтровывается) из выходного сигнала. заданы в виде спектрального разложения, то приведенные выше формулы полностью решают вопрос о спектральном разложении случайного процессаСП Yy(t) и расчете его характеристик.
заданы в виде спектрального разложения, то приведенные выше формулы полностью решают вопрос о спектральном разложении случайного процессаСП Yy(t) и расчете его характеристик. , корреляционная функция
, корреляционная функция 
 ;
;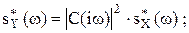 и
и и дисперсия
и дисперсия 
 составлены таблицы соответствия с
составлены таблицы соответствия с 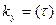 .
. . Найти характеристики выходного сигнала Yy(t). Рассмотреть частный случай системы, которая описывается следующим дифференциальным уравнением:
. Найти характеристики выходного сигнала Yy(t). Рассмотреть частный случай системы, которая описывается следующим дифференциальным уравнением:


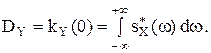
 .
.

 .
. .
. .
.



 Найти характеристики выходного сигнала Yy(t).
Найти характеристики выходного сигнала Yy(t).

 .
. .
.
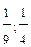
 ; 1
; 1


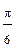
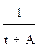


 ; 0; 1
; 0; 1



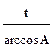




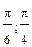
 ,
,  ( см. Таблица 3, Приложение 1). Найти взаимные корреляционные функции случайных процессов Х(t) и
( см. Таблица 3, Приложение 1). Найти взаимные корреляционные функции случайных процессов Х(t) и 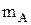 и дисперсией
и дисперсией  .
. - независимые нормально распределенные случайные величины с параметрами (0;1).
- независимые нормально распределенные случайные величины с параметрами (0;1). и корреляционную функцию
и корреляционную функцию  . Найти каноническое разложение Х(t) по координатным функциям
. Найти каноническое разложение Х(t) по координатным функциям  при условии, что коэффициентами разложения являются нормально распределенные случайные величины
при условии, что коэффициентами разложения являются нормально распределенные случайные величины  .
. . Найти математическое ожидание, дисперсию, корреляционную функцию и построить каноническое разложение случайного процесса Y(t):
. Найти математическое ожидание, дисперсию, корреляционную функцию и построить каноническое разложение случайного процесса Y(t):

 - независимые случайные величины;
- независимые случайные величины; 

 - равномерно распределенная на отрезке
- равномерно распределенная на отрезке  случайная величина;
случайная величина;  - const. Значения констант А и В взять из Таблицы 6 (Приложение 1).
- const. Значения констант А и В взять из Таблицы 6 (Приложение 1).
 . В момент наступления очередного события в потоке случайный процесс Х(t) принимает одно из значений непрерывной случайной величины А. Считая все сечения независимыми, найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса Х(t). Тип и параметры случайной величины А взять из Таблицы 2 (Приложение 1).
. В момент наступления очередного события в потоке случайный процесс Х(t) принимает одно из значений непрерывной случайной величины А. Считая все сечения независимыми, найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса Х(t). Тип и параметры случайной величины А взять из Таблицы 2 (Приложение 1). .
. (см. Таблица 7, (Приложение 1).
(см. Таблица 7, (Приложение 1). (см. Таблица 8, Приложение 1).
(см. Таблица 8, Приложение 1).





 +A
+A











