Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральным каноническим представлением случайного процесса Х(t) называется выражение видаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где
Корреляционная функция такого случайного процесса имеет вид:
Можно показать, что существует неслучайная функция G(λ) такая, что
где G(λ1) - плотность дисперсии; δ(х) - дельта-функция Дирака. Получаем Следовательно, дисперсия случайного процесса Х(t):
4.3. Линейные и нелинейные преобразования случайных процессов
Рассматривается следующая задача: на вход системы (устройства, преобразователя и т.д.) S подается «входной сигнал», имеющий характер случайного процесса Х(t). Система преобразовывает его в «выходной сигнал» Y(t):
Формально преобразование случайного процесса Х(t) в Y(t) может быть описано с помощью так называемого оператора системы Аt: Y(t)=At(Х(t)). Индекс t показывает, что данный оператор осуществляет преобразование по времени. Возможны следующие постановки задачи о преобразовании случайного процесса. 1. Известны законы распределения или общие характеристики случайного процесса Х(t) на входе в систему S, задан оператор Аt системы S, требуется определить закон распределения или общие характеристики случайного процесса Y(t) на выходе системы S. 2. Известны законы распределения (общие характеристики) случайного процесса Х(t) и требования к случайному процессу Y(t); надо определить вид оператора Аt системы S, наилучшим образом удовлетворяющего заданным требованиям к Y(t). 3. Известны законы распределения (общие характеристики) случайного процесса Y(t) и задан оператор Аt системы S; требуется определить законы распределения или общие характеристики случайного процесса Х(t).
Операторы системы
Линейные L Нелинейные N
Линейные однородные L0 Линейные не однородные Lн
1. Рассмотрим воздействиеСлучай линейной неоднородной системы Lн(...)=L0(…)+φ(t) на случайный процесс Х(t), имеющий следующее каноническое разложение:
Получаем:
введем обозначения
тогда получаем следующее каноническое разложение Y(t) приобретает вид:
Математическое ожидание случайного процессаY(t):
корреляционная функция случайного процесса Y(t):
следовательно,
С другой стороны
Дисперсия случайного процесса Y(t):
В заключении этого пункта отметим, что операторы дифференцирования и интегрирования случайных процессов являются линейными однородными.
2. Рассматривается квадратичное преобразование: Y(t)=(X(t))2,
Vk-центрированныеие случайные величины, имеющиее симметричное относительно нуля0 распределение; любые четыре из них независимы в совокупности. Тогда
Введем неслучайные функции
и случайные величины
тогда случайный процесс Y(t) приобретает вид
Представляем возможность читателю самостоятельно доказать центрированность и некоррелированность случайных величин Vk; Uk; Wkm,; k,m=1,...,n. Это, в свою очередь, означает, что получено каноническое разложение случайного процесса Y(t). Корреляционная функция Y(t):
Дисперсия:
Пример 9. Случайный процесс Х(t) имеет следующую структуру
где Vk центрированные некоррелированные случайные величины с дисперсиями
Решение. Очевидно, что Cслучайный процесс Х(t) имеет следующие характеристики:
ПосколькуОчевидно также, что случайный процесс Y(t) -является есть результатом преобразования линейнымого однороднымого операторомпреобразования случайного процесса Х(t),; воспользуемся полученными ранее в соответствии с общими формулами: получаем
Каноническое разложение случайного процессаСП Y(t y(t) имеет вид:осуществляется с коэффициентами Vk:
Пример 10. Задан случайный процессСП Хx(t) следующего вида:
где U1,U2 - независимые нормально распределенные случайные величиныСВ с параметрами (0;
Решение.
Так как
тТо случайный процессСП Yy(t) может быть записан в такой форме:
где Очевидно, что случайные величиныСВ
Покажем, что они попарно некоррелированные:. Так как
ат.к.
Таким образом, получено каноническое разложение случайного процессаСП Yy(t):.
где Так как в случае нормального распределения
то(докажите!!!), То
Следовательно,
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.237.228 (0.006 с.) |


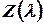 - случайная центрированная функция;
- случайная центрированная функция; 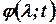 - неслучайная функция непрерывных аргументов
- неслучайная функция непрерывных аргументов 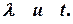
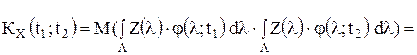
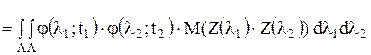 .
.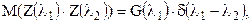
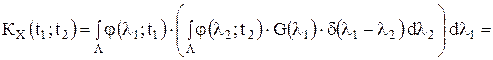
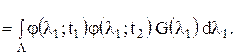
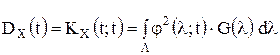 .
.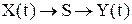 .
.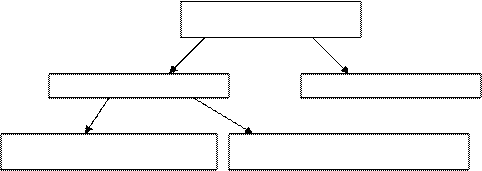 Принята следующая классификация операторов Аt системы S:
Принята следующая классификация операторов Аt системы S: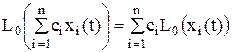
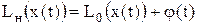
 .
.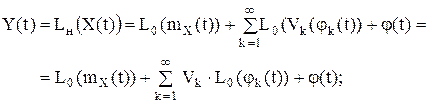
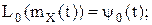
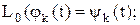
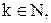
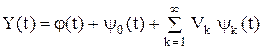 .
.
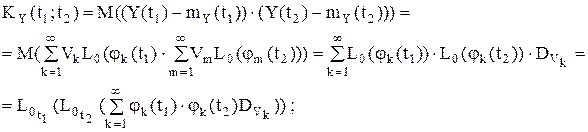
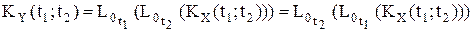 .
.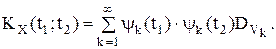

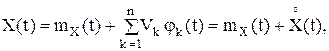 , где
, где
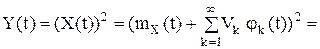

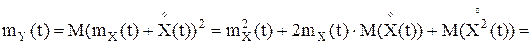

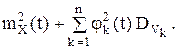

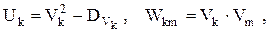
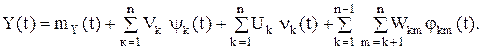
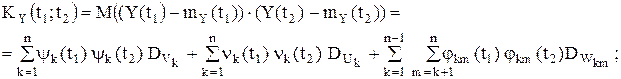
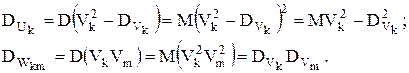
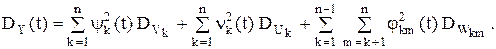
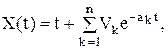
 ; акk –const;
; акk –const; 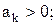 kк=1,2…;n. Найти характеристики и составить каноническое разложение случайного процесса Y(t):
kк=1,2…;n. Найти характеристики и составить каноническое разложение случайного процесса Y(t):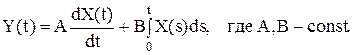
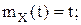

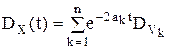 .
.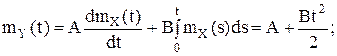
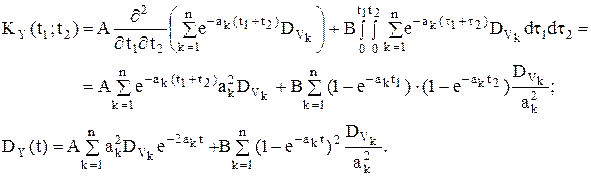
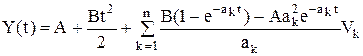 .
.
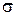 5);
5);  . Найти каноническое разложение и характеристики случайного процессаСП Y y(t):
. Найти каноническое разложение и характеристики случайного процессаСП Y y(t): 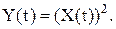

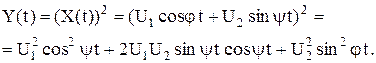
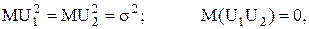
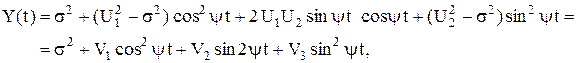
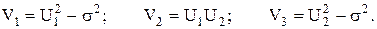
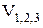 центрированы:
центрированы: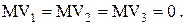
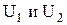 независимы и центрированы, то
независимы и центрированы, то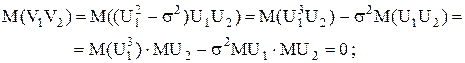
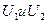 независимы и центрированы. Аналогично,
независимы и центрированы. Аналогично, 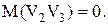

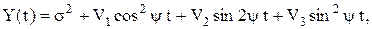
 Так как
Так как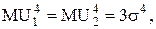 (докажите!)
(докажите!)