
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические элементы спектральной теории сигналов и теории случайных процессовСодержание книги
Поиск на нашем сайте
Методы модуляции сигналов в системах связи
Модуляция представляет собой преобразование сообщения (первичного сигнала) B(t) в сигнал U(t), пригодный для передачи по данной линии связи. При этом преобразовании осуществляется согласование источника сообщений с каналом связи. Для передачи информации требуется, чтобы сигналы имели два вида параметров: параметры селекции (отбора) и информационные параметры. Параметры селекции позволяют выделить полезный сигнал из совокупности сигналов помех. Информационные параметры служат для переноса информации – в изменении этих параметров отражаются сообщения. Управление информационными параметрами переносчика в соответствии с законом изменения передаваемого сигнала (сообщения) называют модуляцией. Пусть сигнал-переносчик это X(t), а передаваемый сигнал B(t). Тогда модуляция – это преобразование двух сигналов X(t) и B(t) в один модулированный сигнал U(t): U(t) = M[X(t), B(t)]. Для выделения переданного сигнала B(t) из U(t) необходимо выполнить преобразование обратное модуляции, т.е. демодуляцию:
Если под воздействием передаваемого сигнала B(t) информационный параметр сигнала-переносчика X(t) изменяется непрерывно, то все возможные виды модуляции являются непрерывными. К ним относят фазовую, амплитудную и частотную модуляцию и их комбинации. Так, если сигнал-переносчик – это гармоническое колебание, то имеем амплитудную, фазовую и частотную модуляцию гармонического колебания. Если в роли переносчика используют периодическую последовательность импульсов, то модуляция является импульсной: амплитудно-импульсная, частотно-импульсная. Если при модуляции информационный параметр переносчика X(t) принимает счетное число значений, то модуляцию называют дискретной. К ней относят амплитудную, фазовую и частотную манипуляцию. Если эти счетные значения пронумеровывают и в виде цифр передают по линии связи, то говорят о цифровой модуляции, например, импульсно-кодовая модуляция, дельта модуляция. В целом, в зависимости от характера передаваемого сигнала B(t) и переносчика X(t) (случайный стационарный процесс, случайный нестационарный процесс), вида этих сигналов (непрерывные, дискретные) и вида информационного параметра (амплитуда, частота, фаза, форма, длительность, период и т.д.) может быть предложено множество различных методов модуляции. Однако перечисленные выше методы непрерывной и дискретной амплитудной, фазовой и частотной модуляции, а также цифровой модуляции наиболее исследованы и нашли широкое практическое применение. Рассмотрим более детально некоторые из них.
Математические элементы спектральной теории сигналов и теории случайных процессов Разработка математических моделей сигналов и каналов связи направлена на определение структуры и параметров операторов преобразования сигналов в каналах связи, анализ свойств каналов и искажений сигналов под действием помех, синтез каналов с требуемыми свойствами. На практике, для анализа реальных, часто весьма сложных сигналов, используется их представление в виде совокупности более простых сигналов. Например, реальный сигнал можно задать в виде суммы ортогональных составляющих:
где (t1,t2) – интервал действия сигнала. Обычно система ортогональных функций yn(t) априори известна и тогда сигнал f(t) полностью определяется набором весовых коэффициентов an. Обычно в инженерных расчетах число n весовых коэффициентов an конечно. Такой конечный набор чисел an называют спектром сигнала. Для детерминированных сигналов наибольшее распространение получили методы представления, основанные на преобразовании Фурье. Тригонометрическая форма записи ряда Фурье:
Здесь Таким образом, используя разложение в ряд Фурье мы переходим от представления функции f(t) во времени, к частотной форме представления. При этом зависимость Пример: Периодическая прямоугольная функция, представленная на рисунке 1.4.
Рис.1.4.
Функция f(t) – четная, поэтому коэффициенты bn при sin равны 0. При n=0,
Амплитудный спектр f(t), показан на рис.1.5
Рис.1.5. Фазовый спектр yn изменяется от 0 до p для всех значений n, начиная от 0 при nw=0. В практических приложениях могут использоваться и другие формы записи ряда Фурье:
где т.е. Здесь, как и ранее, множество коэффициентов an, bn образует спектр (амплитудный) функции f(t), т.е. спектр сигнала. Коэффициенты an – это эффективные значения составляющих спектра, поэтому средняя мощность сигнала, выделяемая на сопротивлении 1 Ом при прохождении через него тока f(t), равна
т.е. мощность сигнала равна сумме мощностей всех составляющих его спектра. Для реальных сигналов всегда можно указать такое, обычно небольшое число n, при котором 80-90% мощности сигнала сосредоточено в гармониках с номерами n<<¥. Взаимная мощность двух сигналов f1(t) и f2(t):
и взаимная энергия двух сигналов:
где Эти характеристики полезны для изучения взаимосвязей между сигналами. Они характеризуют степень сходства сигналов. Если два сигнала совпадают, то Р12 = Р21 = Р, а сигналы f1(t) и f2(t) называют когерентными. Когда f1(t) и f2(t) ортогональны, т.е. Р12 = Р21 = 0 – сигналы некогерентные. Наряду с представлением сигналов в форме рядов Фурье важное значение имеют ортогональные разложения Котельникова для непрерывных сигналов с ограниченными спектрами, т.к. они позволяют представить такой непрерывный сигнал в виде импульсной последовательности. Теоретической основой такого разложения служит теорема Котельникова (теорема отсчетов): любая непрерывная функция f(t), не содержащая частот выше F, полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал Разложение Котельникова для непрерывного сигнала f(t), спектр которого (обычно часть спектра, где сосредоточено 80-95% энергии сигнала) лежит в интервале (0, F) имеет вид:
где fn – отсчеты сигнала в момент tn;
Энергия непрерывного сигнала с ограниченным спектром определяется через отсчеты сигнала по формуле:
Таким образом, зная длительность сигнала Т и его граничную частоту F легко определить требуемое число отсчетов n = 2FT и интервал между ними Например, телефонные непрерывные сигналы имеют 95% энергии в полосе частот от 300 до 3400 Гц. Если считать верхней частотой F=3400 Гц, то дискретизацию таких непрерывных сигналов можно производить с частотой 2F = 6800 Гц. Изложенные выше результаты относятся к математическому описанию сигналов как детерминированных функций от параметров времени или частоты. Реальные сигналы всегда носят случайный характер. Поэтому рассмотрим основные элементы математического описания сигналов как случайных процессов. Детерминированные сигналы полностью заданы и о них имеется исчерпывающая информация о том, что они из себя представляют и как они себя ведут во временной или частотной области. В отличие от них для случайных сигналов нет полной информации об их характеристиках и свойствах. Однако для таких сигналов могут быть получены достаточно определенные и предсказуемые характеристики в процессе их наблюдения за достаточно длительный период времени. Такими характеристиками являются различные средние значения: математическое ожидание, дисперсия, корреляционная функция, спектральные плотности мощности сигнала и другие. Разработкой методов получения средних характеристик случайных сигналов занимается теория случайных процессов. Рассмотрим важнейшие элементы этой теории. Каждое сообщение и соответствующий ему сигнал передаваемый по каналу связи есть элемент некоторого множества сообщений. Каждое сообщение Аi (сигнал) возникает с определенной вероятностью Pi. Множество, на котором задана вероятностная мера, называют ансамблем. Ансамбль {X(t)} непрерывных функций времени является случайным процессом. Каждая входящая в такой ансамбль функция Xr(t) является выборочной функцией или реализацией процесса. Наличие различных реализаций позволяет сообщению и сигналу переносить информацию. Если случайный процесс задан на дискретном множестве значений t1, t2, …, то он называется случайной последовательностью. Случайный процесс X(t) полностью задан, если для любого набора моментов времени t1, …, tn и любых значений X1, …, Xn можно вычислить вероятность того, то X(t) принимает в указанные моменты времени значения, не превышающие X1, …, Xn:
где X(tr), (r=1,…,n) – случайная величина, называемая сечением случайного процесса X(t) в момент времени tr; Функция F – n-мерная функция распределения вероятности процесса. То есть случайный процесс полностью задан если для любого n и любых моментов t1, …, tn можно найти его функцию распределения вероятностей F. Если существуют частные производные функции распределения вероятностей F
для любого числа n и любых моментов времени tn, то они определяют n-мерную плотность распределения вероятности и также полностью определяют случайный процесс.
Основные характеристики случайных процессов
Среднее значение случайного процесса по ансамблю или его математическое ожидание определяется как:
где Разность между случайным процессом X(t) и его математическим ожиданием
Математическое ожидание квадрата центрированного процесса называется дисперсией случайного процесса X(t):
которая также является функцией времени. Корреляционная функция K(t1, t2) определяется как математическое ожидание произведения двух сечений X1 и X2 центрированного случайного процесса (в моменты времени t1 и t2)
и определяет взаимосвязь (корреляцию) значений X1 и X2 одного случайного процесса X(t) в моменты времени t1 и t2. Поэтому эту функцию еще называют автокорреляционной. Кх(t1, t2) – функция двух моментов времени. Взаимосвязь значений X1 и X2 двух случайных процессов X1(t) и X2(t) в моменты t1 и t2 определяется функцией взаимной корреляции:
Случайный процесс, у которого математическое ожидание и дисперсия не зависят от времени, а функция корреляции зависит от разности t = t2 – t1, но не от самих значений t1 и t2 называется стационарным. Такие процессы, рассматриваемые на протяжении не слишком длительного времени, широко используются на практике в качестве математических моделей реальных сигналов и помех. При экспериментальных исследованиях характеристики случайных процессов получают чаще всего усреднением не по ансамблю, а по времени. Оценка математического ожидания случайного процесса X(t) по его i-ой реализации Xi(t) длительностью Т:
Оценка корреляционной функции:
Характеристики Стационарные случайные процессы, у которых средние по времени совпадают в пределе со средними по ансамблю, называют эргодическими. Эти процессы имеют важное практическое значение, т.к. наблюдение за большим числом реализаций случайного процесса можно заменить наблюдением за одной, но достаточно продолжительной реализацией. Также как и для случая детерминированных сигналов на практике бывает полезно сделать переход из временной в частотную область. Однако применение преобразования Фурье для случайных процессов связано с определенными затруднениями. Чтобы их обойти необходимо отбрасывание некоторых параметров спектра, а именно спектра фаз. Тогда возможно преобразование Фурье для случайных процессов и построение функций, характеризующих распределение энергии случайного процесса по оси частот. Такой функцией является спектральная плотность энергии случайного процесса. Что это такое? Для каждой реализации X(t) случайного процесса существует случайная спектральная плотность распределения
Каждая реализация этой плотности имеет энергию
где Усредняя эту функцию по всем реализациям, получим спектральную плотность распределения энергии всего случайного процесса
Кривая, изображающая функцию спектральной плотности распределения энергии процесса, охватывает площадь, равную математическому ожиданию энергии случайного процесса. Следует сказать, что знание рассмотренных средних характеристик сигнала X(t) как случайного процесса в общем случае еще не позволяет однозначно определить этот сигнал. В то же время, даже если знание этих средних не позволяет полностью описать сигнал на входе канала связи, их может быть достаточно для вычисления аналогичных средних параметров для выходного сигнала. В заключении отметим, что спектральная плотность S(2pf) или S(w) связана с корреляционной функцией К(t) соотношением Хинчина-Винера
где w = 2pf.
Интегральная характеристика спектральной плотности случайного процесса – ширина спектра.
где D – дисперсия; Sm – максимальное значение S(w).
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.007 с.) |

 .
. ,
,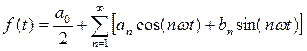 , (1.1)
, (1.1) ,
,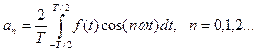 , (1.2)
, (1.2) . (1.3)
. (1.3)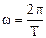 – угловая частота (радиан/секунду). Зачастую удобно использовать частоту в герцах (число периодов Т в секунду т.е.
– угловая частота (радиан/секунду). Зачастую удобно использовать частоту в герцах (число периодов Т в секунду т.е. 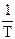 )
) 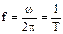 .Для этого в выражениях (1.1), (1.2), (1.3) полагаем wt=2pft (любая периодическая функция с периодом Т может быть выражена через параметр времени t, если учесть, что угол Q меняется в течение периода Т в соответствии с соотношением
.Для этого в выражениях (1.1), (1.2), (1.3) полагаем wt=2pft (любая периодическая функция с периодом Т может быть выражена через параметр времени t, если учесть, что угол Q меняется в течение периода Т в соответствии с соотношением 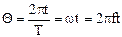 ).
).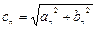 от nω - амплитудный спектр функции f(t). Зависимость ψn = arctg(bn/an) от nω - фазовый спектр функции f(t).
от nω - амплитудный спектр функции f(t). Зависимость ψn = arctg(bn/an) от nω - фазовый спектр функции f(t).

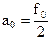 . Тогда ряд Фурье для f(t) будет иметь вид:
. Тогда ряд Фурье для f(t) будет иметь вид: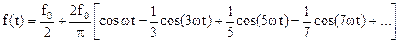 .
.
 ,
, ,
,  ,
, ,
, 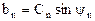 .
. , (ватт)
, (ватт) ,
, , (ватт/Гц)
, (ватт/Гц)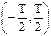 – интервал длительности сигнала.
– интервал длительности сигнала.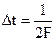 . Общее число таких отсчетов для сигнала длительностью Т равно
. Общее число таких отсчетов для сигнала длительностью Т равно  (где n – число членов разложения, т.е. отсчетов функции f(t)).
(где n – число членов разложения, т.е. отсчетов функции f(t)). ,
, – функция отсчета;
– функция отсчета; – интервал дискретизации.
– интервал дискретизации. .
. , что позволяет любой непрерывный сигнал f(t) представить в виде импульсной последовательности. Поэтому ортогональные разложения Котельникова являются теоретической основой методов дискретной передачи непрерывных сообщений.
, что позволяет любой непрерывный сигнал f(t) представить в виде импульсной последовательности. Поэтому ортогональные разложения Котельникова являются теоретической основой методов дискретной передачи непрерывных сообщений.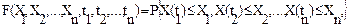 ,
,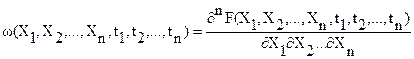
 ,
, – является функцией времени.
– является функцией времени. называется центрированным процессом:
называется центрированным процессом: .
.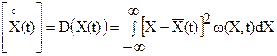 ,
,
 .
. .
. .
. и
и  не зависят от времени, но являются случайными величинами, зависящими от i-ой реализации и длительности интервала Т наблюдения случайного процесса.
не зависят от времени, но являются случайными величинами, зависящими от i-ой реализации и длительности интервала Т наблюдения случайного процесса.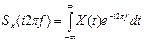 .
.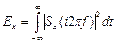 ,
, характеризует распределение энергии реализации случайного процесса по оси частот f. Это спектральная плотность энергии реализации.
характеризует распределение энергии реализации случайного процесса по оси частот f. Это спектральная плотность энергии реализации. .
. ,
, ,
,


