Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление аналоговых сигналов в дискретном времени. Цифровые методы модуляции сигналов. Структура и принципы функционирования аналого-цифровых и цифро-аналоговых преобразователей. Вокодеры ⇐ ПредыдущаяСтр 3 из 3
Современные системы связи характеризуются все более широким внедрением цифровых методов передачи информации. В таких системах подлежащее передаче сообщение состоит из последовательности дискретных символов, выбираемых из конечного алфавита. Такое представление вполне естественно для сообщений типа письменного текста, цифровых данных или машинного кода. Если же исходное сообщение является речью, музыкой и изображением (т.е. сигналом непрерывным по времени и по амплитуде), то к нему необходимо применить процесс дискретизации (преобразование из непрерывного времени в дискретное) и квантования (заменить непрерывный диапазон амплитуд конечным рядом дискретных уровней). Такое представление имеет следующие преимущества: Слабое влияние неидеальности характеристик и их нестабильности в аппаратуре связи на качество передачи информации. Возможность манипуляции с дискретной информацией с целью использования кодов, исправляющих и корректирующих ошибки засекречивания информации и ее уплотнение, откуда следует высокая помехоустойчивость даже при наличии большого уровня шумов и помех. Возможность восстановления формы сигналов в трансляторах сети связи, благодаря чему ошибки и шумы не накапливаются при передаче сигналов на большие расстояния. Универсальная форма представления различных сообщений (речь, телеизображение, дискретные данные и т.д.) и следовательно возможность унификации аппаратуры связи. Низкая чувствительность к нелинейным искажениям, что дает возможность передачи информации по групповым трактам многоканальных систем. Простое согласование с ЭВМ и электронными автоматическими телефонными станциями, что дает возможность создавать интегральные сети связи с возможностью автоматизации процедур передачи и обработки информации с помощью ЭВМ. Дискретизация непрерывных сигналов во времени осуществляется на базе Теоремы отсчетов. На рисунке1.14. показан непрерывный сигнал x(t) с ограниченным спектром, т.е. S(f) = 0 при |f|>w.
Рис. 1.14.
Тогда согласно этой теореме шаг дискретизации Dt выбирается из соотношения Как видно из рисунка 1.15, отсчеты, взятые в моменты времени tk = kDt полностью определяют сигнал x(t) (если длительность сигнала Т то k = 2wT, т.е. число отсчетов)

Рис. 1.15.
Далее осуществляется квантование сигнала по уровню. Смысл этой процедуры заключается в том, что выбирается конечное число уровней квантования (например от –4 до +4 с равным шагом DU=1, т.е. 8 уровней) и каждое истинное значение высоты (амплитуды) отсчета заменяется ближайшим целым числом от –4 до +4. На рисунке 1.16 показан результат квантования.
Рис. 1.16.
Как видно процесс квантования сигнала по уровню вносит ошибку квантования, и восстановленный сигнал
Если квантование выполняют с равномерным шагом DU, то область изменения мгновенных значений шума квантования (абсолютная погрешность квантования) e(t) заключена в пределах от
Дисперсию называют мощностью шумов квантования. Она падает с ростом числа уровней квантования и при правильном выборе этого числа может стать пренебрежительно мала, по сравнению с мощностью помех. Например 32 уровня считается достаточным для качественной передачи речевых сигналов. На практике в ряде случаев равномерное квантование не применяют, особенно в тех случаях, когда динамический диапазон передаваемых сигналов различен. В этих случаях для уменьшения погрешности квантования сжимают динамический диапазон полезных сигналов. Такое сжатие называют компрессированием динамического диапазона сигнала и связано оно с уменьшением интервала квантования полезного сигнала и, следовательно, с уменьшением мощности шумов квантования. Такое компрессирование можно делать перед квантованием и затем использовать равномерное квантование полезного сигнала. После декодирования и восстановления сигнала выполняется обратная операция, называемая экспандированием. Обе эти операции называют компандированием сигнала. Таким образом, влияние шумов квантования и помех можно уменьшить, оптимально выбирая параметры квантования и искусственно изменяя динамический диапазон полезных сигналов (компандирование).
Цифровые методы передачи информации по каналам связи основаны на следующих основных преобразованиях: дискретизации, квантовании (рассмотрены выше), кодировании (рассмотрим в дальнейшем) и модуляции. Рассмотрим цифровую модуляцию. Ее сущность заключается в следующем: передаваемый непрерывный сигнал квантуется по времени и уровням; полученные после этого отсчеты сигнала в дискретные моменты времени рассматриваются как числа в той или иной системе счисления, которые затем кодируются для преобразования их в кодовые комбинации электрических сигналов. Полученной кодовой последовательносью сигналов аналоговым или дискретным способом модулируется высокочастотный сигнал-переносчик. Последнее преобразование выполняется, как правило, для многоканальных систем. В остальных случаях выполняют операции квантования, дискретизации и кодирования. Наибольшее применение на практике получили такие цифровые методы модуляции как импульсно-кодовая модуляция (ИКМ) и дельта-модуляция (ДМ). На рисунке 1.17 показаны временные диаграммы сигналов для ИКМ.
Рис. 1.17.
Здесь B(t) непрерывный сигнал, который ИК модуляцией преобразуется в кодовую последовательность U(t). Интервал отсчетов выбирается по Теореме отсчетов, т.е. Более простой по сравнению с ИКМ является дельта-модуляция. Сущность этого метода заключается в том, что в каждый дискретный момент времени tk взятия отсчета передается положительный импульс постоянной амплитуды и длительности, если производная сигнала в этой точке положительна, и отрицательный импульс, если производная отрицательна.
Рис. 1.18.
В результате кодирования в дельта-модуляторе исходное сообщение B(t) в виде непрерывного сигнала преобразуется в последовательность положительных и отрицательных импульсов. Для преобразования непрерывных сигналов в цифровой код и наоборот в системах связи используют специальные устройства аналого-цифровой (АЦП) и цифро-аналоговый (ЦАП) преобразователи. По сути дела АЦП осуществляет ИКМ, т.е. выполняет следующие операции: дискретизацию непрерывного сигнала по времени, квантование по уровню и полученная последовательность квантованных значений путем кодирования представляется в виде последовательности m-ичных кодовых комбинаций (чисел). Чаще всего кодирование здесь используется двоичное, т.е. делается запись номера уровня квантования в двоичном коде. Рассмотрим принципы функционирования аналого-цифровых и цифро-аналоговых преобразователей. Структурная схема АЦП может быть представлена в виде, показанном на рисунке 1.19.
Рис.1.19.
Принцип его работы заключается в следующем: сначала непрерывное сообщение B(t) подвергается дискретизации по времени через интервалы Dt; полученные отсчеты B(tk) квантуются по уровням Bкв(tk); каждое квантованное значение Bкв(tk) в момент времени tk = Dtkk кодируется соответствующим двоичным числом BИКМ(tk). Функциональная схема АЦП представлена на рисунке 1.20
Рис. 1.20.
где Uвх – входной аналоговый сигнал; U0 – опорное напряжение; Кj – компаратор (сравнение); Тр – триггер; К – преобразователь в двоичный код; fт – тактовая частота, задающая частоту дискретизации. Входной аналоговый сигнал Uвх поступает на все компараторы К1, К2, …, К15 и сравнивается с опорным напряжением U0, которое делителем на базе резисторов R делится на 2n уровней квантования. Каждый i-й компаратор выдает сигнал "0" если входной сигнал Uвх < U0i опорного напряжения на этом компараторе и сигнал "1", если входной сигнал достигает U0i. Например, опорные напряжения имеют значения для К1 U01=1, для К2 U02=2, …, для К15 U015=15. На вход подается Uвх=12, значит компараторы К1, …, К12 перейдут в состояние "1", а К13=К14=К15=0. Этот двоичный код записывается в триггеры и затем преобразуется в преобразователе К в код из 4-х разрядов. (Для 16 уровней квантования достаточно 4-х разрядного двоичного кода, т.к. 24=16). Теперь рассмотрим параллельный 4-х разрядный ЦАП, показанный на рисунке 1.21.
Числовое значение кодовых посылок
Например, если код 1010, то
Рассмотренные выше методы преобразования аналоговых сигналов предназначены для воспроизведения формы этих сигналов с максимальной точностью. Эти методы не учитывают априорных данных о сигнале и по существу применимы для любых непрерывных сигналов. Рассмотрим теперь специальную группу устройств преобразования непрерывных сигналов в цифровую форму. Эти устройства проблемно ориентированы на преобразование только речевых непрерывных сигналов и получили название вокодеры (кодеры речевых сигналов). Способы преобразования речевых сигналов в цифровую форму, используемые в вокодерах, весьма специфичны и поэтому не используются в телефонных сетях общего назначения, где наряду с речевыми сигналами должна быть обеспечена передача и других аналоговых сигналов. Кроме того, вокодеры обычно создают ненатуральное или синтетическое звучание речи. Основным назначением вокодеров является кодирование только важных для восприятия параметров речи с уменьшенным числом символов по сравнению с их общим числом, которые обеспечивают требуемый уровень качества восприятия речи. Поэтому вокодеры могут быть использованы для передачи речи в ограниченной полосе, чего не могут обеспечить другие средства. Основным их применением является: передача сигналов типа "неправильно набран номер", передача секретных сигналов, формирование речевого сигнала на выходе ЭВМ и другие.
№Кодирование информации в системах связи. Принципы помехоустойчивого кодирования информации. Классификация помехоустойчивых кодов. Помехоустойчивые коды Хэмминга и циклические коды. Структуры кодеров и декодеров
Как уже указывалось выше использование цифровых методов передачи сообщений и сигналов дает целый ряд преимуществ системам связи. Одним из таки преимуществ является возможность использования помехоустойчивого кодирования сигналов на основе использования специальных кодов для повышения верности передачи информации.
Коды источников сообщений
Напомним, что источник сообщения формирует сообщение А(t) (которое может быть любой физической природы – звуковые колебания, изображения и т.д.), которое преобразователем (кодером источника) преобразуется в первичный код B(t). Поскольку сейчас мы рассматриваем цифровые методы передачи информации, будем считать, что этот первичный сигнал B(t) формируется в кодере источника (одним из рассмотренных ранее методов цифровой модуляции, например ИКМ) в виде последовательности цифровых кодовых комбинаций, каждая из которых содержит m разрядов или m единичных элементов. Иными словами каждая кодовая комбинация характеризуется основанием кода К и числом единичных элементов m. В технике передачи дискретных сообщений наибольшее распространение получили двоичные коды с основанием К=2. Поэтому в дальнейшем будем полагать, что кодовые комбинации, отображающие исходное сообщение, представляют собой m-разрядные двоичные коды. Длительность передачи одного единичного элемента кодовой комбинации (в данном случае 0 или 1) называют единичным интервалом t0. Тогда скорость передачи единичных элементов измеряется как:
Первичные коды сообщений можно разделить на две группы: неравномерные и равномерные. Неравномерные коды характеризуются тем, что кодовые комбинации состоят из различного числа m единичных элементов. Примером такого кода является телеграфный код Морзе, где точка –это 1, тире – 111, 0 – разделяет точки и тире, 000 – разделяет кодовые комбинации (буквы, цифры). При таком кодировании длительность кодовой комбинации, соответствующей букве Е = 4t0, а букве Т = 6t0, а цифре 0 - 22t0. Неравномерность кода затрудняет при его применении различие между кодовыми комбинациями, т.к. приемник не только должен отличать единичные элементы 0 от 1, но и реагировать на длительность кодовой комбинации. Поэтому на практике в основном используют равномерные коды с постоянным числом m единичных элементов во всех кодовых комбинациях. Общее число m-элементных кодовых комбинаций двоичного равномерного кода равно К = 2m.
Примером такого кода является стандартный 5-элементный телеграфный код МТК-2, принятый в качестве международного стандарта и представленный в таблице 1.1.
Таблица 1.1.
Здесь для сокращения числа разрядов и увеличения скорости передачи одни и те же кодовые комбинации используются для передачи букв и цифр. В приемнике при помощи несложного устройства-регистра печатается тот или другой знак в зависимости от передаваемого текста. Это осуществляется передачей соответствующих управляющих сигналов – перевод на русский, возврат каретки, перевод строки и т.д. Развитие техники передачи данных и внедрение ЭВМ привели к появлению телеграфных кодов с расширенным набором команд. Поэтому существует еще стандартный телеграфный 7-элементный код КОИ-7, разработанный на основе рекомендованного МККТТ Международного кода №5 (МККТТ – международный консультативный комитет по телеграфии и телефонии). Таким образом, в качестве первичных кодов B(t) будем в дальнейшем рассматривать равномерные двоичные коды с числом разрядов m. Для повышения верности передачи таких кодов по каналам связи используется дополнительное их преобразование в кодере источника, называемое помехоустойчивым кодированием.
Помехоустойчивое кодирование
Сущность помехоустойчивого кодирования заключается во введении в первичные коды B(t) избыточности. Поэтому помехоустойчивые коды называют избыточными. Задача помехоустойчивого кодирования заключается в таком добавлении к информационным символам первичных кодов дополнительных символов, чтобы в приемнике информации могли быть найдены и исправлены ошибки, возникающие под действием помех при передаче кодов по каналам связи.
Классификация помехоустойчивых кодов
Существует множество различных способов введения избыточности в коды. Избыточные коды делятся на блочные и непрерывные. В блочных кодах передаваемая информация разбивается на отдельные блоки – кодовые комбинации, которые кодируются и декодируются независимо. Если число элементов первичного кода равно m, а вводимых дополнительных проверочных элементов кода равно r, то общее число элементов в кодовой комбинации блочного избыточного кода равно n = r + m. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определенном порядке между информационными. На практике чаще всего используются блочные коды. Блочные коды делятся на разделимые и неразделимые. В разделимых кодах информационные и проверочные элементы во всех кодовых комбинациях занимают одни и те же позиции. Поэтому разделимые коды обозначают (n, m) коды. В неразделимых кодах деление на информационные и проверочные элементы отсутствует. Разделимые коды делятся на линейные и нелинейные. Первые названы так потому, что их проверочные элементы представляют собой линейные комбинации информационных элементов. Большую и важную группу линейных кодов образуют циклические коды. Нелинейные коды характеризуются наличием 2-х и более проверок внутри каждой кодовой комбинации.
Обнаружение и исправление ошибок
Наличие в кодовых комбинациях заведомо большего числа единичных элементов n>m, чем это минимально необходимо для первичного кодирования, приводит к тому, что из общего числа N=2n кодовых комбинаций (n, m) только Np=2m разрешены, а остальные (N-Np) являются запрещенными и для кодирования сообщений не используются. Избыточность помехоустойчивых кодов оценивается коэффициентом избыточности
По своим корректирующим свойствам избыточные коды делятся на коды, обнаруживающие ошибки, исправляющие ошибки и частично обнаруживающие и исправляющие ошибки. Очевидно, что чем больше избыточность кода, тем лучше его корректирующие свойства. Это объясняется тем, что чем больше r и значит n при заданном m, тем легче из общего числа кодовых комбинаций N выбрать Np разрешенных кодовых комбинаций, заметно отличающихся друг от друга. Степень отличия кодовых комбинаций характеризуется кодовым расстоянием d, которое определяется как число позиций единичных элементов, которым одна кодовая комбинация отличается от другой. Например, кодовое расстояние d между комбинациями 100001 и 011000 будет равно d=4. Весом V кодовой комбинации является количество входящих в нее единиц. Вес комбинации 100001 равен V=2, а вес комбинации 011000 равен V=2.
С другой стороны сумма этих комбинаций по модулю 2 дает суммарную комбинацию 111001, вес которой V=4 и равен кодовому расстоянию между комбинациями-слагаемыми 100001 и 011000 Корректирующие свойства кода определяются минимальным кодовым расстоянием d0 (расстояние Хэмминга) между любыми двумя кодовыми комбинациями. Так, например, для первичного кода МТК-2, все кодовые комбинации разрешены и расстояние Хэмминга d0 = 1. Это означает, что искажение хотя бы одного единичного элемента любой кодовой комбинации кода МКТ-2, приводит к замене этой кодовой комбинации на другую, т.е. ошибки не могут быть обнаружены. Для обнаружения ошибок необходимо, чтобы d0 ³ t0 + 1, где t0 – кратность обнаруживаемых кодом ошибок. Для исправления ошибок необходимо, чтобы расстояние от принимаемой с ошибками запрещенной комбинации до переданной комбинации было меньше, чем до любой другой разрешенной комбинации. Другими словами необходимо, чтобы кратность ошибки не превышала половины кодового расстояния d0 ³ 2tu + 1, где tu – кратность исправляемых ошибок. Определяемые из указанных выражений значения t0 и tu дают число гарантированно обнаруживаемых и исправляемых ошибок. Из этих выражений также следует, что коды, исправляющие ошибки, можно использовать для гарантированного обнаружения ошибок кратностью t0=2tu. Чтобы код обнаруживал ошибки кратностью t0 и исправлял ошибки кратностью tu кодовое расстояние должно быть d0 ³ t0 + tu + 1.
Простейшие помехоустойчивые коды
Введение в коды избыточности можно осуществлять по различным правилам. Одним и наиболее часто используемым правилом является правило проверки на четность числа единиц в кодовой комбинации (разрешенной). Комбинации этого кода образуются путем добавления к m информационным элементам (битам в случае двоичного кода) одного проверочного (m+1) бита, так чтобы полное число единиц в кодовой комбинации было четным. Если А = {a1, …, am} единичные элементы первичного кода, а В – проверочный элемент, то для обеспечения четного числа единиц необходимо, чтобы b = a1 Å a2 Å … Å am, или a1 Å a2 Å … Å am Å b = 0, где Å – сумма по модулю два. Например для m=4 код с проверкой на четность будет иметь вид:
Такой код имеет d0=2 и значит, он не может исправить ни одной ошибки. Такой код может обнаружить одну ошибку. К простейшим помехоустойчивым линейным блочным кодам относится также код Хэмминга, позволяющий исправить одну ошибку и имеющий d0=3. Этот код строится следующим образом (для примера рассмотрим код (7,4)). К 4-м информационным битам а1а2а3а4 добавляем три проверочных бита b1b2b3, задавая их равенствами вида: a1 Å a2 Å a3 = b1, a2 Å a3 Å a4 = b2, a1 Å a2 Å a4 = b3. (при формировании этих правил каждый информационный элемент аi (i=1,2,3,4) должен участвовать как минимум в (r-1) проверках на четность из общего их числа r). Если будут выполняться эти правила, то это будет свидетельствовать об отсутствии ошибки. Невыполнение первого и третьего равенства свидетельствует об ошибочном приёме а1, первого и второго - об ошибке а3,первого, второго и третьего - об ошибке а2, второго и третьего - об ошибке а4. Представленное выше правило формирования проверочных элементов b1b2b3 кода Хэмминга позволяет путём проверки на чётность каждой кодовой комбинации определить порядковый номер искажённого элемента. Результат проверки на чётность удобно представить r=3 разрядным проверочным двоичным числом, называемым синдромом ошибки (S1,S2,S3): s1 = a1 Å a2 Å a3 Å b1, s2 = a2 Å a3 Å a4 Å b2, s3 = a1 Å a2 Å a4 Å b3. Имеется всего восемь возможных синдромов ошибки: один – для случая отсутствия ошибки s=(0,0,0) и семь для каждой из ошибок (по числу позиций кода n=7). Каждая из ошибок имеет свой единственный синдром. По этому синдрому можно обнаружить ошибку и указать ее позицию: s1s2s3: 000, 001, 010, 011, 100, 101, 110, 111. Пример: Первичный код а = (а1а2а3а4) = 0001, тогда b1 = a1 Å a2 Å a3 = 0, b2 = a2 Å a3 Å a4 = 1, b3 = a1 Å a2 Å a4 = 1.
Отсюда код Хэмминга а1а2а3а4b1b2b3 = 0001011.
Этот код передается по каналу и происходит искажение одного (пусть а2 символа).
Вычисляем синдром s= s1s2s3.
Синдромом 111 можно закодировать ошибку а2. Нетрудно видеть, что если код Хэмминга принят правильно, то синдром s=000, т.е. отсутствуют ошибки. Если бы ошибка была в а4, то синдром s=011. Схемная реализация кодеров и декодеров линейного блочного кода Хэмминга показана на рисунке 1.22.
Основной задачей при построении линейных блочных кодов как и любых других помехоустойчивых кодов является разработка правил формирования проверочных элементов. Напомним, что эти правила заключаются в том, чтобы в результате проверок на четность числа единиц в передаваемой кодовой комбинации можно было указать позиции (номера) искаженных элементов. Последовательность кодовых комбинаций первичного m разрядного кода сообщения можно записать в виде матрицы
Чтобы не записывать все кодовые комбинации этой матрицы можно записать единичную матрицу размером m´m.
а все кодовые комбинации матрицы А получить путем поэлементного сложения по модулю 2 строк единичной матрицы I во всех возможных сочетаниях. Общее число таких сложений
Вообще Np = 2m и уменьшение на единицу связано с отсутствием комбинации 000…0. Для задания избыточного кода необходимо построить образующую матрицу Mn,m, левая часть которой есть единичная матрица Im первичного кода, а правая Rr,m – матрица проверочных элементов. Размерность такой матрицы n´m.
Теперь на основе образующей матрицы М можно построить проверочную матрицу Н размерностью n´r, левая часть которой это транспонированная матрица проверочных элементов, а правая – единичная матрица
Единицы в строках матрицы Н будут стоять на позициях элементов, участвующих в проверке на четность при формировании соответствующих bi (i = 1, 2, …, r). Таким образом, если задана образующая матрица М, то построив по ней проверочную матрицу, можно найти правила формирования проверочных групп элементов. Такой матричных подход удобен при построении линейных блочных кодов с большим числом разрядов m и r.
Циклические коды
Циклические коды – это разновидность линейных блочных кодов и предназначены они для обнаружения и исправления ошибок. Любое m разрядное число можно представить в виде многочлена F(x) = am-1xm-1 + am-2xm-2 + … + a1x1 + a0x0. Здесь коэффициенты a1, a2, …, am-1 равны "0" или "1". Для двоичных кодов это будет иметь вид F(x) = am-12m-1 + am-22m-2 + … + a121 + a020. Например, кодовую комбинацию 1111 можно записать F1 = x3 + x2 + x + 1, а для 1001 F2 = x3 + 1. Такое представление двоичных чисел более компактно. Над многочленами можно производить любые алгебраические операции (умножение, деление и т.д.) за исключением сложения и вычитания, которые заменяются на суммирование по модулю два. F1(x) Å F2(t) = x2 + x. В основе построения циклических кодов лежит представление их в виде указанных многочленов. Широкое применение таких кодов обусловлено их способностью обнаруживать и исправлять ошибки различной конфигурации, удобством математического аппарата для их описания и простотой технической реализации кодеров и декодеров. Построение циклических кодов основано на представлении первичного кода в виде многочлена степени m-1 f(x) и представления в виде многочлена степени r-1 r(x) проверочного кода. Тогда многочлен циклического кода равен F(x) = f(x)xr + r(x). Умножение f(x) на xr необходимо, чтобы сдвинуть информационные элементы на r разрядов влево и тем самым освободить справа r разрядов для записи r проверочных элементов. Построенный таким образом многочлен F(x) должен делиться без остатка на образующий многочлен M(x) степени r, т.е.
или с учетом правил двоичной алгебры
Отсюда видно, что многочлен проверочных элементов r(x) является остатком от деления f(x)xr на М(х). Так как максимальная степень остатка всегда по крайней мере на единицу меньше степени делителя, становится ясно, почему степень образующего многочлена выбирается равной r. Пример: пусть задана m=5 пятиэлементная комбинация первичного кода 10000 = f(x) = x4. Требуется построить циклический код, имея в виду возможность исправления однократных ошибок (т.е. d0=3). Этому условию удовлетворяет r=4. Возьмем в качестве образующего многочлена М(х)=х4+х+1 и разделим
Тогда циклический код F(x)=f(x)xr+r(x)=100000101. При приеме комбинации циклического кода f(x) ее принадлежность к разрешенной или запрещенной определяется отсутствием или наличием остатка от ее деления на образующий многочлен М(х). Для исправления ошибок нужно, чтобы остатки от деления, т.е. r(x) служили синдромами ошибки. То есть каждому варианту ошибки должен соответствовать свой остаток. Для этого необходимо правильно выбрать образующий многочлен М(х). Обычно в качестве М(х) выбирают неприводимые многочлены, которые могут быть представлены в виде произведения многочленов низших степеней. Пример таких многочленов показан в таблице 1.2. Таблица 1.2.
Однако не всегда неприводимый многочлен сможет служить в качестве образующего многочлена. Это можно продемонстрировать на примере. Рассмотрим пример построения циклического кода (9,5) для комбинации первичного кода х4=10000=f(x). Число проверочных элементов r=4 при d0=3. Следовательно образующий многочлен М(х) имеет степень r=4. Для r=4 из таблицы имеются три неприводимых многочлена. Построим для каждого из них циклический код.
F(x) = f(x) xr + r(x) = 100000101 – циклический код.
F(x) = 100001110.
F(x) = 100001000. Как видно для примера 1 вес кодовой комбинации V1 = 3 = d0, для 2 – V2 = 4 > d0, а для 3 – V3 = 2 < d0. Это значит, что третий неприводимый многочлен М3(х) не может быть использован в качестве образующего для циклического кода, исправляющего одиночные ошибки (d0=3).
Кодеры и декодеры циклических кодов
Для построения кодирующего устройства циклического кода необходимо иметь схему, вычисляющую остаток r(x) от деления f(x)xr на образующий многочлен М(х). Такую схему легко получить на регистре сдвига с обратными связями и сумматорах по модулю два. Деление f(x)xr на М(х) сводится к сложению по модулю два числа, соответствующего многочлену делителя, т.е. М(х), сначала со старшими разрядами делимого, т.е. f(x)xr, а затем с промежуточными остатками. Это может быть сделано на основе регистра сдвига, число ячеек которого равно степени образующего многочлена М(х), а в цепях обратных связей стоят сумматоры по модулю два, число и место которых определяется ненулевыми коэффициентами образующего многочлена М(х). Например: кодирующее устройство (7,4) кода по образующему многочлену (r=3) М(х) = х3 + х + 1 имеет вид, показанный на рисунке 1.23.
Рис.1.23.
Правила заполнения ячеек регистра: если на входе ячейки стоит сумматор по модулю два (ячейки 0 и 1), результат записывается как сумма по модулю два сигнала из соседней ячейки (предшествующей) и сигнала обратной связи в данном такте. Пусть f(x) = х3 = 1000. Этот сигнал последовательно старшими разрядами поступает в ячейки регистра и одновременно появляется на выходе через схему ИЛИ (ключ в положении 1). В результате за первые m=4 тактов на выходе появится f(x), а в регистре сформируется остаток r(x) от деления f(x)xr на М(х). Тогда ключ переводится в положение 2 и на выходе появляется остаток r(x). То есть за m+r тактов на выходе формируется циклический код F(x) первичного кода f(x), как показано в таблице 1.3. Таблица 1.3.
Декодер циклического кода (7,4) показан на рисунке 1.24.
Рис.1.24.
Здесь код тоже подается старшими разрядами вперед, F(x) – циклический код, делится на образующий многочлен. Это схема декодера для циклического кода (7,4) с образующим многочленом М(х) = х3 + х + 1 (как и для кодера, рассмотренного выше). Остаток r(x) – это синдром ошибки, дешифратор настроен на исправление ошибки при каждом виде синдрома как и в ранее рассмотренном коде Хэмминга. Наряду с рассмотренными выше в последнее время получили практическое применение сверточные коды и целый ряд других типов кодов. С ними вы можете при необходимости познакомиться в книге Р. Блейхута "Теория и практика кодов, контролирующих ошибки". –М.: "Мир", 1986 г.
1.7 Многоканальные системы передачи информации. Уплотнение информации в аналоговых системах связи. Частотное разделение сигналов. Временное разделение сигналов. Разделение сигналов по форме. Комбинационное разделение сигналов. Цифровые системы многоканальной передачи информации
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.213.209 (0.159 с.) |

 , чтобы можно было полностью восстановить сигнал на выходе канала связи.
, чтобы можно было полностью восстановить сигнал на выходе канала связи.
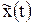 отличается от исходного сигнала x(t) на величину ошибки квантования e(t), т.е.
отличается от исходного сигнала x(t) на величину ошибки квантования e(t), т.е. .
. до
до  . На рисунке 1.16 показана абсолютная погрешность ε1, ε2, ε3, ε4, ε5, в моменты t1, t2,…t5. Обычно ошибку квантования считают равномерно распределенной в интервале
. На рисунке 1.16 показана абсолютная погрешность ε1, ε2, ε3, ε4, ε5, в моменты t1, t2,…t5. Обычно ошибку квантования считают равномерно распределенной в интервале  , поэтому математическое ожидание и дисперсия ошибки равны
, поэтому математическое ожидание и дисперсия ошибки равны ;
; .
.
 , где w – верхняя частота спектра B(t).
, где w – верхняя частота спектра B(t).



 Рис. 1.21.
Рис. 1.21. . При поступлении "1" ключ в положении 2, при следовании "0" – ключ в положении 1. Коэффициент передачи выходного усилителя Y равен 3/2. (Здесь а1 – старший разряд, аn – младший). Если в положении 2, т.е. а1=1 только переключатель первого разряда, то выходное напряжение будет равно
. При поступлении "1" ключ в положении 2, при следовании "0" – ключ в положении 1. Коэффициент передачи выходного усилителя Y равен 3/2. (Здесь а1 – старший разряд, аn – младший). Если в положении 2, т.е. а1=1 только переключатель первого разряда, то выходное напряжение будет равно  . При а2=1 и аi=0, то
. При а2=1 и аi=0, то 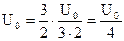 . Если поступает несколько единиц, то напряжения суммируются:
. Если поступает несколько единиц, то напряжения суммируются: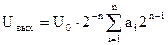 .
.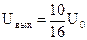 .
. с-1 (Бод).
с-1 (Бод). .
. .
. ,
,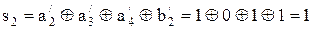 ,
, .
. Рис.1.22.
Рис.1.22. .
.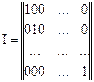
 .
.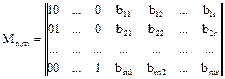 .
. .
. ,
, .
.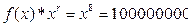 на
на