
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерительные системы статистических характеристик случайных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Данные системы предназначены для измерения вероятностных (статистических) характеристик случайных процессов. Под вероятностными характеристиками случайных процессов понимают математическое ожидание, дисперсию, законы распределения вероятностей, корреляционные и спектральные функции. Т. о., использование ПК и ИИС связано с вероятностными принципами представления измерительной информации. Под исследованием операций понимается применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности. Для выполнения любого мероприятия, в том числе и определённых измерений, существует определённая свобода выбора для достижения поставленной цели, то есть, конкретное измерение можно организовать тем или иным способом. При этом, полученное решение – это и есть определённый выбор из ряда возможностей, имеющихся у исследователя. Чем сложнее, дороже и масштабнее планируемое мероприятие, тем менее допустимы в нём «волевые» решения и тем важнее становятся научные методы, позволяющие заранее отбросить недопустимые варианты и рекомендовать наиболее рациональные, установить, достаточна ли имеющаяся информация для правильного принятия ЭТР, и если нет – какую информацию следует получить дополнительно. Случайное событие – всякий факт, который может произойти или не произойти в процессе испытаний. Более сложным понятием является группа событий. Существует понятие полная группа событий – это несколько событий, таких, что хотя бы одно из них непременно должно появиться в результате испытания. Если никакие два события из группы событий не могут появиться вместе, то эти события называются несовместимыми. Из всех событий выделяют элементарные события, соответствующие результатам испытаний с равновероятным положительным и отрицательным исходами. Результатом испытания может считаться принятие некоторой величиной одного из возможных значений. Такую величину называют случайной величиной, если выбор одного из результатов случаен. Часто на практике для определения результата испытаний необходимо рассматривать совместно (одновременно) совокупность двух или более случайных величин. Такая совокупность называется системой случайных величин. Если конкретные значения, принятые в результате испытаний каждой из случайных величин, задают значения координат в пространстве соответствующей размерности, то систему случайных величин называют случайный многомерный вектор. Если одна случайная величина Y является результатом определённого функционального преобразования другой случайной величины Х, то множество значений Y является функцией случайной величины Х. При этом, случайная величина может быть функцией многих случайных величин. Итак, случайной функцией (случайным процессом) называют функцию одного аргумента (чаще временного), которая принимает в результате испытания некоторый конкретный вид, называемый реализацией случайной функции (случайного процесса). Статистические модели, по сравнению с аналитическими, более точны и подробны, не требуют грубых допущений и позволяют учесть большое число факторов. Случайная величина – количественная характеристика случайного явления. Примерами случайных величин являются погрешности измерений, время безотказной работы технических систем и т. д. Случайные величины подразделяются на дискретные и непрерывные. Дискретная величина – принимает на любом конечном отрезке числовой прямой конечное число различных значений. Непрерывная величина – значения случайной величины целиком заполняют некоторые интервалы числовой прямой. Полной характеристикой случайной величины с вероятностной точки зрения является её закон распределения, то есть заданная в той или иной форме связь между её возможными значениями и их вероятностями появления. К наиболее распространённым законам распределения случайных величин относят: равномерный, нормальный (закон Гаусса), усечённый нормальный закон, экспоненциальный (показательный) и др. Основными простейшими характеристиками случайной функции являются математическое ожидание, дисперсия, среднее квадратическое отклонение и корреляционная функция. Вероятность события, очевидно, всегда есть положительное число или 0. она не может быть больше 1, потому что у дроби, которой она определяется, числитель не может быть больше знаменателя (число «удачных» операций не может быть больше числа всех предпринятых операций). Каково бы не было событие А, его вероятность Р(А) определяется из соотношения 0 £Р(А) £ 1, так как Чем больше Р(А), тем чаще наступает событие А. Если Р(А) = 0, то событие А считается невозможным. Если Р(А) = 1, то событие А считается практически достоверным. Математическое ожидание является числовой характеристикой случайной величины Х как среднее значение некоторой функции f(x) этой случайной величины, которое можно получить экспериментально и теоретически. Оно обозначается М(Х) и определяется из соотношения М(Х) = где n – число появлений значения Необходимо отметить, что класс дискретных величин недостаточен для описания реальных величин.действительно, таким величинам, как размеры любых физических объектов, температура, давление, длительность тех или иных физических процессов, совершенно неестественно приписывать дискретное множество возможных состояний. Их возможные значения могут быть любыми числами в некоторых пределах (н-р, длина всегда положительна). Поэтому используют формулы для непрерывных величин. М(Х) = где Значение М(Х) указывает центр промежутка возможных значений случайной величины, около которого распределяются (группируются) на числовой оси случайные точки. Если задано математическое ожидание, определяющееся формулой
Дисперсия случайной величины Х – это математическое ожидание квадрата отклонения случайной величины от математического ожидания М(Х). Дисперсия случайной величины Х определяется из соотношения
Рис.1. Структурная схема измерительной системы для измерения математического ожидания случайного процесса Если задана дисперсия, определяющаяся формулой
Рис.2. Структурная схема измерительной системы для измерения дисперсии случайного процесса Среднее квадратическое отклонение случайной величины Х – это число, равное квадратному корню от дисперсии.Среднее квадратическое отклонение случайной величины Х определяется из соотношения s(Х)= Значения sх и Dx характеризуют рассеивание случайных точек и их разбросанность относительно центра распределения Dx =s2х = М(Х2) – [M(X)]2. (7) Корреляционная функция Rx(t1,t2) случайной величины X(t) – это неслучайная функция двух аргументов t1 и t2, которая при каждом значении t равная корреляционному моменту двух соответствующих сечений
Корреляционный момент системы (X,Y) – это математическое ожидание произведения случайных величин
Для дискретных величин корреляционный момент определяется из соотношения
Для непрерывных величин корреляционный момент определяется из соотношения
Для стационарного эргодического процесса Х(t) корреляционная функция может быть определена как математическое ожидание центрированных значений в моменты времени t и t + t
Структурная схема, реализующая зависимость (12) представлена на рис. 3.
Рис. 3. Структурная схема измерительной системы для измерения корреляционной функции случайного процесса Взаимная корреляционная функция между двумя случайными процессами x(t) и y(t) определяется из соотношения
Структурная схема, реализующая зависимость (13) представлена на рис. 4.
Рис. 4.Структурная схема измерительной системы для измерения взаимной корреляционной функции между двумя случайными процессами
Спектр мощности характеризует частотное распределение случайного процесса, который определяется из соотношения
Структурная схема, реализующая зависимость (14) представлена на рис.5.
Рис. 5.Структурная схема измерительной системы для измерения спектра мощности случайного процесса
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

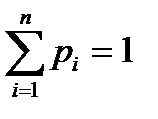 составляют полную группу событий. (1)
составляют полную группу событий. (1) - для дискретной величины, (2)
- для дискретной величины, (2) ;
;  - вероятность значения
- вероятность значения  - для непрерывной величины, (3)
- для непрерывной величины, (3) - функция случайной величины Х.
- функция случайной величины Х. , то эта статистическая характеристика может быть реализована с помощью структурной схемы, представленной на рис. 1.
, то эта статистическая характеристика может быть реализована с помощью структурной схемы, представленной на рис. 1.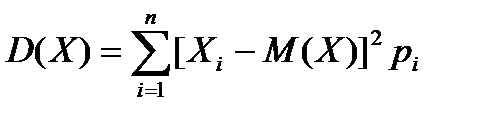 - для дискретной величины; (4)
- для дискретной величины; (4) - для непрерывной величины. (5)
- для непрерывной величины. (5)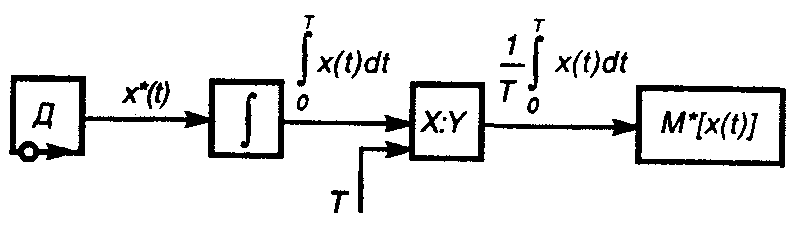
 , то эта статистическая характеристика может быть реализована структурной схемой, представленной на рис.2.
, то эта статистическая характеристика может быть реализована структурной схемой, представленной на рис.2.
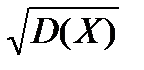 . (6)
. (6) . (8)
. (8) . (9)
. (9) . (10)
. (10)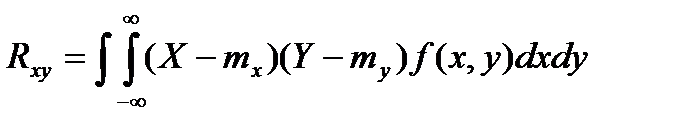 . (11)
. (11) . (12)
. (12)
 (13)
(13) .
. . (14)
. (14)



