
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема №9: работа сау при случайных воздействияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При действии на систему входного воздействия, которое представляет собой случайную функцию времени, на выходе САУ также будет случайная величина, т.е. будет тоже случайная функция времени. Рассмотренные ранее показатели качества не могут быть использованы для оценки поведения системы, к которой приложены такие воздействия. Наиболее правильным подходом к исследованию САУ, находящихся под влиянием случайных воздействий, является подход с позиций теории вероятностей. Известно, что случайные процессы подразделяются на стационарные и нестационарные. Если закон распределения не зависит от времени, то такой случайный процесс называется стационарным, в противном случае - нестационарным. Стационарные случайные процессы обладают свойством эргодичности, в соответствии с которой для стационарного случайного процесса с вероятностью, равной единице, всякое среднее по множеству равно соответствующему среднему по времени. В этом случае для определения статистических характеристик, вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой x(t), полученной при испытании одной системы в течение длительного времени. f(t) = mf(t) + f0(t). Соответственно выходная величина x(t) = mx(t) + x0(t). Для линейных систем на основании принципа суперпозиции каждая из составляющих находится порознь: mx(t) - как реакция на mf(t), а x0(t) - как реакция на f0(t). mx(t) = W(p) mf(t). Для стационарного случайного процесса mx(t) и mf(t) являются постоянными величинами. Поэтому на основании уравнения статики mx(t) = W(0) mf(t). (9.1) © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Для определения центрированных стационарных случайных величин f0(t) и x0(t) необходимо знать их либо корреляционные функции R(τ), либо спектральные плотности S(ω). Rx(τ) = M[x(t) x(t+τ)]. (9.2) Вследствие инерционности любой САУ случайный процесс не может изменяться бесконечно быстро, т.е. текущее значение случайной функции x(t) не является совершенно не зависимой величиной, а в какой-то степени в среднем зависит от предшествующего ее значения или, как говорят, коррелировано с ним. Корреляционная функция служит мерой этой зависимости. Она тем больше, чем меньше последующее значение данной случайной функции
Основные свойства корреляционной функции стационарного случайного процесса [2,12]: Rx(0) = M[x2] = Dx, (9.3) где [Dx] = в2 - дисперсия случайной величины.
при τ->
где Rfy(τ), Ryf(τ) - взаимные корреляционные функции. Они характеризуют взаимную связь двух случайных процессов между собой в моменты времени, отстоящие друг от друга на промежуток времени τ. При τ=0 будет Rfy(0) = Ryf(0). Для не связанных друг с другом случайных процессов очевидно Rfy(τ) = Ryf(τ) = 0.
среднее квадратическое отклонение
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Спектральная плотность S(ω) стационарного случайного процесса x(t) - это частотная функция, характеризующая спектральный (частотный) состав процесса, и представляет собой частотную характеристику для средних значений квадратов амплитуд гармоник, на которые может быть разложен случайный процесс. Спектральная плотность представляет собой двустороннее преобразование Фурье от корреляционной функции и имеет размерность [S(ω)]=в2/гц=в2с
Чтобы определить корреляционную функцию Rx(τ) по известной спектральной плотности Sx(ω) используется обратное преобразование Фурье
Для τ=0 имеем
По своему физическому смыслу спектральная плотность есть величина, которая пропорциональна средней мощности процесса в интервале частот от ω до +dω. На рис.9.2 изображены характеристики R(τ) и S(ω) для различных случайных процессов.
Кривые 4 на рис.9.2. соответствуют чисто случайному процессу, когда связь между последующими значениями x(t) совсем отсутствует. Такой случайный процесс называется белым шумом, т.е. при τ
где w(t) - весовая или импульсная функция замкнутой системы по входному воздействию f(t); τ1 - вспомогательное время интегрирования.
где τ2 - вспомогательное время интегрирования.Тогда корреляционная функция выходной величины
Учитывая формулы (9.8) и (9.9) корреляционная функция
Подставляя это выражение для определения корреляционной функции выходной величины (9.13) и поменяв порядок интегрирования, получим
Так как
Из приведенных выше выражений можно получить связь между спектральными плотностями входной и выходной величинами САУ при случайных стационарных процессах
где W(jω) - частотная передаточная функция системы. © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |









 имеем
имеем 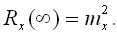 (9.4)
(9.4)  , (9.5)
, (9.5) (9.6)
(9.6) (9.7)
(9.7) . (9.8)
. (9.8) . (9.9)
. (9.9)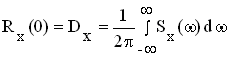 . (9.10)
. (9.10)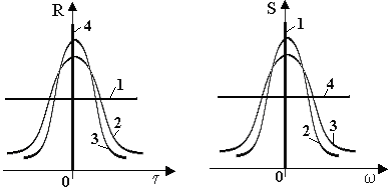
 0 Rx(τ) = 0, а S(ω) =const.
0 Rx(τ) = 0, а S(ω) =const. (9.11)
(9.11) (9.12)
(9.12) (9.13)
(9.13) (9.14)
(9.14)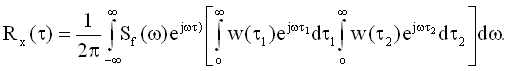


 (9.15)
(9.15) (9.16)
(9.16) (9.17)
(9.17)


