Тема №6: синтез линейных сау
Похожие статьи вашей тематики
Задача коррекции состоит в повышении точности систем как в установившихся режимах, так и в переходных. Она возникает тогда, когда стремление уменьшить ошибки управления в типовых режимах приводит к необходимости использования таких значений коэффициента усиления разомкнутой САУ, при которых без принятия специальных мер (установки дополнительных звеньев - корректирующих устройств) система оказывается неустойчивой.
| Типы корректирующих устройств
|  
|  
|  
| Различают три вида основных корректирующих устройств (Рис.6.1): последовательные (Wк1(p)), в виде местной обратной связи (Wк2(p)) и параллельные (Wк3(p)).
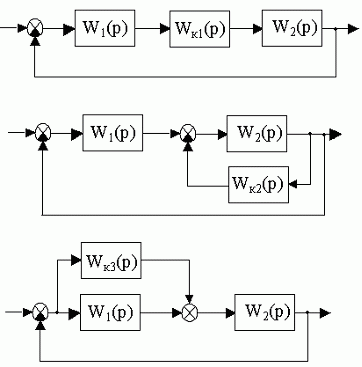
Рис.6.1. Структурные схемы корректирующих устройств.
Способ коррекции с помощью последовательных корректирующих устройств прост в расчетах и легко технически реализуется. Поэтому он нашел широкое применение, особенно при коррекции систем, в которых используются электрические цепи с немодулированным сигналом. Последовательные корректирующие устройства рекомендуется применять в системах, в которых нет дрейфа параметров звеньев. В противном случае требуется подстройка параметров коррекции.
Коррекция систем управления с помощью параллельного корректирующего устройства эффективна, когда имеется необходимость высокочастотного шунтирования инерционных звеньев. В этом случае формируются достаточно сложные законы управления с введением производных и интегралов от сигнала ошибки со всеми вытекающими из этого недостатками.
Коррекция местной (локальной) обратной связью используется в системах автоматического управления наиболее часто. Достоинством коррекции в виде местной обратной связи является существенно ослабление влияния нелинейностей характеристик звеньев, входящих в местный контур, а также снижение зависимости параметров настройки регуляторов от дрейфа параметров устройств.
Использование того или иного вида корректирующих устройств, т.е. последовательных звеньев, параллельных звеньев или обратных связей, определяется удобством технической реализации. В этом случае передаточная функция разомкнутой системы должна быть одной и той же при различном включении корректирующих звеньев:
 (6.1) (6.1)
Приведенная формула (6.1) позволяет произвести пересчет одного типа коррекции на другой, чтобы выбрать наиболее простой и легко реализуемый.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного
Синтез системы - это направленный расчет, целью которого является: построение рациональной структуры системы; нахождение оптимальных величин параметров отдельных звеньев. При множестве возможных решений первоначально необходимо сформулировать технические требования к системе. А при условии накладываемых на САУ определенных ограничений необходимо выбрать критерий оптимизации - статическая и динамическая точность, быстродействие, надежность, затраты энергии, цена и т.д.
При инженерном синтезе ставятся задачи: достижение требуемой точности; обеспечение определенного характера переходных процессов. В этом случае синтез сводится к определению вида и параметров корректирующих средств, которые необходимо добавить к неизменяемой части системы, чтобы обеспечить показатели качества не хуже заданных.
Наибольшее распространение в инженерной практике получил частотный метод синтеза с помощью логарифмических частотных характеристик.
Процесс синтеза системы управления включает в себя следующие операции:
- построение располагаемой ЛАЧХ L0(ω) исходной системы W0(ω), состоящей из регулируемого объекта без регулятора и без корректирующего устройства;
- построение низкочастотной части желаемой ЛАЧХ на основе предъявляемых требований точности (астатизма);
- построение среднечастотного участка желаемой ЛАЧХ, обеспечивающего заданное перерегулирование и время регулирования tп САУ;
- согласование низко- со среднечастотным участком желаемой л.а.х. при условии получения наиболее простого корректирующего устройства;
- уточнение высокочастотной части желаемой л.а.х. на основе требований к обеспечению необходимого запаса устойчивости;
- определение вида и параметров последовательного корректирующего устройства Lку(ω) = Lж(ω) - L0(ω), т.к. Wж(р) = Wку(р)*W0(р);
- техническая реализация корректирующих устройств. В случае необходимости проводится перерасчет на эквивалентные параллельное звено или ОС;
- поверочный расчет и построение переходного процесса.
Построение желаемой л.а.х. производится по частям.
Низкочастотная часть желаемой л.а.х. формируется из условия обеспечения требуемой точности работы системы управления в установившемся режиме, то есть из условия того, что установившаяся ошибка системы Δ( ) не должна превышать заданное значение Δ( ) не должна превышать заданное значение Δ( )≤Δз. )≤Δз.
Формирование запретной низкочастотной области для желаемой л.а.х. возможно разными способами. Например, при подаче на вход синусоидального сигнала требуется обеспечить следующие допустимые показатели: Δm - максимальная амплитуда ошибки; vm - максимальную скорость слежения; εm - максимальное ускорение слежения. Ранее было показано, что амплитуда ошибки при воспроизведении гармонического сигнала Δm=gm/ W(jωk), т.е. определяется модулем передаточной функции разомкнутой САУ и амплитудой входного воздействия gm. Для того, чтобы ошибка САУ не превышала Δз, желаемая л.а.х. должна проходить не ниже контрольной точки Ак с координатами: ω=ωк, L(ωк)= 20lg|W(jωk)| =20lg gm/Δm.
Известны соотношения:
g(t) = gmsin(ωkt); g'(t) = gm(ωkt); g''(t) = -gmωk2sin(ωkt);
vm = gmk; εm = gmωk2; gm = vm2/εm; ωk = εm/ vm. (6.2)
Запретная область, соответствующая системе с астатизмом 1-го порядка и обеспечивающая работу с требуемой погрешностью по амплитуде слежения, скорости и ускорению слежения, представлена на рис. 6.2.

Рис.6.2. Запретная область желаемой л.а.х.
Добротность по скорости Kν=vm/ Δm, добротность по ускорению Kε=εm/Δm. В том случае, если требуется обеспечить только статическую ошибку регулирования при подаче на вход сигнала g(t)=g0=const, то низко-частотный участок желаемой л.а.х. должен иметь наклон 0 дБ/дек и проходить на уровне 20lgKтр, где Ктр (требуемый коэффициент усиления разомкнутой САУ) рассчитывается по формуле
Δз( )=εст=g0/(1+ Ктр), откуда Ктр≥ )=εст=g0/(1+ Ктр), откуда Ктр≥  -1. -1.
Если требуется обеспечить слежение с заданной точность от задающего воздействия g(t)=νt при ν=const, то установившаяся скоростная ошибка εск( ) =ν/Ктр. Отсюда находится Ктр=ν/εcк и проводится низкочастотная часть желаемой ЛАХ с наклоном -20 дБ/дек через добротность по скорости Кν= Ктр=ν/εcк или точку с координатами: ω=1 c-1, L(1)=20lgkтр дБ. ) =ν/Ктр. Отсюда находится Ктр=ν/εcк и проводится низкочастотная часть желаемой ЛАХ с наклоном -20 дБ/дек через добротность по скорости Кν= Ктр=ν/εcк или точку с координатами: ω=1 c-1, L(1)=20lgkтр дБ.
Как было показано ранее, среднечастотный участок желаемой л.а.х. обеспечивает основные показатели качества переходного процесса - перерегулирование σ и время регулирования tп. Среднечастотный участок желаемой л.а.х. должен иметь наклон -20 дБ/дек и пересекать ось частот на частоте среза ωср, которая определяется по номограммам В.В.Солодовникова (рис.6.3). Рекомендуется учитывать порядок астатизма проектируемой системы и выбирать ωср по соответствующей номограмме.

Рис.6.3. Номограммы качества Солодовникова:
а - для астатических САУ 1-го порядка; б - для статических САУ
Так например, для σm=35% и tп=0.6 с, пользуясь номограммой (рис.6.3,а) для астатической системы 1-го порядка, получим tп=4.33 π/ωср или ωср =21.7 с-1.
Через ωср =21.7 с-1 необходимо провести прямую с наклоном -20 дБ/дек, а ширина среднечастотного участка определяется из условия обеспечения требуемого запаса устойчивости по модулю и фазе. Известны разные подходы к установлению запасов устойчивости [2,4,5]. Необходимо помнить, что чем выше в системе частота среза, тем больше вероятность того, что при расчетах скажется погрешность не учитываемых малых постоянных времени отдельных устройств САУ. Поэтому рекомендуется с ростом ωср искусственно увеличивать запасы устойчивости по фазе и модулю. Так для двух типов САУ рекомендуется пользоваться приведенной в [2] таблицей. При высоких требования к качеству переходных процессов, например,
20%<σm<24%; 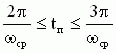 , ,
рекомендуются следующие средние показатели устойчивости: φзап=45°, Hм=16 дБ, -Hм=14 дБ.
При пониженных требованиях к качеству переходных процессов, например,
25%<σm<45%;  , ,
рекомендуются следующие средние показатели устойчивости: φзап=30°, Hм=12 дБ, -Hм=10 дБ.
На рис.6.4 приведен вид среднечастотного участка желаемой л.а.х., ширина которого обеспечивает требуемые запасы устойчивости.

Рис.6.4. Среднечастотная часть желаемой л.а.х.
После этого участки средних и низких частот сопрягаются отрезками прямых с наклонами -40 или -60 дБ/дек из условия получения наиболее простого корректирующего устройства.
Наклон высокочастотного участка желаемой л.а.х. рекомендуется оставить равным наклону высокочастотного участка располагаемой л.а.х. В этом случае корректирующее устройство будет более помехозащищенным. Согласование средне- и высокочастотного участков желаемой л.а.х. также проводится с учетом получения простого корректирующего устройства и, кроме того, обеспечения нужных запасов устойчивости.
Передаточная функция желаемой разомкнутой системы Wж(p) находится по виду желаемой л.а.х. Lж(ω). Затем строятся фазовая частотная характеристика желаемой разомкнутой САУ и переходная характеристика желаемой замкнутой системы и оцениваются реально полученные показатели качества проектируемой системы. Если они удовлетворяют требуемым значениям, то построение желаемой л.а.х. считается законченным, в противном случае построенные желаемые ЛЧХ необходимо скорректировать. Для снижения перерегулирования расширяют среднечастотный участок желаемой л.а.х. (увеличивают значение ±Hм). Для повышения быстродействия системы необходимо увеличить частоту среза.
Для определения параметров последовательного корректирующего устройства необходимо:
а) вычесть из желаемой л.а.х. Lж располагаемую л.а.х. L0, т.е. найти л.а.х. минимально-фазового корректирующего устройства Lку;
б) по виду л.а.х. последовательного корректирующего устройства Lку написать его передаточную функцию и пользуясь справочной литературой подобрать конкретную схему и реализацию.
На рис.6.5 приведен пример определения передаточной функции последовательного корректирующего устройства.

Рис.6.5. ЛАХ располагаемой L0, желаемой Lж разомкнутой системы
и последовательного корректирующего устройства Lку
После графического вычитания получаем следующую передаточную функцию корректирующего устройства

Параллельное корректирующее устройство или корректирующее устройство в виде местной обратной связи может быть получено пересчетом по формуле (6.1).
По полученной передаточной функции Wку(р) необходимо спроектировать реальное корректирующее устройство, которое может быть реализовано аппаратно или программно. В случае аппаратной реализации требуется подобрать схему и параметры корректирующего звена. В литературе [2,4,5] имеются таблицы типовых корректирующих устройств как пассивных, так и активных, как на постоянном, так и переменном токе. В том случае, если используется для управления САУ ЭВМ, то предпочтительнее программная реализация.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обуч
| Метод подчиненного регулирования
|  
|  
|  
| Большое распространение получили в настоящее время системы, построенные по принципу подчиненного регулирования, который поясняется рис.6.6. В системе предусматривается n контуров регулирования со своими регуляторами Wpi(p), причем выходной сигнал регулятора внешнего контура является предписанным значением для внутреннего контура, т.е. работа каждого внутреннего контура подчинена внешнему контуру.

Рис.6.6. Структурная схема САУ подчиненного регулирования
Два главных достоинства определяют работу систем подчиненного регулирования.
1. Простота расчета и настройки. Настройка в процессе наладки ведется начиная с внутреннего контура. Каждый контур включает в себя регулятор, за счет параметров и структуры которого получаются стандартные характеристики. Причем в каждом контуре компенсируется наибольшая постоянная времени.
2. Удобство ограничения предельных значений промежуточных координат системы. Это достигается за счет ограничения определенным значением выходного сигнала регулятора внешнего контура.
Вместе с тем, из принципа построения системы подчиненного регулирования очевидно, что быстродействие каждого внешнего контура будет ниже быстродействия соответствующего внутреннего контура. Действительно, если в первом контуре частота среза л.а.х. составит 1/2Tμ, где 2Tμ- сумма малых нескомпенсированных постоянных времени, то даже при отсутствии во внешнем контуре других звеньев с малыми постоянными времени, частота среза его л.а.х. будет 1/4Tμ и т.д. Поэтому системы подчиненного регулирования редко строятся с числом контуров больше трех.
Возьмем типовой контур рис.6.7 и настроим его на модульный (МО) и симметричный (СО) оптимумы.

Рис.6.7. Схема типового контура
На схеме рис.6.7 обозначены: Тμ - сумма малых постоянных времени;
То - большая постоянная времени, подлежащая компенсации; Кε и КO - соответственно коэффициенты усиления блоков с малыми постоянными времени и объекта управления. Следует заметить, что от типа звена, постоянную времени которого следует компенсировать, зависит и тип регулятора Wp(p). Он может быть П, И, ПИ и ПИД. В качестве примера возьмем ПИ - регулятор:
 . .
Для модульного оптимума выберем параметры:

Тогда передаточная функция разомкнутого контура будет иметь вид:

Логарифмические частотные характеристики, соответствующие передаточной функции W(p), изображены на рис.6.8,а.

Рис.6.8. ЛЧХ и h(t) при модульной настройке
При ступенчатом управляющем воздействии выходная величина в первый раз достигает установившегося значения через время 4,7Тμ, перерегулирование составляет 4,3%, а запас по фазе 63° (рис.6.8, б). Передаточная функция замкнутой САУ имеет вид

Если представить характеристическое уравнение замкнутой САУ в виде Т2р2+2ξТр+1=0, то коэффициент демпфирования при модульном оптимуме имеет величину  . В тоже время видно, что время регулирования не зависит от большой постоянной времени То. Система имеет астатизм первого порядка. При настройке системы на симметричный оптимум выбирают параметры ПИ - регулятора следующим образом: . В тоже время видно, что время регулирования не зависит от большой постоянной времени То. Система имеет астатизм первого порядка. При настройке системы на симметричный оптимум выбирают параметры ПИ - регулятора следующим образом:

Тогда передаточная функция разомкнутого контура имеет вид
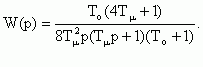
Настройка на СО рекомендуется тогда, когда в САУ То>>4Тμ. В этом случае можно принять 1/(То+1)=1/То. Тогда передаточная функция разомкнутой САУ приобретает вид

Соответствующие ей логарифмические частотные характеристики и график переходного процесса представлены на рис.6.9.

Рис.6.9. ЛЧХ и h(t) при настройке на симметричный оптимум
Время первого достижения выходной величиной установившегося значения составляет 3,1Тμ, максимальное перерегулирование достигает 43%, запас по фазе -37°. САУ приобретает астатизм второго порядка. Следует отметить, что если звено с наибольшей постоянной времени представляет собой апериодическое 1-го порядка, то с ПИ - регулятором при То=4Тμ переходные процессы соответствуют процессам при настройке на МО. Если То<4Тμ, то настройка регулятора на τ=Тμтеряет смысл. Необходимо выбрать другой тип регулятора.
В ТАУ известны и другие типы оптимальных настроек регуляторов, например:
- биномиальная, когда характеристическое уравнение САУ представляется в виде (p+ω0)n - где ω0- модуль n - кратного корня;
- баттерворта, когда характеристические уравнения САУ различных порядков имеют вид

Эти настройки целесообразно применять, когда в системе используется модальное управление по каждой координате.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
| Построение переходного процесса
|  
|  
|  
| Существуют три группы методов построения переходных процессов: аналитические; графические, использующие частотные и переходные характеристики; построение переходных процессов с помощью ЭВМ. В наиболее сложных случаях используются ЭВМ, которые позволяют кроме моделирования САУ, подключать к машине отдельные части реальной системы, т.е. близки к экспериментальному методу. Первые две группы используются в основном в случае простых систем, а также на этапе предварительного исследования при существенном упрощении системы.
Аналитические методы основаны на решении дифференциальных уравнений системы или определении обратного преобразования Лапласа от передаточной функции системы.
Расчет переходных процессов по частотным характеристикам используют тогда, когда анализ САУ с самого начала ведется частотными методами. В инженерной практике для оценки показателей качества и построения переходных процессов в системах автоматического управления получил распространение метод трапецеидальных частотных характеристик, разработанный В.В.Солодовниковым [2,4,13].
Установлено, что если на систему действует единичное задающее воздействие, т.е. g(t)=1(t), а начальные условия являются нулевыми, то реакцию системы, которая представляет собой переходную характеристику, в этом случае можно определить как
 (6.3) (6.3)
 (6.4) (6.4)
где P(ω) - вещественная частотная характеристика замкнутой системы; Q(ω) - мнимая частотная характеристика замкнутой системы, т.е. Фg(jω)=P(ω)+jQ(ω).
Метод построения заключается в том, что построенную вещественную характеристику P(ω) разбивают на ряд трапеций, заменяя приближенно кривые линии прямолинейными отрезками так, чтобы при сложении всех ординат трапеций получилась исходная характеристика рис.6.10.

Рис.6.10. Вещественная характеристика замкнутой системы
где: ωрi и ωсрi - соответственно частота равномерного пропускания и частота среза каждой трапеции.
Затем для каждой трапеции определяется коэффициент наклона ωрi/ωсрi и по таблице h-функций строятся переходные процессы от каждой трапеции hi. В таблице h-функций дано безразмерное время τ. Для получения реального времени ti необходимо τ разделить на частоту среза данной трапеции. Переходный процесс для каждой трапеции необходимо увеличить в Pi(0) раз, т.к. в таблице h-функций даны переходные процессы от единичных трапеций. Переходный процесс САУ получается алгебраическим суммированием построенных hi процессов от всех трапеций.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
1. Что понимается под улучшением качества процесса управления и как это достигается?
2. Назовите линейный стандартный закон управления.
3. Расскажите о типовых законах управления и типовых регуляторах.
4. Каково назначение корректирующих устройств? Укажите способы их включения и особенности.
5. Поясните постановку задачи синтеза систем.
6. Перечислите этапы синтеза систем.
7. Объясните построение желаемой ЛАХ проектируемой системы.
8. Каким образом формируется передаточная функция разомкнутой проектируемой системы?
9. Как определяются передаточные функции корректирующих устройств?
10. Каковы достоинства и недостатки параллельных и последовательны корректирующих устройств?
11. Каким образом пользуются номограммами "замыкания"?
12. Перечислите методы построения переходных процессов.
13. Как по вещественной характеристике определить установившееся значение переходного процесса?
14.Как изменить желаемую л.а.х. для повышения запасов устойчивости?
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обу
Тема №7: Нелинейные САУ
Большинство характеристик реальных устройств в общем случае являются нелинейными и некоторые из них не могут быть линеаризованы, т.к. имеют разрывы второго рода и к ним кусочно-линейная аппроксимация неприменима. Работу реальных звеньев (устройств) могут сопровождать такие явления, как насыщение, гистерезис, люфт, наличие зоны нечувствительности и т.д. Нелинейности могут быть естественными и искусственными (преднамеренно вводимые). Естественные нелинейности присущи системам в силу нелинейного проявления физических процессов и свойств у отдельных устройств. Например, механическая характеристика асинхронного двигателя. Искусственные нелинейности вводятся разработчиками в системы, чтобы обеспечить требуемое качество работы: для оптимальных по быстродействию систем применяют релейное управление, наличие нелинейных законов в поисковых и безпоисковых экстремальных системах, системы с переменной структурой и т.д.
Нелинейной системой называется такая система, в состав которой входит хотя бы один элемент, линеаризация которого невозможна без потери существенных свойств системы управления в целом. Существенными признаками нелинейности являются: если некоторые координаты или их производные по времени входят в уравнение в виде произведений или степени, отличной от первой; если коэффициенты уравнения являются функциями некоторых координат или их производных. При составлении дифференциальных уравнений нелинейных систем сначала составляют дифференциальные уравнения для каждого устройства системы. При этом характеристики устройств, допускающих линеаризацию, линеаризуются. Элементы, не допускающие линеаризации, называются существенно нелинейными. В результате получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть. В простейшем случае структурная схема САУ нелинейной системы представляет собой последовательное соединение безынерционного нелинейного элемента и линейной части, охваченное обратной связью (рис.7.1). Так как для нелинейных систем не применим принцип суперпозиции, то, проводя структурные преобразования нелинейных систем, единственным ограничением по сравнению со структурными преобразованиями линейных систем, является то, что нельзя переносить нелинейные элементы через линейные и наоборот.
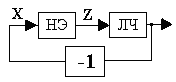
Рис. 7.1. Функциональная схема нелинейной системы:
НЭ - нелинейный элемент; ЛЧ - линейная часть; Z(t) и X(t)
соответственно выход и вход нелинейного элемента.
Классификация нелинейных звеньев возможна по различным признакам. Наибольшее распространение получила классификация по статическим и динамическим характеристикам. Первые представляются в виде нелинейных статических характеристик, а вторые - в виде нелинейных дифференциальных уравнений. Примеры таких характеристик приведены в [2,6]. На рис.7.2. приведены примеры однозначных (без памяти) и многозначных (с памятью) нелинейных характеристик. В этом случае учитывается направление (знак) скорости сигнала на входе.

Рис.7.2. Статические характеристики нелинейных элементов
Поведение нелинейных систем при наличии существенных нелинейностей имеет ряд особенностей, отличных от поведения линейных САУ [2,6,13 ]:
1. выходная величина нелинейной системы непропорциональна входному воздействию, т.е. параметры нелинейных звеньев зависят от величины входного воздействия;
2. переходные процессы в нелинейных системах зависят от начальных условий (отклонений). В связи с этим, для нелинейных систем введены понятия устойчивости "в малом", "в большом", "в целом". Система устойчива "в малом", если она устойчива при малых (бесконечно малых) начальных отклонениях. Система устойчива "в большом", если она устойчива при больших (конечных по величине) начальных отклонениях. Система устойчива "в целом", если она устойчива при любых больших (неограниченных по величине) начальных отклонениях. На рис.7.3 приведены фазовые траектории систем: устойчивой "в целом" (а) и системы устойчивой "в большом" и неустойчивой "в малом" (б);
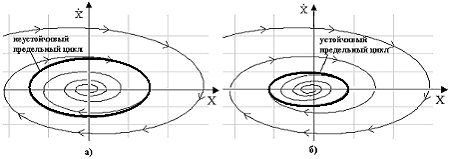
Рис.7.3. Фазовые траектории нелинейных систем
3. для нелинейных систем характерен режим незатухающих периодических колебаний с постоянной амплитудой и частотой (автоколебаний), возникающий в системах при отсутствии периодических внешних воздействий;
4. при затухающих колебаниях переходного процесса в нелинейных системах возможно изменение периода колебаний.
Эти особенности обусловили отсутствие общих подходов при анализе и синтезе нелинейных систем. Разработанные методы позволяют решать лишь локальные нелинейные задачи. Все инженерные методы исследования нелинейных систем разделяются на две основные группы: точные и приближенные. К точным методам относится метод А.М.Ляпунова, метод фазовой плоскости, метод точечных преобразований, частотный метод В.М.Попова. Приближенные методы основаны на линеаризации нелинейных уравнений системы с применением гармонической или статистической линеаризации. Границы применимости того или иного метода буду рассмотрены ниже. Следует заметить, что в обозримом будущем имеется необходимость дальнейшего развития теории и практики нелинейных систем.
Мощным и эффективным методом исследования нелинейных систем является моделирование, инструментарием которого служит компьютер. В настоящее время многие сложные для аналитического решения теоретические и практические вопросы сравнительно легко могут быть решены с помощью вычислительной техники.
Основными параметрами, характеризующими работу нелинейных САУ, являются:
1. Наличие или отсутствие автоколебаний. Если автоколебания имеются, то необходимо определить их амплитуду и частоту.
2. Время выхода регулируемого параметра в режим стабилизации (быстродействие).
3. Наличие или отсутствие скользящего режима.
4. Определение особых точек и особых траекторий движения.
Это далеко не полный перечень исследуемых показателей, сопровождающих работу нелинейных систем. Системы экстремальные, самонастраивающиеся, с переменными параметрами требуют оценки и дополнительных свойств.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
| Метод гармонического баланса
|  
|  
|  
| Идея метода гармонической линеаризации принадлежит Н.М. Крылову и Н.Н. Боголюбову и базируется на замене нелинейного элемента системы линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Метод является приближенным и может быть использован только в случае, когда линейная часть системы является фильтром низких частот, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники. При этом линейная часть может быть описана дифференциальным уравнением любого порядка, а нелинейный элемент может быть как однозначным, так и многозначным.
В основе метода гармонической линеаризации (гармонического баланса) лежит предположение, что на вход нелинейного элемента подается гармоническое воздействие с частотой ω и амплитудой А, т.е. x = А sinωt. В предположении, что линейная часть является фильтром низких частот, спектр выходного сигнала линейной части ограничивается только первой гармоникой, определяемой рядом Фурье (в этом и заключается приближенность метода, т.к. высшие гармоники выбрасываются из рассмотрения). Тогда связь между первой гармоникой выходного сигнала и входным гармоническим воздействием нелинейного элемента представляется в виде передаточной функции [2,4,13]:
 (7.1) (7.1)
Уравнение (7.1) называется уравнением гармонической линеаризации, а коэффициенты q и q' - коэффициентами гармонической линеаризации, зависящие от амплитуды А и частоты ω входного воздействия. Для различных видов нелинейных характеристик коэффициенты гармонической линеаризации сведены в таблицу [2,4,13]. Следует заметить. что для статических однозначных коэффициент q'(А)=0. Подвергнув уравнение (7.1) преобразованию по Лапласу при нулевых начальных условиях с последующей заменой оператора p на jω (p = jω), получим эквивалентный комплексный коэффициент передачи нелинейного элемента
Wнэ(jω,A) = q + jq'. (7.2)
После того, как проведена гармоническая линеаризация, для анализа и синтеза нелинейных САУ возможно применение всех методов, применяемых для исследования линейных систем, в том числе и использование различных критериев устойчивости. При исследовании нелинейных систем на основе метода гармонической линеаризации в первую очередь решают вопрос о существовании и устойчивости периодических (автоколебательных) режимов. Если периодический режим устойчив, то в системе существуют автоколебания с частотой ω0 и амплитудой А0. Рассмотрим нелинейную систему, включающую в себя линейную часть с передаточной функцией
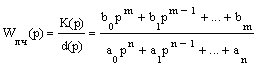 (7.3) (7.3)
и нелинейный элемент с эквивалентным комплексным коэффициентом передачи (7.2). Расчетная структурная схема нелинейной системы приобретает вид рис.7.5.

Рис.7.5. Структурная схема нелинейной САУ
Для оценки возможности возникновения автоколебаний в нелинейной системе методом гармонической линеаризации необходимо найти условия границы устойчивости, как это делалось при анализе устойчивости линейных систем. Если линейная часть описывается передаточной функцией (7.3), а нелинейный элемент (7.2), то характеристическое уравнение замкнутой системы будет иметь вид
d(p) + k(p)(q(ω,A) + q'(ω,A)) = 0 (7.4)
На основании критерия устойчивости Михайлова границей устойчивости будет прохождение годографа Михайлова через начало координат. Из выражений (7.4) можно найти зависимость амплитуды и частоты автоколебаний от параметров системы, например, от коэффициента передачи k линейной части системы. Для этого необходимо в уравнениях (7.4) коэффициент передачи k считать переменной величиной, т.е. это уравнение записать в виде:
d(jω) + K(jω)(q(ω,A) + q'(ω,A)) = Re(ω0,A0,K) +Jm(ω0,A0,k) = 0 (7.5)
где ωo и Ao - возможные частота и амплитуда автоколебаний.
Тогда, приравнивая к нулю действительную и мнимую части уравнения (7.5)
 (7.6) (7.6)
можно построить границу устойчивост
|










 (6.1)
(6.1) ) не должна превышать заданное значение Δ(
) не должна превышать заданное значение Δ(
 -1.
-1.
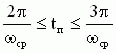 ,
, ,
,




 .
.



 . В тоже время видно, что время регулирования не зависит от большой постоянной времени То. Система имеет астатизм первого порядка. При настройке системы на симметричный оптимум выбирают параметры ПИ - регулятора следующим образом:
. В тоже время видно, что время регулирования не зависит от большой постоянной времени То. Система имеет астатизм первого порядка. При настройке системы на симметричный оптимум выбирают параметры ПИ - регулятора следующим образом:
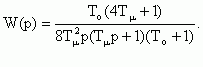



 (6.3)
(6.3)  (6.4)
(6.4)



 (7.1)
(7.1)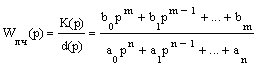 (7.3)
(7.3)
 (7.6)
(7.6)


