Тема №8: импульсные и цифровые сау
Похожие статьи вашей тематики
Дискретной линейной системой автоматического регулирования называется система, в которую помимо звеньев, описываемых обыкновенными линейными дифференциальными уравнениями, входят одно или несколько звеньев, производящих квантование непрерывного сигнала в дискретный с помощью или импульсного элемента, или цифрового устройства. В импульсных системах производится квантование сигнала по времени, в цифровых - по времени и по уровню.
Линейной системой импульсного регулирования называется такая САУ, которая кроме непрерывной части, содержащей типовые динамические звенья, состоит из импульсных элементов (одного или нескольких), преобразующих непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы. Варианты выходных последовательностей импульсных звеньев приведены на рис. 8.1.

Рис.8.1. Линейные импульсные последовательности
Основным достоинством применения импульсных систем является то, что квантование (прерывание) сигнала по времени, позволяет получать весьма большие коэффициенты усиления по мощности. Кроме того, при импульсном режиме уменьшается расход потребляемой энергии системы, увеличивается помехозащищенность.
Цифровые системы строятся на базе комплекса средств вычислительной техники, основными элементами которого являются: ЦВМ, устройства ввода, устройства вывода. Устройствами ввода и вывода в случае состыковки с аналоговыми сигналами являются АЦП и ЦАП-ы, а в случае состыковки с цифровыми сигналами - порты и интерфейсы. В системах с ЦВМ, последние могут выполнять роли: регулятора, регулятора и устройства сравнения, корректирующего устройства или самого объекта. Во всех случаях ЦВМ предоставляет легко доступные информационные потоки, позволяющие кроме прямого управления осуществлять функции: контроля, оптимизации, координации и организации всех процессов.
В общем случае импульсная (цифровая) система состоит из импульcного элемента (ИЭ) и преобразованной непрерывной части (НЧ), приведенная функциональная схема которой представлена на рис.8.2.

Рис. 8.2. Функциональная схема импульсной системы
Процесс импульсной модуляции состоит в изменении по определенному временному закону какого-либо параметра периодически повторяющихся импульсов, как показано на рис.8.1. для линейных импульсных систем, где в зависимости от того, какой из параметров последовательности импульсов изменяется по закону изменения модулирующей величины представлена классификация только линейных импульсных систем:
- амплитудно-импульсную модуляцию - АИМ (амплитуда импульса пропорциональна входному сигналу: A = f(x);
- широтно-импульсную модуляцию - ШИМ (длительность импульса пропорциональна входному сигналу: Тимп = f(x) при A = const;)
Кроме того, различают два рода импульсной модуляции. Если параметры последовательности импульсов изменяются в зависимости от значений модулирующей величины в фиксированные равноотстоящие друг от друга моменты времени, то такой вид модуляции называется импульсной модуляцией первого рода - АИМ 1-рода. Если же параметры последовательности импульсов изменяются в соответствии с текущим значением модулирующей величины, то такой вид модуляции называется импульсной модуляцией второго рода - АИМ 2-го рода (но эта классификация не ухудшает погрешностей расчетов). В нелинейных импульсных системах параметры импульсного элемента или непрерывной части системы зависят не только от внешнего воздействия, но и величин, характеризующих состояние системы (импульсные системы с переменными параметрами).
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
| Описание импульсных систем
|  
|  
|  
| Расчет импульсных и цифровых систем ведется с применением решетчатых функций и разностных уравнений. Решетчатые функции рис.8.3,б определяются только в дискретные моменты времени [nT] (сокращенно [n]), и формируются из непрерывных функций рис.8.3,а f [nT] = f (t) при t=nT. Рассматриваются так же смещенные решетчатые функции (последовател-ность рис.8.3,в) f [n,ε] = f (t) при t=(n+ε)T, где ε - относительное смещение, 0 < ε < 1.

Рис.8.3. Типы решетчатых функций
При определении решетчатых функций необходимо пользоваться теоремой Котельникова-Шеннона [2,4]: непрерывный сигнал f(t), частотный спектр которого ограничен полосой 0 < f < fп, полностью определяется последовательностью своих дискретных значений, если период повторения Т этих значений удовлетворяет условию
Т <  или Т < или Т <  , где fп[Гц], ωп [с-1] - частота пропускания. (8.1) , где fп[Гц], ωп [с-1] - частота пропускания. (8.1)
Непрерывные функции, проходящие через дискреты рассматриваемой решетчатой функции, называют огибающими. Их может быть проведено бесчисленное множество. В дальнейших расчетах используется только одна - основная. Основная огибающая это такая кривая, которая может быть описана уравнением наименьшего порядка и должна содержать гармоники наименьшей частоты (рис.8.4).

Рис.8.4. Синтез основной огибающей функции
Аналогом первой производной для решетчатой функции является:
первая прямая разность Δ f [n] =f [n+1] - f [n];
первая обратная разность: 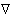 f [n] = f [n] - f [n-1]. f [n] = f [n] - f [n-1].
Аналогов второй производной являются вторые разности:
прямая Δ2 f [n] = Δ f [n+1] - Δ f [n] = (f [n+2] - f [n+1]) - (f [n+1] - f [n]) = f [n+2] - 2 f [n+1] + f [n];
обратная 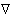 2 f [n] = 2 f [n] = 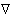 f [n] - f [n] - 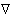 f [n-1] = f [n] - 2 f [n-1] + f [n-2]. f [n-1] = f [n] - 2 f [n-1] + f [n-2].
По аналогии можно определить разности высшего порядка с использованием рекуррентных соотношений:
 ; ; 
где  . .
Аналогами интеграла непрерывной функции в пределах от 0 до t для решетчатой функции являются:
неполная сумма 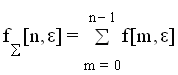 ; ;
полная сумма 
Отличие этих сумм заключается в том, что значение f[n,ε] в момент времени t = nT + εT также участвует в формировании результата.
Аналогом дифференциальных уравнений для импульсной системы является уравнение в конечных разностях или разностное уравнение (РУ):
b0Δmy[n] + b1Δm-1y[n] +... + bmy[n] = f [n].
Если раскрыть разности, то уравнение будет иметь вид:
a0y[n] + a1y[n-1] +... + amy[n-m] = f [n], (8.2)
 
Представим y[n], y[n-1],..., y[n-m], применяя операцию сдвига (свертки) и учитывая запаздывание оператором е-рТ, в операторной форме и, вынося изображение дискретной последовательности y[n] в уравнении (8.2) за скобку, получим
(а0 + а1е-Тр +...+ аmе-mTp) Y#(p)=F#(p). (8.3)
Введем обозначение z = eTр и перепишем уравнение (8.3)
(a0 + a1 z-1 +... + amz -m) Y[z] = F[z].
Для решетчатых функций времени введено понятие дискретного преобразования Лапласа
  (8.4) (8.4)
которое называется z-преобразованием при подстановке z = eTр, и связывает изображение с оригиналом. Для нахождения z-изображений решетчатых функций по заданному оригиналу, и наоборот, имеются специальные таблицы [2,9]. Определены правила и теоремы для математических действий с ними. Необходимо отметить, что все функции времени, имеющие одинаковые значения в дискретные моменты времени, обладают одинаковыми z-преобразованиями и поэтому связь между функцией времени и ее z-изображением не является взаимно однозначной.
Для обобщенной импульсной системы, представленной на рис.8.2, приведем некоторые понятия и соотношения:
1. если время замкнутого состояния ключа мало, то сигнал на его выходе можно заменить последовательностью f*[nT] дельта-функций, с площадью f[nT]: f*[nT] = f[nT] σ(t-nT);
2. реакция непрерывной части Wнч(р) - это суперпозиция весовых функций w(t), которую можно рассматривать и как непрерывный сигнал y(t), и как дискретную последовательность y[nT];
3. импульсным фильтром считают импульсный элемент (ключ) с непрерывной частью Wнч(р) на выходе. За истинный сигнал фильтра принимают выходную последовательность только в дискретные моменты времени y[nT], где n =..., -2, -1, 0, 1, 2,...
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочно
| Передаточные функции импульсных фильтров
|  
|  
|  
| На рис.8.5 представлена модель импульсного элемента ИЭ из рис.8.2.

Рис.8.5. Модель импульсного элемента
Задача идеального импульсного элемента (ИИЭ) в модели - сформировать для дальнейшего математического описания системы либо последовательность импульсов типа σ-функций с площадью f(t), либо решетчатую функцию, в основе которой единичная импульсная функция σo(t) = { 1 при t равном 0; 0 при t не равном 0 } с амплитудой f(t).
Задача экстраполятора (Э) - математически описать выходную последовательность реального импульсного звена (экстраполяция - это прогнозирование (синтез) сигнала между значениями решетчатой функции).
Коэффициент передачи квантователя (ИИЭ) обратно пропорционален периоду квантования, а коэффициент передачи экстраполятора нулевого порядка равен периоду. Таким образом, общий коэффициент передачи квантующей и восстанавливающей цепи, т.е. ИЭ обычно равен единице.
Если ИИЭ выдает решетчатую функцию, то можно ввести понятие "приведенной весовой функции" - wп. Это реакция на единичный импульс, поданной на вход экстраполятора. Если ИИЭ выдает последовательность типа σ-функций, то для непрерывной части совместно с экстраполятором можно вывести понятие приведенной непрерывной передаточной функции:
Wп(р) = Wэ(р)Wнч(р), при этом Wп(р) = L{ wп(t) }.
Тогда для исследования импульсной системы ее структура приводится к расчетной схеме, как показано на рис.8.6.
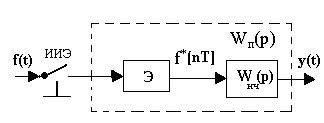
Рис.8.6. Расчетная функциональная схема разомкнутой импульсной системы
Идеальный импульсный элемент преобразует непрерывный сигнал в мгновенные импульсы в виде σ-функций, модулированные по площади, а экстраполятор формирует импульсы заданной формы из σ-функций, соответствующие форме выходного импульса реального импульсного элемента. Реальные импульсы, проходя через линейную часть, вновь образуют непрерывный сигнал y(p).
Пользуясь дискретным преобразованием Лапласа (8.4) можно найти дискретную приведенную передаточную функцию экстраполятора и непрерывной части
 (8.5) (8.5)
Структурные преобразования импульсные систем несколько отличаются от структурных преобразований линейных непрерывных САУ. В случае, когда приведенная непрерывная часть состоит из параллельно включенных звеньев и на входе имеется общее импульсное звено, то дискретная передаточная функция может быть определена суммированием дискретных передаточных функции, определенных для каждого звена в отдельности.
 . (8.6) . (8.6)
Если непрерывные звенья включены последовательно и имеется одно импульсное звено на входе, то дискретная передаточная функция такого соединения
 . .
В этом случае дискретная передаточная функция W(z) должна определяться z - преобразованием от произведения передаточных функций непрерывной части системы
W(z) = Z { W1(р) … Wi(p) }, те. W(z)  W1(z) … Wi(z)!!! W1(z) … Wi(z)!!!
Нельзя переносить сумматор или любое непрерывное звено через импульсный элемент. Непрерывную часть можно преобразовывать по известным правилам преобразования структурных схем непрерывных САУ. Для схем, состоящих из импульсных фильтров, когда на входе каждого непрерывного звена стоит свой импульсный элемент, справедливы все правила преобразования структурных схем непрерывных систем. Для нахождения дискретных передаточных функций можно пользоваться таблицами соответствий между функциями времени, их изображениями по Лапласу и их z-изображениями [2,6].
Найдем дискретные передаточные функции для различных экстраполяторов. Для экстраполятора нулевого порядка рис.8.1 изображение импульса

Тогда z - изображение экстраполятора и непрерывной части:
 (8.7) (8.7)
Если учесть наличие в непрерывной части звена чистого запаздывания е-рτ, то дискретная передаточная функция в общем виде будет:
 (8.8) (8.8)
где ε - относительное смещение, отсчитываемое от начала предыдущего такта ε=1 - τ/T; 0<τ<T.
Для импульсной системы с экстраполятором, осуществляющим АИМ-первого или второго рода (рис.8.1) изображение прямоугольного импульса единичной высоты и длительности γT можно представить как

Тогда z - изображение экстраполятора и непрерывной части:
 , где ε=1-γ (8.9) , где ε=1-γ (8.9)
Если импульсный элемент генерирует короткие по сравнению с периодом дискретности прямоугольные импульсы, т.е. γ << 1, то можно приближенно принять е-γТp=1 - γTp. Тогда получим
 (8.10) (8.10)
Формула (8.10) справедлива, если пренебречь влиянием конечной длительности импульса. В большинстве случаев для выполнения этого достаточно, чтобы постоянные времени непрерывной части системы были больше длительности импульса, т.е. Ti >> γТ (i = 1, 2, 3,...).
Пример задачи
Отметим некоторые особенности определения передаточных функций замкнутых импульсных систем. На рис.8.7 приведена структурная схема замкнутой системы, которая содержит один импульсный элемент ИЭ, одно управляющее воздействие g(t) и одно возмущающее f(t). При этом f(t) приложено ко входу непрерывной части W2(p).

Рис. 8.7. Структурная схема замкнутой импульсной системы
Для получения передаточных функций замкнутых систем по управляющему и возмущающему воздействиям а также по ошибкам от этих воздействий, целесообразно сначала привести возмущающее воздействие ко входу импульсной системы, чтобы в дальнейшем исключить ошибки определения z - преобразования от различных воздействий (рис.8.8).

Рис. 8.8. Приведенная структурная схема замкнутой импульсной системы
Тогда значения выходной величины Y(z) и ошибки Е(z) определятся выражениями:
 - от возмущающего воздействия; - от возмущающего воздействия;
 - от управляющего воздействия; - от управляющего воздействия;
 - от управляющего воздействия; - от управляющего воздействия;
W(z)=Z {Wэ(р)W1(p)W2(p)} - z- изображение разомкнутой системы.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
Частотные характеристики импульсных систем определяются так же, как и для непрерывных систем. Выражения для частотных характеристик импульсных систем получаются из их дискретных передаточных функций путем замены оператора z на ejωT. Так как частота входит в показатель степени числа e, то частотные характеристики являются периодическими функциями частоты, период изменения которых равен ±π/T. Следовательно, нельзя различить составляющие, частоты которых кратны частоте квантования импульсного элемента ω0 = 2π/Т0.
Свойства частотных характеристик импульсных систем [2]:
1. в соответствии с периодичностью частотной передаточной функции амплитудно-фазовая частотная характеристика W(ejωT) полностью определяется своими значениями в интервале -π/Т0≤ω≤π/ Т0;
2. так как вещественная частотная характеристика является четной функцией, а мнимая - нечетной, то достаточно рассматривать интервал частот 0≤ω≤π/Т0;
3. в крайних точках интервала 0≤ω≤π/T0 амплитудно-фазовая частотная характеристика принимает вещественные значения;
4. при уменьшении периода дискретности T0, т.е. при увеличении частоты квантования ω0=2π/Т0, частотные характеристики импульсных систем приближаются к частотным характеристикам непрерывных систем. При этом частотный интервал 0≤ω≤π/Т0 растягивается на всю ось ω при T0->0.
Здесь, как и в случае анализа непрерывных систем, следует заметить, что наибольшее применение в инженерной практике нашли ЛЧХ. Применение а.ф.х. и др. связано с громоздкостью вычислений, так как они описываются трансцендентными выражениями W(ejωT). Для преодоления этого затруднения на практике применяются частотные характеристики относительно абсолютной псевдочастоты λ. Переход к псевдочастоте основан на переходе от z-преобразования к w-преобразованию с помощью подстановки
 => =>  где w = jλT/2. (8.11) где w = jλT/2. (8.11)
Физически подстановка означает переход к дифференциальным уравнениям заменой в разностных уравнениях элементов чистого запаздывания грубой аппроксимацией - одним фазосдвигающим звеном. При этом реальная частота и псевдочастота λ связаны соотношением
 (8.12) (8.12)
В этом случае как и для линейных непрерывных систем частотные характеристики строятся для диапазона -  <λ<+ <λ<+  . В тоже время при выполнении условия ωT0<2, частотные характеристики непрерывных и импульсных систем совпадают. Это практически выполняется, так как частоту дискретизации 1/Т0 выбирают в 6…10 раз больше частоты среза. Тогда λ приблизительно равна ω. Поэтому для переходов часто используют формулы "Билинейного преобразования": . В тоже время при выполнении условия ωT0<2, частотные характеристики непрерывных и импульсных систем совпадают. Это практически выполняется, так как частоту дискретизации 1/Т0 выбирают в 6…10 раз больше частоты среза. Тогда λ приблизительно равна ω. Поэтому для переходов часто используют формулы "Билинейного преобразования":

Такой переход позволяет:
1. после w-преобразования, используя W(w) можно применять обычные (в основном алгебраические) критерии устойчивости, справедливые для непрерывных систем;
2. после последующего перехода в область псевдочастот (подстановка w = jλT0/2) вид передаточных функций W(jλT0/2) становится пригоден для применения методов, использующих ЛЧХ;
3. оценку качества в установившихся режимах удобно выполнять также используя предельные свойства предельного преобразования Лапласа.
В свете сказанного, однако, следует признать, что недостатком линейных систем является тот факт, что любой переходный процесс будет иметь бесконечную длительность. Это объясняется тем, что при уменьшении значений сигналов на входах интеграторов пропорционально уменьшается скорость изменения их выходных координат. В импульсных системах на время периода квантования сигнал в цепи обратной связи остается (запаздывание) на время периода квантования достаточным, чтобы добиться конечной длительности переходного процесса. Это возможно при правильном выборе периода квантования.
В инженерной практике синтез систем с ЦВМ ведется с применением логарифмических частотных характеристик. Для удобства логарифмические частотные характеристики строятся отдельно для областей низких и высоких частот. Границей, разделяющей частотную область на низкочастотную и высокочастотную, служит частота среза ωср в предположении, что  где Т0 - период дискретности. где Т0 - период дискретности.
Последнее условие необходимо выполнять вследствие требований, предъявляемых к обеспечению запаса устойчивости и точности работы системы в соответствии теоремой Котельникова-Шеннона.
В качестве примера рассмотрим методику построения ЛЧХ системы, включающей в себя экстраполятор нулевого порядка и непрерывную часть с передаточной функцией, а также выполняется условие ωср<2/Т0:
 (8.13) (8.13)
Техническая реализуемость систем с ЦВМ требует введения следующих предположений:
1. поскольку система должна быть устойчива, переход оси нуля децибел асимптотической л.а.х. непрерывной части происходит при отрицательном наклоне -20 дБ/дек;
2. постоянным времени τj (j = 1, 2,..., m) соответствуют сопрягающие частоты меньшие, чем частота среза;
3. имеется q(q < n) постоянных времени Tq (i = 1, 2,..., q), которым соответствуют сопрягающие частоты меньшие, чем частота среза.
При принятых допущениях для области низких частот передаточную функцию непрерывной части можно представить в виде
 (8.14) (8.14)
а для области высоких частот
 (8.15) (8.15)
По выражениям (8.14) и (8.15) с учетом подстановки p=jλ и умножением на множитель (1-jλT0/2) приблизительно равный 1, получим частотные характеристики разомкнутой импульсной системы для области низких частот
 (8.16) (8.16)
и для области высоких частот
 (8.17) (8.17)
где  = =  . .
Для области низких частот псевдочастота практически совпадает с угловой частотой. Влиянием дополнительного множителя при построении частотных характеристик в низкочастотной области можно пренебречь, так как ωс < 2/To. Т.е. в области низких частот частотные характеристики импульсной системы совпадают с частотными характеристиками ее непрерывной части.
Начало логарифмических частотных характеристик в высокочастотной области (8.17) сливается с концом частотных характеристик, построенных в низкочастотной области. На основании (8.16) и (8.17), а также допущений, можно записать выражение результирующей частотной передаточной функции системы
 (8.18) (8.18)
Это выражение представляет собой произведение элементарных типовых сомножителей, поэтому его легко использовать для построения логарифмических частотных характеристик импульсных систем. Результирующий фазовый сдвиг определяется как
 (8.19) (8.19)
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного
| Устойчивость импульсных систем
|  
|  
|  
| Для нахождения условий устойчивости работы импульсной системы требуется построить область устойчивости в плоскости комплексной величины z. Воспользуемся методикой D-разбиения и, меняя частоту ω от -  до + до +  , получим границу z=eTр=ejωT в виде окружности единичного радиуса. Математически это означает отображение мнимой оси плоскости корней комплексно переменной р на плоскость корней z. Заштриховав в соответствии с правилом штриховки кривую D - разбиения видим, что заштрихованная область находится внутри круга. Следовательно, для устойчивости импульсной САУ необходимо и достаточно, чтобы все полюсы передаточной функции замкнутой системы (корни характеристического уравнения) zi находились внутри этой окружности, т.е. , получим границу z=eTр=ejωT в виде окружности единичного радиуса. Математически это означает отображение мнимой оси плоскости корней комплексно переменной р на плоскость корней z. Заштриховав в соответствии с правилом штриховки кривую D - разбиения видим, что заштрихованная область находится внутри круга. Следовательно, для устойчивости импульсной САУ необходимо и достаточно, чтобы все полюсы передаточной функции замкнутой системы (корни характеристического уравнения) zi находились внутри этой окружности, т.е.
| zi | < 1, i = 1, 2,... (8.20)
Если хотя бы один корень |zi| > 1, система будет неустойчивой. Если хотя бы один |zi| = 1 при всех остальных |zn-i| < 1, в системе будут наблюдаться незатухающие колебания (граница устойчивости).
Для исследования устойчивости импульсных систем возможно использование методов исследования обыкновенных линейных систем в обычной формулировке (критериев устойчивости Гурвица, Михайлова, Найквиста), если отобразить круг единичного радиуса плоскости z на мнимую ось комплексной переменной w с помощью подстановки (8.11). В этом случае граница устойчивости вновь является прямой линией, и все корни w i должны находиться в левой полуплоскости (рис.8.10).

Рис.8.10. Расположение границ плоскостей корней
Пример задачи
Следует также заметить, что с помощью использования w - преобразования легко решаются задачи построения кривых D - разбиения по одному и двум параметрам.
Переходный процесс в импульсных системах может быть определен с помощью обратного z-преобразования, ряда Лорана, решения разностного уравнения, частотных методов, основанных на использовании вещественной или мнимой частотных характеристик замкнутой системы [9,10].
Разностное уравнение может быть найдено по дискретной передаточной функции замкнутой системы. Дискретную ПФ можно представить в любой из форм:
1.  - стандартная форма; - стандартная форма;
2. 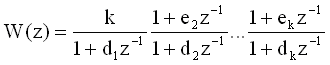 - разложение на множители; - разложение на множители;
3.  - разложение на элементарные дроби, - разложение на элементарные дроби,
где: ei и di - соответственно нули и полюса передаточной функции; a0 - не равно нулю; Pi - коэффициенты разложения
Этим формам представления дискретных передаточных функций соответствуют структурные схемы, изображенные на рис.8.11.

Рис.8.11. Расчетные структурные схемы импульсных систем
По применению различных форм представления W(z) можно привести следующие замечания:
1) разложения 2 и 3 удобны при отладке систем, позволяют контролировать промежуточные координаты xi[n] или yi[n];
2) последовательная структура 2 предпочтительна при синтезе дискретной коррекции;
3) параллельная структура 3 удобна при проектировании цифровых регуляторов и, кроме того, возможен расчет САУ с применением параллельно работающих ЦВМ, что повышает быстродействие.
Для унификации получения разностных уравнений (РУ) каждый из элементов форм 2 и 3 целесообразно представить в стандартной форме 1. Тогда разностное уравнение будет иметь вид
 (8.21) (8.21)
В разностном уравнении (8.21) значение координаты y[n] рассчитывается по предыдущим значения, поэтому оно получило название рекурсивное РУ. Решение РУ возможно как аппаратно, так и программно. Структурная схема цифрового фильтра для решения уравнения (8.21) представлена на рис.8.12.

Рис.8.12. Полная структурная схема цифрового фильтра
На рис.8.12 цепочки элементов z-1 в программах соответствуют буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации. Если выбраны формы 2 и 3, то структура каждого элемента будет иметь более простой вид рис.8.13.

Рис.8.13. Структурные схемы цифровых фильтров
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
Для импульсных систем, как и для непрерывных, введены определения статической ошибки, астатизма, коэффициентов ошибок, ошибки при гармоническом воздействии, а также средней квадратической ошибки. Точность работы импульсных систем в установившемся режиме оценивается по величине установившейся ошибки при различных типовых воздействиях. При этом целесообразно использование предельного свойства дискретного преобразования Лапласа:

где Е(z) - z - изображение ошибки регулирования.
Ниже приведены Z - преобразования для ступенчатого сигнала, линейно нарастающего и квадратичной параболы, чтобы можно было определять статические ошибки, ошибки по скорости и ускорению.
| Оригинал
| Преобразование Лапласа
| z-преобразование
| | 1(t)
| 1/p
| z/(z-1)
| | t
| 1/p2
| ZT/(z-1)2
| | t2/2
| 1/p3
| T2z(z+1)/2(z-1)3
| | e-αt
| 1/(p+α)
| z/(z-d), d=e-αT
| Для примера возьмем импульсную систему рис.8.8, z - изображения ошибок регулирования которой по управлению Eg(z) и возмущению Ef(z) имеют вид:
 ; ;  . .
В большинстве случаев ограничиваются рассмотрением ошибки в дискретные моменты времени t = nTо. Однако, надо иметь в виду, что в импульсных системах могут возникать малые колебания внутри периода дискретности в установившемся режиме. Выражение для установившейся ошибки будет
 (8.23) (8.23)
Установившиеся ошибки замкнутой импульсной системы от задающего воздействия находятся при f = 0. При g(t) = g0*1(t), имеющей G(z)= g0z/(z-1), установившаяся ошибка определяется как
 (8.24) (8.24)
и называется статической ошибкой или ошибкой системы по положению.
При g(t) = g1*t, имеющей G(z)= g1Tоz/(z-1)2, установившаяся ошибка называется скоростной ошибкой системы и определяется как
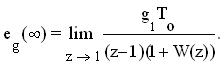 (8.25) (8.25)
Аналогично определяется ошибка по ускорению и т.д. Из последнего выражения следует, что установившаяся ошибка от задающего воздействия импульсной системы в отличие от непрерывной линейной САУ не только прямо пропорциональна величине задающего воздействия, но и периоду дискретности.
Импульсные системы классифицируются в соответствии с числом полюсов дискретной передаточной функции разомкнутой системы W(z) при z = 1. Если дискретная передаточная функция импульсной разомкнутой системы
 , ,
а W1(z) не содержит полюсов при z = 1, то при r = 0 система называется статической, при r = 1 - астатической первого порядка и т.д. В астатических системах W(1)->  . .
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
Чтобы импульсная система удовлетворяла заданным требованиям по качеству процесса управления как в установившемся режиме, так и в переходном, необходимо введение в систему корректирующих устройств и регуляторов. Для коррекции импульсных систем возможно введение непрерывных (аналоговых) корректирующих устройств, как в непрерывных системах, и, кроме того, можно вводить или видоизменять импульсные и цифровые элементы. Известно, что путем коррекции импульсных систем возможно достижение конечной длительности переходных процессов.
В случае непрерывной коррекции изменяют характеристики непрерывной части импульсной системы путем введения либо последовательных или параллельных корректирующих устройств, либо местной отрицательной или положительной обратной связи, в результате чего формируется передаточная функция желаемой системы. При расчете непрерывных корректирующих цепей целесообразно перейти от желаемой характеристики импульсной системы к желаемой характеристике ее непрерывной части. После нахождения желаемых характеристик непрерывной части задача синтеза решается так же, как она решалась для обыкновенных линейных систем автоматического управления [11].
Импульсная коррекция осуществляется включением в контур системы импульсного фильтра, который преобразует входной сигнал x в последовательность импульсов. Импульсы на выходе фильтра образуются путем амплитудно-импульсной модуляции цепи.
Цифровые корректирующие фильтры реализуются с помощью цифрового вычислителя. Устройствами ввода и вывода в случае состыковки с аналоговыми сигналами являются АЦП и ЦАП-ы, а в случае состыковки с цифровыми сигналами - порты и интерфейсы. В настоящее время широкое распространение получили цифровые системы, в которых функцию вычислительного устройства выполняют микропроцессоры и компьютеры.
Синтез цифровых систем сводится к выбору цифрового корректирующего фильтра, последовательное включение которого с непрерывной частью системы, обычно, включающей в себя объект управления, регулирующий орган, исполнительный механизм, усилитель мощности и датчик, позволяет получить систему с желаемыми характеристиками. Часто в качестве таких характеристик используют аналоговые эквиваленты [9,10]: импульсные функции, переходные функции и частотные характеристики, что обосновано при достаточно высокой тактовой частоте работы цифрового вычислителя и большой разрядности преобразователей.
Цифровая или дискретная коррекция весьма интересна с практической точки зрения в силу конструктивной универсальности устройств и гибкости настройки. Решение задачи коррекции предполагает модификацию низко
|












 или Т <
или Т <  , где fп[Гц], ωп [с-1] - частота пропускания. (8.1)
, где fп[Гц], ωп [с-1] - частота пропускания. (8.1)
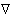 f [n] = f [n] - f [n-1].
f [n] = f [n] - f [n-1]. ;
; 
 .
.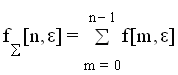 ;
;



 (8.4)
(8.4)

 (8.5)
(8.5) . (8.6)
. (8.6) .
. W1(z) … Wi(z)!!!
W1(z) … Wi(z)!!!
 (8.7)
(8.7) (8.8)
(8.8)
 , где ε=1-γ (8.9)
, где ε=1-γ (8.9) (8.10)
(8.10)

 - от возмущающего воздействия;
- от возмущающего воздействия; - от управляющего воздействия;
- от управляющего воздействия; - от управляющего воздействия;
- от управляющего воздействия; =>
=>  где w = jλT/2. (8.11)
где w = jλT/2. (8.11) (8.12)
(8.12) <λ<+
<λ<+ 
 где Т0 - период дискретности.
где Т0 - период дискретности. (8.13)
(8.13) (8.14)
(8.14) (8.15)
(8.15) (8.16)
(8.16) (8.17)
(8.17) =
=  .
. (8.18)
(8.18) (8.19)
(8.19)
 - стандартная форма;
- стандартная форма;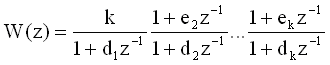 - разложение на множители;
- разложение на множители; - разложение на элементарные дроби,
- разложение на элементарные дроби,
 (8.21)
(8.21)


 ;
;  .
. (8.23)
(8.23) (8.24)
(8.24)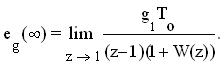 (8.25)
(8.25) ,
,


