
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифровая реализация непрерывного регулятора
Лабораторная работа № 7 Цифровая реализация непрерывного регулятора Цели работы · освоение методов переоборудования непрерывных регуляторов для реализации на цифровом компьютере Задачи работы · познакомиться с методами переоборудования непрерывных регуляторов в Matlab · научиться моделировать системы с цифровыми регуляторами · научиться выбирать интервал квантования Оформление отчета Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать · название предмета, номер и название лабораторной работы · фамилию и инициалы авторов, номер группы · фамилию и инициалы преподавателя · номер варианта · краткое описание исследуемой системы · результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы. При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова. Описание системы В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.
Структурная схема системы стабилизации судна на курсе Линейная математическая модель, описывающая рыскание судна, имеет вид
где
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией [1]
В непрерывной системе в качестве управляющего устройства используется ПИД-регулятор с передаточной функцией[2]
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с внутренней нелинейной обратной связью, охватывающей интегратор в составе регулятора[3].
Для реализации регулятора используется цифровой компьютер с интервалом квантования 1) импульсного элемента, который выбирает из непрерывного сигнала 2) линейного цифрового фильтра, который преобразует дискретную последовательность 3) восстанавливающее устройство (экстраполятор), которое восстанавливает непрерывный сигнал управления
Схема цифрового регулятора показана на рисунке:
Блок ИЭ обозначает импульсный элемент (АЦП), блок Э – экстраполятор (ЦАП). Точечные линии обозначают дискретные сигналы, сплошные линии – непрерывные. Цифровые регуляторы обладают многими преимуществами в сравнении с классическими (непрерывными): · отсутствует дрейф параметров элементов · в цифровой форме можно реализовать сложные законы управления · цифровые регуляторы легко перестраивать, настройка сводится к просто к замене алгоритма обработки измеряемых сигналов В то же время между моментами квантования (моментами съема измеряемых сигналов и выдачи нового управляющего воздействия) система ведет себя как разомкнутая (неуправляемая). Это может привести к потере устойчивости (при больших интервалах квантования в сравнении с постоянной времени объекта) и скрытым колебаниям (колебаниям непрерывного сигнала, которые не проявляются в моменты квантования). Для построения дискретной модели ПД-регулятора используется преобразование Тастина
соответствующее интегрированию по методу трапеций. Для рассматриваемого ПД-регулятора такая замена дает
где коэффициенты равны
Для построения дискретной передаточной функции интегрального канала применяется метод интегрирования Эйлера (метод прямоугольников), т.е., замена
В ходе выполнения работы требуется построить цифровые реализации регулятора при различных интервалах квантования и сравнить переходные процессы в непрерывной и цифровой системе управления. Таблица коэффициентов
Контрольные вопросы к защите 1. См. все вопросы к работам № 1–6. 2. Что такое переоборудование? 3. В чем отличие непрерывной и цифровой систем управления? 4. В чем преимущества цифровых систем управления? 5. Что такое аналоговые и дискретные сигналы? 6. Что такое дискретная передаточная функция? 7. Что такое импульсный элемент? Моделью какого реального устройства он служит? 8. Что такое экстраполятор? Моделью какого реального устройства он служит? 9. Что такое фиксатор нулевого порядка? Почему более сложные экстраполяторы применяются редко? 10. Что такое цифровой фильтр? 11. Какой оператор используется для построения дискретной передаточной функции цифрового фильтра? 12. Как найти дискретную передаточную функцию фильтра, заданного разностным уравнением? 13. Какие методы переоборудования вы знаете? Какой из них наиболее точный? 14. Как выполнить переоборудование методом Эйлера? 15. Какая функция Matlab выполняет преобразование Тастина? Как ее вызывать? 16. В чем недостаток методов переоборудования на основе формул численного интегрирования Симпсона и Уэддля? 17. Почему для переоборудования ПД-регулятора использовано преобразование Тастина, а для интегральной части – метод Эйлера? 18. Что такое алгебраический цикл? В каком случае алгебраических циклов не возникает? 19. Какие эффекты наблюдаются при увеличении интервала квантования? 20. Как обосновать выбор интервала квантования при переоборудовании непрерывного регулятора? Описание системы Исследуется нелинейная система управления судном по курсу, структурная схема которой показана на рисунке.
Движение судна описывается линейной математической моделью в виде передаточной функции
Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
В непрерывной системе в качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
где Выбор интервала квантования · переходные процессы при
· для данной системы рекомендуется выбирать интервал квантования не более … [1] Численные значения,, и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторных работах № 2–5. [2] Значение было определено в лабораторной работе № 2. [3] Значение было определено в лабораторной работе № 6. Лабораторная работа № 7 Цифровая реализация непрерывного регулятора Цели работы · освоение методов переоборудования непрерывных регуляторов для реализации на цифровом компьютере Задачи работы · познакомиться с методами переоборудования непрерывных регуляторов в Matlab · научиться моделировать системы с цифровыми регуляторами · научиться выбирать интервал квантования Оформление отчета Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать · название предмета, номер и название лабораторной работы · фамилию и инициалы авторов, номер группы · фамилию и инициалы преподавателя · номер варианта · краткое описание исследуемой системы · результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы. При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова. Описание системы В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.
Структурная схема системы стабилизации судна на курсе Линейная математическая модель, описывающая рыскание судна, имеет вид
где
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией [1]
В непрерывной системе в качестве управляющего устройства используется ПИД-регулятор с передаточной функцией[2]
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с внутренней нелинейной обратной связью, охватывающей интегратор в составе регулятора[3].
Для реализации регулятора используется цифровой компьютер с интервалом квантования 1) импульсного элемента, который выбирает из непрерывного сигнала 2) линейного цифрового фильтра, который преобразует дискретную последовательность 3) восстанавливающее устройство (экстраполятор), которое восстанавливает непрерывный сигнал управления
Схема цифрового регулятора показана на рисунке:
Блок ИЭ обозначает импульсный элемент (АЦП), блок Э – экстраполятор (ЦАП). Точечные линии обозначают дискретные сигналы, сплошные линии – непрерывные. Цифровые регуляторы обладают многими преимуществами в сравнении с классическими (непрерывными): · отсутствует дрейф параметров элементов · в цифровой форме можно реализовать сложные законы управления · цифровые регуляторы легко перестраивать, настройка сводится к просто к замене алгоритма обработки измеряемых сигналов В то же время между моментами квантования (моментами съема измеряемых сигналов и выдачи нового управляющего воздействия) система ведет себя как разомкнутая (неуправляемая). Это может привести к потере устойчивости (при больших интервалах квантования в сравнении с постоянной времени объекта) и скрытым колебаниям (колебаниям непрерывного сигнала, которые не проявляются в моменты квантования). Для построения дискретной модели ПД-регулятора используется преобразование Тастина
соответствующее интегрированию по методу трапеций. Для рассматриваемого ПД-регулятора такая замена дает
где коэффициенты равны
Для построения дискретной передаточной функции интегрального канала применяется метод интегрирования Эйлера (метод прямоугольников), т.е., замена
В ходе выполнения работы требуется построить цифровые реализации регулятора при различных интервалах квантования и сравнить переходные процессы в непрерывной и цифровой системе управления.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |


 – угол рыскания (угол отклонения от заданного курса),
– угол рыскания (угол отклонения от заданного курса),  – угловая скорость вращения вокруг вертикальной оси,
– угловая скорость вращения вокруг вертикальной оси, 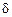 – угол поворота вертикального руля относительно положения равновесия,
– угол поворота вертикального руля относительно положения равновесия,  – постоянная времени,
– постоянная времени,  – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
– постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде .
. ,
, ,
,  .
. ,
, , где
, где  сек и
сек и  сек.
сек.
 . Регулятор в расчетной схеме заменяется не последовательное соединение трех звеньев:
. Регулятор в расчетной схеме заменяется не последовательное соединение трех звеньев: значения
значения 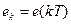 в моменты квантования
в моменты квантования  (при целых
(при целых  ); импульсный элемент моделирует аналого-цифровой преобразователь (АЦП);
); импульсный элемент моделирует аналого-цифровой преобразователь (АЦП); в управляющую последовательность
в управляющую последовательность  ; передаточная функция этого фильтра определяет закон управления;
; передаточная функция этого фильтра определяет закон управления; из последовательности
из последовательности 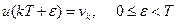 .
.
 ,
, ,
,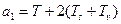 ,
,  ,
, 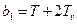 ,
,  .
. .
. , сек
, сек
 ,рад/сек
,рад/сек
 , сек
, сек
 , сек
, сек
 , где
, где 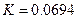 рад/сек,
рад/сек,  сек,
сек,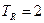 сек,
сек, сек,
сек, ,
,  сек,
сек,  сек,
сек,




