
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Амплитудно - импульсная модуляция (АИМ)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
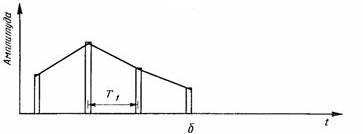
При использовании импульсных методов для передачи аналоговых сигналов необходимо сначала преобразовать аналоговые данные в импульсную форму. Это преобразование также относится к модуляции, так как аналоговые данные используются для модулирования (изменения) последовательности импульсов или импульсной поднесущей. На рис. 8, а показана модуляция синусоидальным сигналом амплитуд последовательности импульсов.
Рис. 8. Форма сигналов амплитудно-импульсной модуляции. а—форма модулированного сигнала; б—воспроизведенная форма сигнала при низкой частоте следования импульсов, Т1 — период последовательности импульсов; в — воспроизведенная форма сигнала при высокой частоте следования импульсов, Т2 — период последовательности импульсов.
Фаза импульсной последовательности Xi(t) совпадает с фазой Длительность импульса – постоянная
Здесь введено обозначение
II. Широтно – импульсная модуляция (ШИМ) Широтно-импульсная модуляция состоит в изменении ширины (длительности) импульсов, следующих друг за другом с постоянной частотой.
I. Фазово – импульсная модуляция (ФИМ)
Релейные системы. Цифровые САУ.
I. Релейные системы. Это системы с квантованием по уровню. Осуществляется релейным элементом. Так же есть квантование во времени.
Высота ступенек одинаковая (=h)
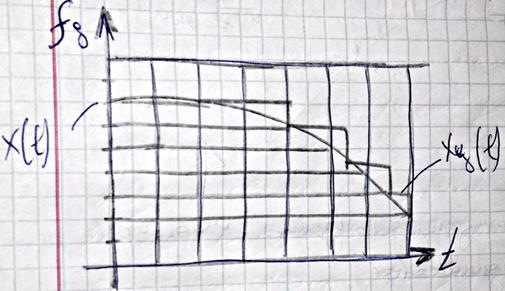
Дискретизация по уровню – многоуровневое реле. Выходной сигнал релейного элемента изменяется ступенчато в неопределенные заранее моменты времени (асинхронно) и по уровню может менять конечный, заранее определенный набор значений. В каждый момент времени это ближайшие к X(t) значения (н-р верхнее из разрешенных).
II. Цифровые системы. Имеет одновременно квантование как по уровню, так и по времени.
В электрических цепях такое преобразование осуществляет синхронный АЦП.
Формально, цифровой дискретизатор АЦП может быть представлен из 2-х частей (как последовательно соединение импульсного и решетчатого элемента)
Дискретные системы имеют в сравнении с аналоговыми ряд преимуществ: 1) Высокий собственный КПД. Особенно важно для силовых исполнительных узлов САУ. (Н-р: тиристорные и транзисторные ШИМ усилители) 2) Высокая помехозащищенность, характерная для дискретных преобразователей и их каналов передачи 3) Высокая точность обработки данных и возможность использования ЭВМ и контроллеров
Приведение дискретной САУ к эквивалентной непрерывной. Квантование во времени. Строго говоря, операции квантования не может быть противопоставлено эквивалентное непрерывное звено. Квантование во времени создает новый тип сигналов функции дискретного времени. Квантование по уровню нелинейно (принципиально не линейно 2-х уровневое реле). Вместе с тем, вполне очевидно, что если интервалы квантования по уровню или времени достаточно малы, то дискретностью сигналов можно пренебречь, рассматривая их как непрерывные функции времени, а операции в элементах дискретизации считать обычным линейным преобразованием физических величин, причем безынерционным и пропорциональным. Например, в синхронном АЦП, в преобразовании вида
при достаточно малом весе младшего разряда, при Найдем условия, при которых дискретную систему можно представить эквивалентной непрерывной. Квантование во времени
Обычно, импульсную систему представляют в виде:
Если низкочастотная часть линейна, то она описывается типовыми зависимостями. Импульсный элемент формирует импульсную последовательность Причем 1 из параметров этой последовательности пропорционально модулируемый решетчатой функцией.
Решетчатая функция представляет собой пронумерованную последовательность дискрет, которая порождает непрерывная функция X(t).
Импульсный элемент можно представить в виде 2-х составляющих:
1 – идеальный импульсный элемент. Он генерирует моделированную входным сигналом последовательность дельта – функции.
2 – ФЦ – формирующая цепь непрерывного действия (реакция S(t); которая на каждый импульс равна заданной форме импульса, последовательности Наиболее просто представить для случая импульсной модуляции. Достаточно выбрать в качестве формирующей цепи линейное звено с весовой или линейной функции с Sзад(t) – заданная форма импульса. Н-р для прямоугольного импульса:
В таком случае формирующая цепь представляется линейным звеном с передаточной функцией.
В случае ШИМ модулирования формирующая цепь – нелинейное звено, поскольку параметр С целью выявления этой специфики, рассмотрим свойства идеального импульсного элемента.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 834; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.43 (0.006 с.) |




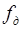 ;
; .
.

 - это решетчатая функция, порождаемая непрерывной X(t).
- это решетчатая функция, порождаемая непрерывной X(t).

 ;
;  - const.
- const.
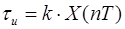

 - const.
- const.




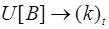 ,
, и высокой частоте дискретизации.
и высокой частоте дискретизации.

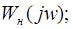
 ; и т.д.
; и т.д. , с постоянной частотой дискретизации
, с постоянной частотой дискретизации 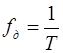 , где T – период дискретизации.
, где T – период дискретизации.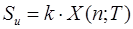
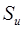 - ширина, фаза, амплитуда импульсной последовательности
- ширина, фаза, амплитуда импульсной последовательности 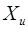 .
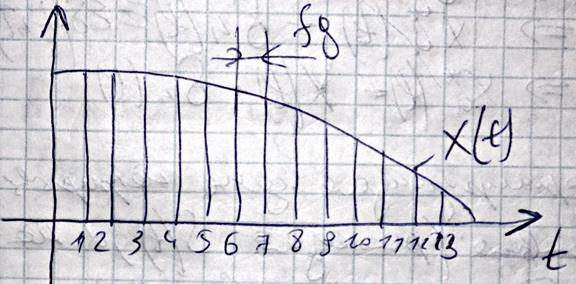
.
 , где n-номер дискрета (такта дискретизации).
, где n-номер дискрета (такта дискретизации).









 в
в  - зависит от величины входного сигнала. Во всех случаях формирующую цепь можно отнести к НЧ системе и в анализе специфики не рассматривать квантование.
- зависит от величины входного сигнала. Во всех случаях формирующую цепь можно отнести к НЧ системе и в анализе специфики не рассматривать квантование.


