
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изодромное корректирующее устройствоСодержание книги
Поиск на нашем сайте
Полученная частотная характеристика позволяет сделать вывод, что за счет подъема в области низких частот, как и в случае введения интегрирующего устройства, повышается надежность в установившемся режиме. Частотная характеристика в области высоких частот остается без изменений в следствии чего сохраняются остальные показатели качества. Быстродействие без ущерба устойчивости. Это стало возможным за счет того что ведется управление по величине ошибки и по интегралу от ошибки. Параллельные корректирующие устройства Параллельные корректирующие устройства подключаются к САУ параллельно корректируемому звену. Возможны 2 схемы: 1. Коррекция с помощью параллельной положительной связи
где
2. Коррекция с помощью отрицательной обратной связи
КОРРЕКЦИЯ ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ
Схема коррекции по задающему воздействию
Передаточная функция по задающему воздействию:
где W0(p) – исходное звено Wk(p) – корректирующее
Главная передаточная функция замкнутой САУ по задающему воздействию:
Для полной компенсации ошибки (для полной инвариантности) Такой случай возможен при
Не всегда возможно аппаратно создать КУ, с ПФ удовлетворяющему условию выше, связи с этим достигается неполная инвариантность (не выполняется когда, w0=1/p) однако для выполнения поставленных задач этого достаточно.
КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПО ВОЗМУЩАЮЩЕМУ ВОЗДЕЙСТВИЮ В реальной САУ возмущающее воздействие прикладывается к её определённой части. Структурная схема:
Корректирующее устройство в такую цепь вводят следующим образом.
Опишем передаточную функцию замкнутой САУ по возмущению
Условие при котором возмущение уничтожается:
При таком условии влияние f уничтожается уже на входе в звено W2. В данном случае также можно ограничиться не полной инвариантностью, если полная инвариантность вызывает технические трудности в реализации Wk. НЕЕДИНИЧНАЯ ОБРАТНАЯ СВЯЗЬ
Схема корректирующего устройства с неединичной обратной связью
В реализации такого корректирующего устройства возникают те же трудности что и для корректирующего устройства по задающему воздействию. На практике часто используют
Неединичная обратная связь так же позволяет обеспечить астатизм системы относительно задающего воздействия. В системе без интегрирующих звеньев соответствующим выбором коэффициента основной и обратной связи может быть обеспечен астатизм относительно задающего воздействия. Как и в предыдущем случае нестабильность коэффициентов К может служить причиной появления статической ошибки слежения.
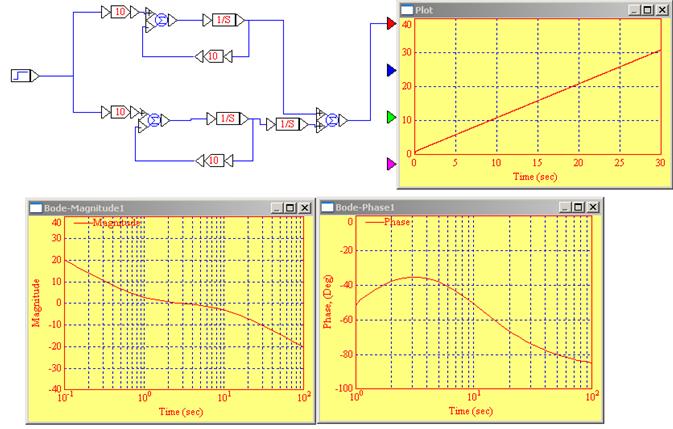
Частотный метод синтеза КУ. Параллельное соединение реального интегрирующего и апериодического 1-го порядка
Дано: k = 1; T = 0,1; Передаточная функция незамкнутой САУ:
ЛАЧХ ЛФЧХ - Время переходного процесса 0,1 с; - Перерегулирование 30%. - Точность 5%. Исходя из требований тонности и качества переходного процесса построим желаемую ЛАЧХ разомкнутой САУ. Определим начало желаемой ЛАЧХ: Кж= График желаемой ЛАЧХ будет начинаться в точке 20lg(Кж)= 20lg(20)=26 дБ. По заданному значению длительности переходного процесса, использую известное соотношение, определим частоту среза ωс.
Выбираем желаемую частоту среза ωс=60 рад/с, строим характеристику с наклоном -20 дБ. Низко- и среднечастотную составляющие соединяем прямой с наклоном 0 дБ. 2). Сравним желаемую ЛАЧХ с имеющейся, найдем их разность. В результате получим частотную характеристику последовательного корректирующего устройства, представленную на рисунке 1.
ЛАЧХ корректирующего устройства будет начинаться в точке 20lg(Kк)= =20lg(20)= 26,02 дБ. Передаточная функция корректирующего устройства будет иметь вид:
САУ после коррекции показана на рисунке 2.
Рисунок 1 – Частотные характеристики
ЛАЧХ ЛФЧХ ωср = 126; ωкр=∞
- время окончания переходного процесса:
- график амплитуды начинается в - перерегулирование - статическая ошибка
Точность САУ Методика даёт общее решение вопросам о влиянии изменения данных параметров на устойчивость САУ. Используется характеристическое уравнение САУ в такой форме:
Заменим p на j(w) и перейдём к частотной форме записи:
Представим в виде суммы двух слагаемых:
где Рассмотрим построение области устойчивости в плоскости одного комплексного параметра (например влияния
Заменяем p на jw:
Выражаем
Это выражение как и предыдущее уравнения будет состоять из двух частей. Здесь как и в предыдущих случаях (используя критерий Михайлова) можем построить границу D-разбиения:
Изменяя w от 0 до Граница D – разбиения – геометрическое расположение мнимой оси в плоскости одного параметра, переход означает переход через мнимую ось. В большинстве случаев интересует граница D – разбиения только на действительной оси, т.к. в большинстве случаев К и Т действительного числа, но в общем случае может быть и комплексные. Поскольку
Дискретные САУ
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.133.39 (0.009 с.) |






 –передаточная функция корректирующего устройства
–передаточная функция корректирующего устройства – передаточная функция параллельного корректирующего устройства;
– передаточная функция параллельного корректирующего устройства; – исходное корректируемое звено
– исходное корректируемое звено

 –передаточная функция корректирующего устройства
–передаточная функция корректирующего устройства – передаточная функция параллельного корректирующего устройства;
– передаточная функция параллельного корректирующего устройства;













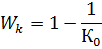


 , отсюда,
, отсюда, ;
; 
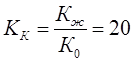




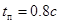


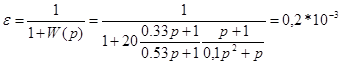
 (1)
(1)

 - исследуемые параметры (комбинации К и Т).
- исследуемые параметры (комбинации К и Т). ) тогда уравнение (1) может быть представлено в виде суммы двух слагаемых:
) тогда уравнение (1) может быть представлено в виде суммы двух слагаемых:


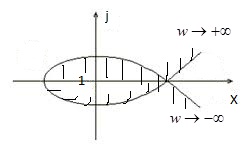
 находим X и Y и строим границу D – разбиения.
находим X и Y и строим границу D – разбиения.



