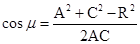Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий устойчивости Михайлова .Содержание книги
Поиск на нашем сайте
Критерий Михайлова предполагает построение годографа на комплексной плоскости. Для построения годографа из уравнения (4.1) путем подстановки S=jw получают аналитическое выражение вектора D(jw):
Уравнение (4.2) является комплексным и может быть представлено в виде:
где
Построение годографа производится по уравнению вектора D(jw) при изменении частою от 0 до ¥. Для случая устойчивости системы n-го порядка необходимо и достаточно, чтобы при w = 0 годограф начинался на вещественной положительной оси и обходил против часовой стрелки n квадрантов, нигде не обращаясь в нуль. Если годограф начинается в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной. 2. Критерий устойчивости Найквиста. (Подробно не только по ЛЧХ)
Критерий устойчивости Раусса-Гурвица.
Принцип аргумента. Запишем характеристический полином САУ в виде D(p) = a0(p - p1)(p - p2)...(p - pn) = 0. Его корни pi = i + ji = |pi|ejarg(pi), где arg(pi) = arctg(i/ai) + k, Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - pi изобразится разностью векторов (рис.68б), где p - любое число. Еcли менять значение p произвольным образом, то конец вектора p - pi будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как pi - это конкретное неизменное значение. В частном случае, если на вход системы подавать гармонические колебания с различной частотой, то p = j, а характеристический полином принимает вид: D(j) = a0(j - p1)(j - p2)...(j - pn). При этом концы векторов j - pi будут находиться на мнимой оси (рис.68в). Если менять от - до +, то каждый вектор j - pi будет поворачиваться относительно своего начала pi на угол +p для левых и - p для правых корней (рис.68г). Характеристический полином можно представить в виде D(j) = |D(j)|ejarg(D(j)), где |D(j)| = a0|j - p1||j - p2|...|j - pn|, arg(D(j)) = arg(j - p1) + arg(j - p2) +.. + arg(j - pn). Пусть из n корней m - правые, а n - m - левые, тогда угол поворота вектора D(j) при изменении от - до + равен = (n - m) - m, или при изменении от 0 до + получаем = (n - 2m)(/2). Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты от - до + равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на, а при изменении частоты от 0 до + эта разность умножается на /2. 5. Разложение в ряд Тейлора функции одной и нескольких переменных. Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Пусть функция
называется рядом Тейлора функции Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Теорема:
Для разложения в ряд Тейлора функции
Тогда разложение функции в ряд Тейлора по степеням
где Пример разложения в ряд Тейлора функции большого числа переменных Найдём выражение для разложения в ряд Тейлора функции трёх переменных. Для простоты обозначим переменные x, y и z, разложение проведём в окрестностях точки (0, 0, 0) и возьмём члены порядка не более второго. Оператор T будет иметь вид
Разложение в ряд Тейлора запишется в виде
Учитывая, что
получим
5. Устойчивость по Ляпунову Формулировка понятия устойчивости по Ляпунову. Невозмущенное движение (установившийся процесс) называется устойчивым, если при заданной сколь угодно малой области
В аналитической записи формулировка понятия устойчивости по Ляпунову будет следующей. Невозмущенное движение (установившийся процесс) будет устойчивым, если при заданных положительных сколь угодно малых числах
решение дифференциальных уравнений возмущенного движения (переходного процесса) удовлетворяет неравенствам
при любом сколь угодно большом t, начиная с некоторого Представим себе для этой аналитической записи геометрический образ в фазовом пространстве. Очевидно, что при ограничении начальных условий по каждой координате неравенствами (16.22) получается n-мерный параллелепипед со сторонами
Качество регулирования Качество работы любой системы регулирования в конечном счете определяется величиной ошибки, равной разности между требуемым и действительным значениями регулируемой величины: Знание мгновенного значения ошибки в течение всего времени работы регулируемого объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако в действительности, вследствие случайности задающего и возмущающего воздействий, такой подход не может быть реализован. Поэтому приходится оценивать качество системы регулирования по некоторым ее свойствам, проявляющимся при различных типовых воздействиях. Для определения качественных показателей системы регулирования в этом случае используются так называемые критерии качества. В настоящее время разработано большое число различных критериев качества систем регулирования. Все их можно разбить на четыре группы. К первой группе относятся критерии, в той или иной степени использующие для оценки качества величину ошибки в различных типовых режимах. Эту группу назовем критериями точности систем регулирования. Ко второй группе относятся критерии, определяющие величину запаса устойчивости, т. е. критерии, устанавливающие, насколько далеко от границы устойчивости находится система регулирования. Почти всегда опасной для системы является колебательная граница устойчивости. Это определяется тем, что стремление повысить общий коэффициент усиления в системе, как правило, приводит к приближению системы именно к колебательной границе устойчивости и затем — к возникновению незатухающих автоколебаний. Третья группа критериев качества определяет так называемое быстродействие систем регулирования. Под быстродействием понимается быстрота реагирования системы регулирования на появление задающих и возмущающих воздействий. Наиболее просто быстродействие может оцениваться по времени затухания переходного процесса системы. К четвертой группе критериев качества относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости и быстродействие. Обычно это делается при помощи рассмотрения некоторых интегральных свойств кривой переходного процесса. При рассмотрении понятий запаса устойчивости и быстродействия можно исходить из двух существующих в настоящее время точек зрения. Во-первых, можно основываться на характере протекания процессов во времени и использовать для формирования критериев качества переходную или весовую функцию, расположение полюсов и нулей передаточной функции замкнутой системы и т. п. Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и др. Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот и другой подход требует изучения условий эксплуатации построенных систем автоматического регулирования, так как только на основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем. Связь между временными и частотными свойствами системы автоматического регулирования имеет сложный характер и может быть определена в общем виде только в простейших случаях, например для систем, описываемых дифференциальным уравнением второго порядка. Однако отсутствие зависимостей, связывающих в общей форме свойства системы во временном и частотном представлениях, не может служить препятствием для развития и независимого использования критериев качества того или иного направления. Использование того или иного подхода при формулировании критериев качества определяется в настоящее время удобствами его применения в системах конкретного вида, а также, в известной мере, сложившимися в данной области традициями, Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и др. Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот и другой подход требует изучения условий эксплуатации построенных систем автоматического регулирования, так как только на основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем. Связь между временными и частотными свойствами системы автоматического регулирования имеет сложный характер и может быть определена в общем виде только в простейших случаях, например для систем, описываемых дифференциальным уравнением второго порядка. Однако отсутствие зависимостей, связывающих в общей форме свойства системы во временном и частотном представлениях, не может служить препятствием для развития и независимого использования критериев качества того или иного направления. Использование того или иного подхода при формулировании критериев качества определяется в настоящее время удобствами его применения в системах конкретного вида, а также, в известной мере, сложившимися в данной области традициями.
3.1(б) Приближенная оценка вида переходного процесса по вещественной частотной характеристике Построение кривой переходного процесса является в большинстве случаев весьма трудоемкой операцией. Поэтому целесообразно использовать методы, позволяющие определить вид переходной характеристики без построения всей кривой процесса. Это можно сделать по вещественной частотной характеристике Р ( Использование оценки вида переходного процесса по вещественной частотной характеристике наиболее удобно применять в том случае, когда для исследования автоматической системы используются частотные методы.
Интервал частот Заметим, что отбрасываемый «хвост» вещественной частотной характеристики ( На основании анализа интеграла (7.53) были получены следующие оценки качества переходного процесса. 1. Статическое отклонение 2. Чтобы величина перерегулирования 3. Для монотонности переходного процесса у(t) достаточно, чтобы 4. Простейшим признаком немонотонности переходного процесса является наличие значений например, если 5. В случае, если вещественная частотная характеристика
разность двух положительных невозрастающих непрерывных функций, то величина перерегулирования 6. Для монотонных процессов у(t) время затухания t1 до значения у=5% от статического отклонения
положительности вещественной частотной характеристики 7. Если заданную вещественную частотную характеристику
3.2 Частотные показатели и оценки качества 8,9 Частотные критерии качества Под частотными критериями качества будем понимать такие критерии, которые не рассматривают вида переходного процесса, а базируются на некоторых частотных свойствах системы. Частотные критерии качества особенно удобно применять при использовании частотных методов расчета, так как при этом получается наиболее простое решение задачи.
Частотные критерии наиболее разработаны в отношении оценки запаса устойчивости. Запас устойчивости можно определять по удалению амплитудно-фазовой характеристики разомкнутой системы (рис. 8.24, а) от точки Для общего случая условной устойчивости, изображенного на рис. 8.24,а, запас устойчивости по амплитуде определяется двумя точками а и с, и, соответственно, двумя величинами, выраженными обычно в децибелах:
Запас устойчивости по амплитуде тем больше, чем больше В случае абсолютной устойчивости смысл имеет только величина Запасом устойчивости по фазе называется запас по фазе где
сдвиг по фазе
В хорошо демпфированных системах запас по фазе составляет около 30–60°.
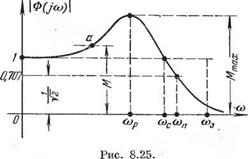
Недостатком рассмотренного критерия является то, что для определения запаса устойчивости необходимо задать два числа: В этом отношении более удобно определять запас устойчивости по показателю колебательности. Показателем колебательности называется максимальное значение ординаты Mmах амплитудной характеристики замкнутой системы (см. рис. 8.25) при начальной ординате, равной единице, т. е. относительная высота резонансного пика. Физически эта характеристика представляет собой следующее. Если управляющий сигнал на входе системы регулирования меняется по закону
где Максимальное значение этого модуля и представляет собой показатель колебательности (имеется в виду наибольший максимум)
Как видно из этих рассуждений, показатель колебательности определяется посредством задания задающего воздействия Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Допустимое значение показателя колебательности определяется на основании опыта эксплуатации систем регулирования. Считается, что в хорошо демпфированных системах регулирования показатель колебательности не должен превосходить значений 1,1–1,5, хотя в некоторых случаях можно допускать величины до 2–2,5. Для отыскания показателя колебательности системы регулирования нет необходимости строить амплитудную частотную характеристику (рис. 8.25) или отыскивать максимум (8.82). Существуют приемы, позволяющие найти показатель колебательности по виду амплитудно-фазовой характеристики разомкнутой системы. Возьмем на амплитудной характеристике (рис. 8.25) некоторую точку а, которой соответствует ордината М, и отобразим эту точку на комплексную плоскость частотной передаточной функции разомкнутой системы. Для этого рассмотрим уравнение
Сделаем подстановки
Возводя в квадрат правую и левую части и освобождаясь от знаменателя, после алгебраических преобразований получим
Это есть уравнение окружности с радиусом R и с центром, смещенным влево от начала координат на величину С. Задаваясь различными значениями М от 1 до значение ординаты амплитудной частотной характеристики. При М=1 окружность вырождается в прямую линию, параллельную оси ординат и проходящую слева от нее на расстоянии 0,5. При Для значений ординат амплитудной характеристики, лежащих в пределах
определяемое по наименьшей окружности М=const, которой коснется амплитудно-фазовая характеристика. Если при проектировании системы ставится условия, чтобы ее показатель колебательности был не больше некоторого заданного значения, например Мmax=1,5, то для выполнения этого необходимо, чтобы амплитуднофазовая характеристика не заходила внутрь окружности, соответствующей этому значению М (рис. 8.27). Амплитудно-фазовая характеристика может только коснуться этой окружности. В этом случае показатель колебательности будет как раз равен заданному значению Мmax. Таким образом, окружность Мтях является запретной зоной для амплитудно-фазовой характеристики разомкнутой системы. Эта зона охватывает точку
окружность заданного показателя колебательности (рис. 8.28). На окружности возьмем произвольную точку В и построим вектор, соединяющий эту точку с началом координат. Установим для этого вектора связь между его модулем А и запасом по фазе
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.192 (0.011 с.) |

 (4.2)
(4.2)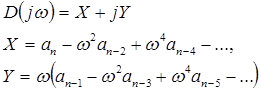






 бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд
. Формальный ряд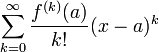
 в точке
в точке  производную в некоторой окрестности точки
производную в некоторой окрестности точки 

 — произвольное положительное число,
— произвольное положительное число,  точка
точка  при
при 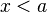 или
или  при
при  :
:

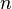 переменных
переменных  , которая в некоторой окрестности точки
, которая в некоторой окрестности точки  имеет полные производные вплоть до
имеет полные производные вплоть до 
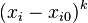 в окрестности точки
в окрестности точки 
 — n-ый член ряда.
— n-ый член ряда.





 ,
,
 (рис. 16.7, б) можно найти такую область
(рис. 16.7, б) можно найти такую область 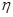 , что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области
, что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области 
 можно найти такие положительные числа
можно найти такие положительные числа  (i = 1,.. п), что при начальных условиях
(i = 1,.. п), что при начальных условиях (i = 1,.. п) (16.22)
(i = 1,.. п) (16.22) (i = 1,.. п)
(i = 1,.. п) .
. , внутри которого должна лежать начальная точка фазовой траектории М0 (x10, х20,.. хп0). На фазовой плоскости (
, внутри которого должна лежать начальная точка фазовой траектории М0 (x10, х20,.. хп0). На фазовой плоскости ( ) он обращается в прямоугольник. Аналогично и второе из написанных неравенств геометрически означает, что фазовые траектории не должны выходить из параллелепипеда со сторонами
) он обращается в прямоугольник. Аналогично и второе из написанных неравенств геометрически означает, что фазовые траектории не должны выходить из параллелепипеда со сторонами  .
. . В системах стабилизации при
. В системах стабилизации при 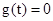 ошибка
ошибка  .
. ) замкнутой системы, которая используется для построения переходной функции. При этом предполагается, что переходный процесс у(t) вызван скачком задающего воздействия g(t). Возможна оценка вида переходного процесса при приложении скачка возмущения
) замкнутой системы, которая используется для построения переходной функции. При этом предполагается, что переходный процесс у(t) вызван скачком задающего воздействия g(t). Возможна оценка вида переходного процесса при приложении скачка возмущения  . В этом случае необходимо использовать вещественную часть частотной передаточной функции системы по возмущающему воздействию
. В этом случае необходимо использовать вещественную часть частотной передаточной функции системы по возмущающему воздействию  .
.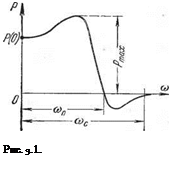 Пусть вещественная частотная характеристика замкнутой системы имеет вид, изображенный на рис. 3.1.
Пусть вещественная частотная характеристика замкнутой системы имеет вид, изображенный на рис. 3.1. , в котором
, в котором  , называется интервалом положительности. Интервал частот
, называется интервалом положительности. Интервал частот 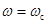 и далее при
и далее при  величина
величина  становится и остается меньше некоторой заданной достаточно малой положительной величины
становится и остается меньше некоторой заданной достаточно малой положительной величины  , влиянием остальной части вещественной частотной характеристики (при
, влиянием остальной части вещественной частотной характеристики (при 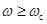 ) на качество переходного процесса можно пренебречь. Если же при
) на качество переходного процесса можно пренебречь. Если же при  оказывается, что
оказывается, что  , то при оценке качества переходного процесса в первом приближении можно принимать во внимание только интервал положительности
, то при оценке качества переходного процесса в первом приближении можно принимать во внимание только интервал положительности  регулируемой величины, получающееся в результате единичного скачка внешнего воздействия, равно начальному значению вещественной частотной характеристики Р(0). Если речь идет о скачке задающего воздействия, то Р(0) должно равняться либо 1, либо некоторому к0, если система должна воспроизводить задающее воздействие в определенном масштабе к0. Если же вводится скачок возмущающего воздействия f, то значение PF(0) должно быть как можно меньше, причем в астатической системе возможно PF (0) = 0.
регулируемой величины, получающееся в результате единичного скачка внешнего воздействия, равно начальному значению вещественной частотной характеристики Р(0). Если речь идет о скачке задающего воздействия, то Р(0) должно равняться либо 1, либо некоторому к0, если система должна воспроизводить задающее воздействие в определенном масштабе к0. Если же вводится скачок возмущающего воздействия f, то значение PF(0) должно быть как можно меньше, причем в астатической системе возможно PF (0) = 0. не превышала 18% от статического отклонения, достаточно иметь положительную невозрастающую непрерывную характеристику
не превышала 18% от статического отклонения, достаточно иметь положительную невозрастающую непрерывную характеристику  .
. представляла собой отрицательную, убывающую по модулю непрерывную функцию от
представляла собой отрицательную, убывающую по модулю непрерывную функцию от  .
. (кривая 3 на рис. 8.7, б). Переходный процесс тоже будет немонотонным, когда кривая
(кривая 3 на рис. 8.7, б). Переходный процесс тоже будет немонотонным, когда кривая  (рис. 8.7, в), причем где через обозначены целочисленные значения, взятые с избытком;
(рис. 8.7, в), причем где через обозначены целочисленные значения, взятые с избытком; , то берется
, то берется 
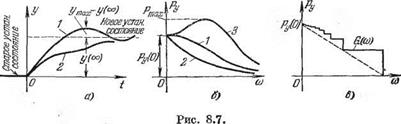
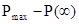 .
. . В общем же случае
. В общем же случае  . Вообще при прочих равных условиях переходный процесс тем быстрее затухает, чем больше
. Вообще при прочих равных условиях переходный процесс тем быстрее затухает, чем больше  т. е. чем больше растянута область
т. е. чем больше растянута область
 и
и  .
.
 . Для этой цели вводятся понятия запаса устойчивости по амплитуде (модулю) и запаса устойчивости по фазе.
. Для этой цели вводятся понятия запаса устойчивости по амплитуде (модулю) и запаса устойчивости по фазе. ,
,  .
. и
и  . В хорошо демпфированных системах эти величины составляют примерно 6–20 дб, что соответствует 2–10 в линейном масштабе.
. В хорошо демпфированных системах эти величины составляют примерно 6–20 дб, что соответствует 2–10 в линейном масштабе. .
. ,
, – аргумент частотной передаточной функции разомкнутой системы, соответствующий модулю, равному единице (точка b на рис. 8.24, а):
– аргумент частотной передаточной функции разомкнутой системы, соответствующий модулю, равному единице (точка b на рис. 8.24, а):
 определяется условием
определяется условием
 В некоторых случаях вместо задания дискретных точек, определяющих запас устойчивости системы регулирования (точки а, b и с на рис. 8.24, а), задают некоторую запретную область для амплитудно-фазовой характеристики разомкнутой системы. Эта запретная область окружает точку
В некоторых случаях вместо задания дискретных точек, определяющих запас устойчивости системы регулирования (точки а, b и с на рис. 8.24, а), задают некоторую запретную область для амплитудно-фазовой характеристики разомкнутой системы. Эта запретная область окружает точку  и запаса устойчивости по модулю
и запаса устойчивости по модулю  (рис. 8.24, б).
(рис. 8.24, б). , то регулируемая величина в режиме установившихся вынужденных колебаний будет меняться по закону
, то регулируемая величина в режиме установившихся вынужденных колебаний будет меняться по закону  . Отношение амплитуд
. Отношение амплитуд  и
и  определяется модулем частотной передаточной функции замкнутой системы:
определяется модулем частотной передаточной функции замкнутой системы: (8.81)
(8.81) – частотная передаточная функция разомкнутой системы.
– частотная передаточная функция разомкнутой системы. (8.82)
(8.82) и отыскания относительной величины резонансного пика.
и отыскания относительной величины резонансного пика.
 и
и  , тогда
, тогда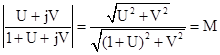
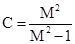 (8.84)
(8.84) (8.85)
(8.85) , можно построить ■семейство таких окружностей (рис. 8.26). На каждой окружности написано
, можно построить ■семейство таких окружностей (рис. 8.26). На каждой окружности написано окружность вырождается в точку, совпадающую с точкой
окружность вырождается в точку, совпадающую с точкой  , получается семейство окружностей, расположенных справа от линии М=1, симметрично с первым семейством. При М=0 окружность вырождается в точку, совпадающую с началом координат.
, получается семейство окружностей, расположенных справа от линии М=1, симметрично с первым семейством. При М=0 окружность вырождается в точку, совпадающую с началом координат. Для построения амплитудной характеристики (рис. 8.25) достаточно в тех же координатах, где построены окружности М=const, нанести амплитудно-фазовую характеристику разомкнутой системы. Точки пересечения этой характеристики с окружностями будут определять точки амплитудной характеристики с соответствующими значениями ординат, равными М. Для определения показателя колебательности можно не строить амплитудную характеристику, так как достаточно знать одно максимальное значение ординаты
Для построения амплитудной характеристики (рис. 8.25) достаточно в тех же координатах, где построены окружности М=const, нанести амплитудно-фазовую характеристику разомкнутой системы. Точки пересечения этой характеристики с окружностями будут определять точки амплитудной характеристики с соответствующими значениями ординат, равными М. Для определения показателя колебательности можно не строить амплитудную характеристику, так как достаточно знать одно максимальное значение ординаты  ,
,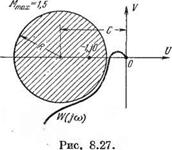 Величина показателя колебательности может быть определена и в случае использования логарифмических частотных характеристик. Для этого отобразим запретную эону (рис. 8.27) на логарифмическую сетку. Рассмотрим отдельно
Величина показателя колебательности может быть определена и в случае использования логарифмических частотных характеристик. Для этого отобразим запретную эону (рис. 8.27) на логарифмическую сетку. Рассмотрим отдельно
 . Из треугольника ОВО1 по теореме косинусов находим
. Из треугольника ОВО1 по теореме косинусов находим