
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства идеального импульсного элемента. Уравнения связи изображений входного и выходного сигналов идеального импульсного элемента. Спектральные (частотные) свойства ИИЭСодержание книги
Поиск на нашем сайте
Амплтудно-импульсный элемент реагирует на равноотстоящие друг от друга значения входного сигнала f(t) при t=nT. Его выходной сигнал fp*(t) является последовательностью импульсов определенной формы, амплитуда которых пропорциональна значениям f(nT) (см. рис.2.1).
Рис. 2.1. Входной и выходной сигналы амплитудно-импульсного элемента.
Другими словами, выход амплитудно-импульсного элемента (квантователя) fp*(t) представляет последовательность импульсов конечной длительности p, амплитуда которых промодулирована входным сигналом f(t) (см. рис. 2.2 и рис.2.3).
Рис. 2.2. Схема квантователя с постоянным периодом и конечным временем выборки
Рис. 2.3. Входной и выходной сигналы квантователя с постоянным периодом
Заметим, что в реальном импульсном элементе форма импульса квантователя может быть произвольной, не обязательно прямоугольной. От реального импульсного элемента удобно перейти к идеальному элементу. При этом реальный импульсный элемент может быть представлен как последовательное соединение идеального импульсного элемента и формирующей цепи, реакция которой на импульсное воздействие равна w(t). Частотная характеристика формирующей цепи и изображение её выходного сигнала обозначим соответственно W(jω) и W(s).
Рис. 2.4. Представление реального импульсного элемента как соединения идеального импульсного элемента и формирующей цепи.
Рассмотрим идеальный импульсный элемент. В соответствии с определением уравнение, связывающее входной x(t) и выходной
т.е. выходная переменная есть последовательность
т.е. преобразование Лапласа выходной величины ИИЭ равно дискретному преобразованию Лапласа решетчатой функцииx[nT]. Связь между изображениями непрерывной x(t) и решетчатой x[nT] функций устанавливается зависимостью
В итоге ИИЭ может быть описан зависимостями (2) или (3). Зависимость (2) устанавливает связь между входнойx(t) и выходной
Свойства: Идеальный импульсный элемент можно представить как квантователь с бесконечно малым временем выборки p, тогда выходной сигнал такого квантователя fp*(t) равен: fp*(t) = f(nT) при t = nT; fp*(t) = 0 при t = 0. (2.1) Последнее можно представить, как модуляцию несущего сигнала вида
входным сигналом f(t), где δ Т (t) представляет собой последовательность единичных импульсов (площадь которых равна единице), равноотстоящих по времени, начинающихся при минус бесконечности и продолжающихся до плюс бесконечности, как показано на рис. 2.6.
Рис. 2.6. Последовательность единичных импульсов
Выходной сигнал f*(t) идеального квантователя можно записать в форме
Предполагая, что квантование начинается с момента времени t = 0, можно получить выражение для преобразования Лапласа выходного сигнала квантователя.
В последнем выражении учитывается, что δ-функция всюду равна нулю, кроме точки t = kT. Кроме того, учитывая, что L{ δТ(t-kT)} = e-pkT получаем:
Последнее выражение называется также дискретным преобразованием Лапласа или D-преобразованием, поскольку в нём вместо непрерывных функций f(t) фигурируют решётчатые функции f(kT).
Подставим в (2.4) выражение δТ(t) через ряд Фурье; получим
На основании свойств преобразования Лапласа L{f(t)·ejkω0t} = F(s – jkω0). Таким образом,
Соотношение (2.6) устанавливает связь между изображениями непрерывной F(s) и решётчатой функций F*(s). Операцию нахождения F*(s) по изображению F(s) называют D-преобразованием. Выражение (2.6) имеет вид бесконечного ряда, откуда следует, что выходная величина импульсного элемента содержит высокочастотные составляющие. Предположим, что частотный спектр входной величины имеет вид, показанный на рис. 2.7а. В этом случае спектр выходного сигнала импульсного элемента содержит в себе спектр входной величины, а также составляющие других частот, как показано на рис. 2.7б. Этот рисунок соответствует случаю, когда частота самой высокочастотной составляющей входной величины меньше половины частоты квантования (ωс > ω0/2.)
Рис. 2.7. Амплитудные спектры входного и выходного сигналов идеального квантователя: а – амплитудный спектр непрерывного входного сигнала f(t); б – амплитудный спектр выходного сигнала (ω0 > 2 ωc).
Очевидно, что при таком выборе частоты квантования ω0 возможно (чисто теоретически) восстановить входной сигнал без всякого искажения. Если же частота повторения меньше удвоенной частоты самой высокочастотной составляющей входной величины, то выходная величина импульсного элемента искажается по отношению к входному сигналу (см. рис. 2.8).
а) б) Рис. 2.8. Амплитудные спектры входного и выходного сигналов идеального квантователя: а – амплитудный спектр непрерывного входного сигнала f(t); б – амплитудный спектр выходного сигнала (ω0 < 2 ωc).
Соответствующие временные зависимости входных и выходных сигналов импульсного элемента показаны на рис. 2.9.
Рис. 2.9. Входные и выходные сигналы идеального импульсного элемента: а – входной, б – выходной сигналы при ω0 > 2 ωc; в – входной, г – выходной сигналы при ω0 < 2 ωc. Условия эквивалентности преобразования информации в ИЭ. Теорема Котельникова.
В 1933 г. была опубликована работа В.А.Котельникова «О пропускной способности эфира и проволоки электросвязи» Материалы радиосекции к I Всесоюзному съезду по реконструкции связи, Всесоюзный энергетический комитет. В работе был сформулирован следующий фундаментальный вывод: Для восстановления входной величины частота повторения должна быть больше или равна частоте самой высокочастотной составляющей входной величины: ω0 / 2 ωc. (2.7) Теорема Котельникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит, что, если аналоговый сигнал
Если же условия теоремы Котельникова нарушаются и отсчеты во времени берутся недостаточно часто, то однозначное восстановление исходного сигнала принципиально невозможно. Через отсчетные точки можно провести бесчисленное множество кривых, спектральные плотности которых отличны от нуля вне полосы Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временной характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и обычно имеют разрывы во временной характеристике. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают два следствия: · Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой · Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.2.242 (0.008 с.) |





 сигналы ИИЭ, имеет вид
сигналы ИИЭ, имеет вид
 , (2)
, (2) -функций, промоделированных входным сигналом. При этом
-функций, промоделированных входным сигналом. При этом ,
, (3)
(3) (2.2)
(2.2)
 (2.3)
(2.3) (2.4)
(2.4)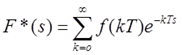 (2.5)
(2.5)
 (2.6)
(2.6)


 имеет конечный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с частотой, строго большей удвоенной верхней частоты
имеет конечный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с частотой, строго большей удвоенной верхней частоты  :
:



