
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема №4: устойчивость работы линейных сауСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
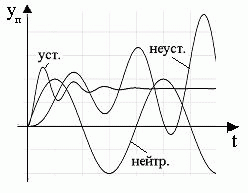
Понятие устойчивости является важнейшей качественной оценкой динамических свойств САР. Устойчивость САР связана с характером её поведения после прекращения внешнего воздействия, которое может быть оценено решением дифференциального уравнения, описывающего работу системы. Общая теория устойчивости разработана А.М. Ляпуновым. Линейная система называется устойчивой, если ее выходная координата остается ограниченной при любых ограниченных по абсолютной величине входных воздействиях. Устойчивость линейной системы определяется ее характеристиками и не зависит от действующих воздействий.
Пара мнимых корней (αi=0) характеристического уравнения позволяет получить переходную составляющую в виде автоколебаний с постоянной амплитудой:
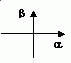
Полученные корни характеристического уравнения могут быть представлены в виде точек на комплексной плоскости (рис.4.2.).
Для устойчивых систем необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости корней. Если хотя бы один вещественный корень или пара комплексных сопряженных корней находится справа от мнимый оси, то система является неустойчивой. Если имеется нулевой корень или пара чисто мнимых корней, то система считается нейтральной (находящейся на границе устойчивости и неустойчивости). Таким образом, мнимая ось комплексной плоскости является границей устойчивости. С целью упрощения анализа устойчивости систем разработаны ряд специальных методов, которые получили название критерии устойчивости. Критерии устойчивости делятся на две разновидности: алгебраические (критерий Гурвица) и частотные (критерии Михайлова и Найквиста). Алгебраические критерии являются аналитическими, а частотные - графоаналитическими. Критерии устойчивости позволяют также оценить влияние параметров системы на устойчивость. © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Алгебраический критерий Гурвица находит широкое применение при анализе САР. Первоначально, из коэффициентов уравнения (4.1) составляется матрица главного определителя:
По диагонали матрицы от верхнего левого угла записываются по порядку все коэффициенты уравнения (4.1.), начиная с а1. Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз - уменьшались.
Последний определитель Гурвица, как видно из приведенной выше матрицы, равен Δn=an*Δn-1. Поэтому его положительность сводится при Δn-1>0 к условию an>0. Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов ai. Если определитель Δn=0, то система находится на границе устойчивости. Из условия Δn-1=0 можно определить параметры, при которых система находится на границе устойчивости, например, критический коэффициент усиления разомкнутой САУ Ккр. Пример задачи © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Критерий Михайлова предполагает построение годографа на комплексной плоскости. Для построения годографа из характеристического уравнения замкнутой системы (4.1) путем подстановки p=jω получают аналитическое выражение вектора M(jω):
Построение годографа производится по уравнению вектора M(jω) при изменении часты от 0 до +
где m - число правых корней характеристического полинома; n - порядок характеристического уравнения системы.
Имеется вторая формулировка критерия Михайлова: для устойчивости системы необходимо и достаточно, чтобы корни уравнений P(ω) = 0 и Q(ω) = 0 перемежались (чередовались), т.е. годограф последовательно пересекал оси комплексной плоскости. Этой формулировкой удобно пользоваться для исследования устойчивости систем до пятого порядка включительно. По уравнению (4.3) можно определить количество правых корней в неустойчивых системах. Пример задачи © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Критерий Найквиста - частотный критерий, позволяющий по виду амплитудно-фазовой частотной характеристики разомкнутой системы оценить устойчивость работы замкнутой системы. АФЧХ может быть получена экспериментально или аналитически. Аналитическое построение АФЧХ производится обычными методами. Критерий Найквиста формулируется по разному в зависимости от того, устойчива разомкнутая система или нет.
АФЧХ астатической системы, начинаясь на вещественной положительной полуоси, при ω->0 дугой бесконечно большого радиуса перемещается на угол, равный -ν
Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы охватывала точку с координатами (-1, j0) и при изменении частоты от 0 до
Запас устойчивости по фазе задается некоторым углом φ (рис.4.6). В хорошо демпфированных системах запас устойчивости по амплитуде составляет примерно 6-20 дБ, что составляет 2÷10 в линейном масштабе, а запас по фазе от 30 до 60°.
По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе φзап отсчитывается по л.ф.х. на частоте среза ωср и равен φзап=π - φ(ωср), а запас по амплитуде Lзап соответствует значению л.а.х. на частоте, при которой л.ф.х. равна -π (рис.4.7). Если φ(ωср)=-&pi, то система находится на границе устойчивости. Критический коэффициент усиления разомкнутой системы Kкр определяется из выражения 20*lg(Kкр)=20*lg(Kраз) + Lзап.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
При исследовании устойчивости большое прикладное значение имеет построение областей устойчивости в плоскости одного или каких-либо двух параметров, влияние которых на устойчивость исследуется. Уравнение границы устойчивости (D-разбиение) может быть получено из любого критерия устойчивости: D(jω,K,Ti)=0 - Михайлова или Δn-1= 0 - Гурвица. Однако на практике чаще применяют наиболее общий метод, предложенный Ю.И.Неймарком, и названный им методом D-разбиения. Кривая D-разбиения представляет собой отображение мнимой оси плоскости корней на плоскость интересующих нас параметров. Для этого характеристическое уравнение замкнутой системы представляется в виде:
Кривая D-разбиения по 1 параметру штрихуется одинарной штриховкой слева, если двигаться по границе устойчивости в направлении возрастания ω от -
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
П р и м е р: Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой П р и м е р: Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид
Р е ш е н и е. Из рисунка видно, что при изменении частоты от 0 до +ω суммарный угол поворота годографа Михайлова равен - © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
1. Дайте определение устойчивости системы с физической и математической точек зрения. © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |










 и т.д.
и т.д.
 . Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω<
. Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω< 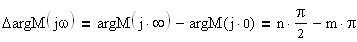 , (4.3)
, (4.3)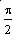 , так как m=0 для обеспечения устойчивости системы.
, так как m=0 для обеспечения устойчивости системы.




 .
.
 , тогда
, тогда 


 .
.
 . Откуда число положительных корней m = 2.
. Откуда число положительных корней m = 2.


